Mathematics
In the given circle with diameter AB, find the value of x.
Circles
19 Likes
Answer
As angles in same segment are equal.
∴ ∠ABD = ∠ACD = 30°.
From figure,
∠ADB = 90° [As angle in semi-circle is a right angle.]
In △ADB,
⇒ ∠ABD + ∠ADB + ∠BAD = 180° [By angle sum property of triangle]
⇒ 30° + 90° + x = 180°
⇒ 120° + x = 180°
⇒ x = 180° - 120° = 60°.
Hence, the value of x = 60°.
Answered By
10 Likes
Related Questions
O is the center of the circle, OB = BC and ∠BOC = 20°.
Statement (1) : x = 2 x 20° = 40°
Statement (2) : ∠BOC = 20°.
x = ∠OAB + 20° = ∠OBA + 20° = 40° + 20° = 60°
Both statements are true.
Both statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
O is the center of the circle and ∠AOC = 120°.
Statement (1) : ∠ABC = 120°
Statement (2) : ∠ABC + ∠ADC = 180° ⇒ ∠ABC + 60° = 180°.
Both statements are true.
Both statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
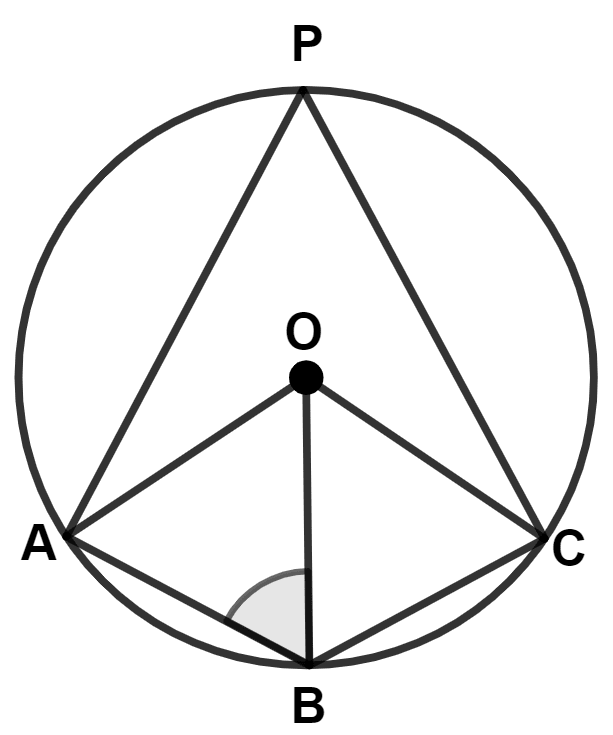
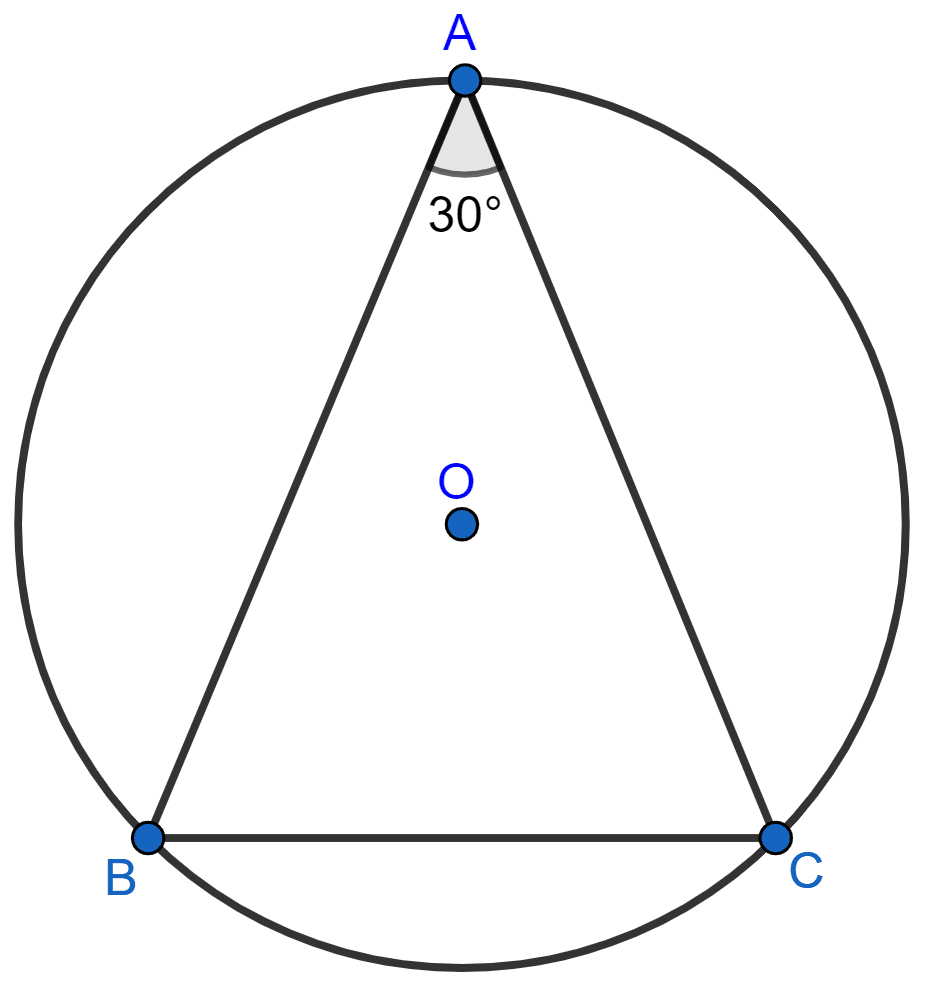
In the given figure, ABC is a triangle in which ∠BAC = 30°. Show that BC is equal to the radius of the circumcircle of the triangle ABC, whose centre is O.
Prove that the circle drawn on any one of the equal sides of an isosceles triangle as diameter bisects the base.