Mathematics
In the given figure, ABC is a triangle in which ∠BAC = 30°. Show that BC is equal to the radius of the circumcircle of the triangle ABC, whose centre is O.
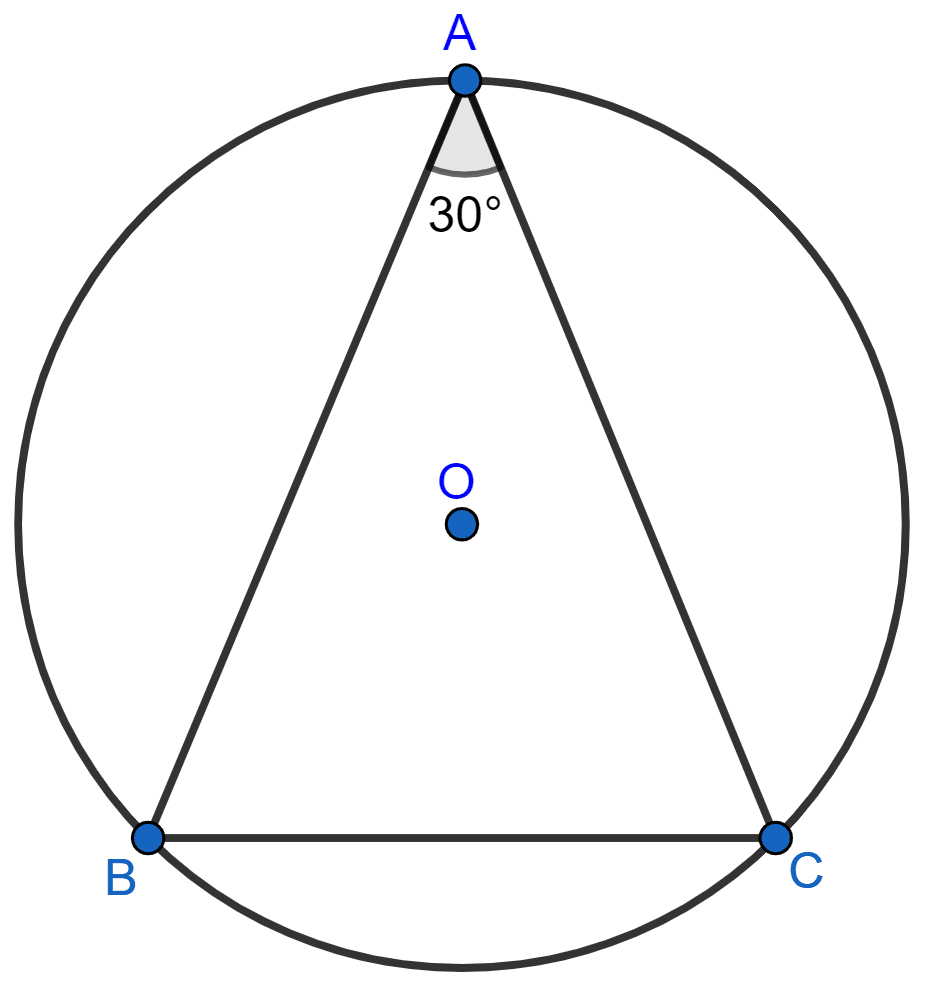
Circles
21 Likes
Answer
Join OB and OC.
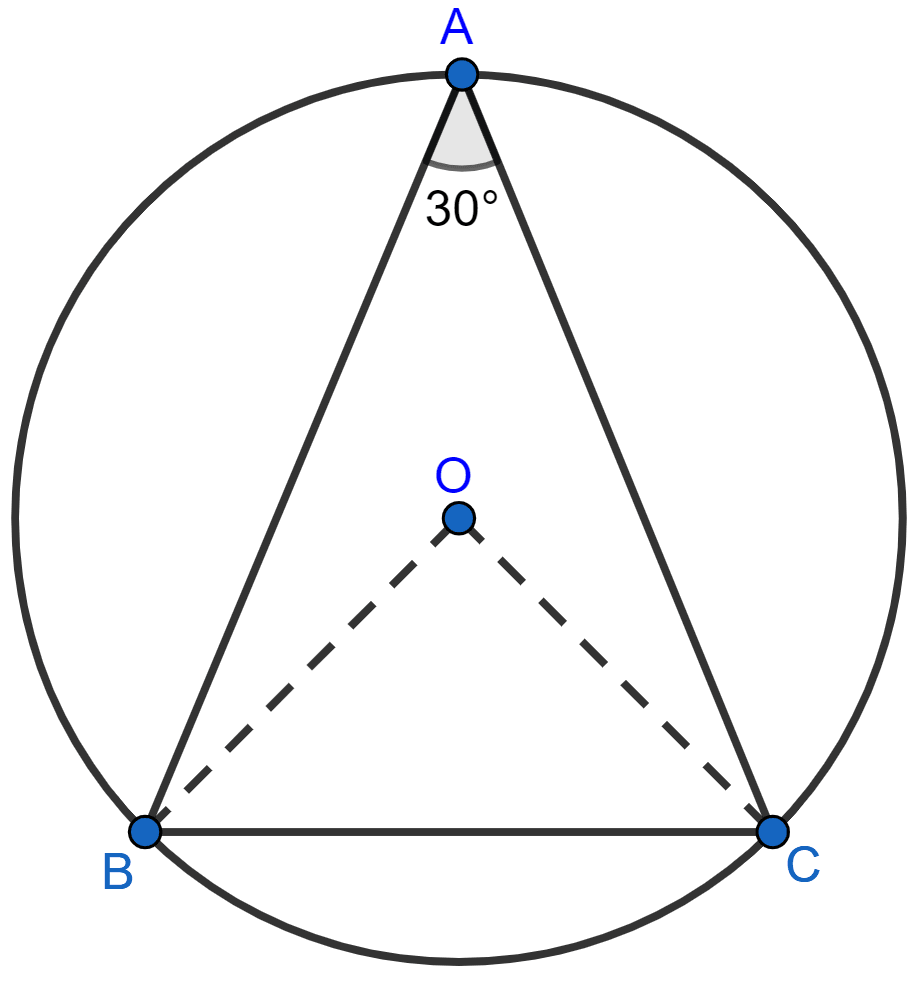
We know that,
Angle at the centre is twice the angle at remaining circumference.
∴ ∠BOC = 2∠BAC = 2 × 30° = 60°
In △OBC,
⇒ OB = OC [Radii of same circle]
⇒ ∠OBC = ∠OCB = x (let) [As angles opposite to equal sides are equal]
⇒ ∠BOC + ∠OBC + ∠OCB = 180°
⇒ 60° + x + x = 180°
⇒ 2x + 60° = 180°
⇒ 2x = 180° - 60°
⇒ 2x = 120°
⇒ x = = 60°.
∴ ∠OBC = ∠OCB = ∠BOC = 60°.
Hence, △OBC is an equilateral triangle.
∴ OB = OC = BC.
Hence, proved that BC is equal to the radius of the circumcircle of the triangle ABC.
Answered By
15 Likes
Related Questions
In the given figure, O is center of the circle. Chord BC = chord CD and angle A = 80°. Angle BOC is :
120°
80°
100°
160°

In the given circle with diameter AB, find the value of x.

Prove that the circle drawn on any one of the equal sides of an isosceles triangle as diameter bisects the base.
In the given figure, chord ED is parallel to diameter AC of the circle. Given ∠CBE = 65°, calculate ∠DEC.