Mathematics
Answer
We know that opposite sides of a rectangle are equal.
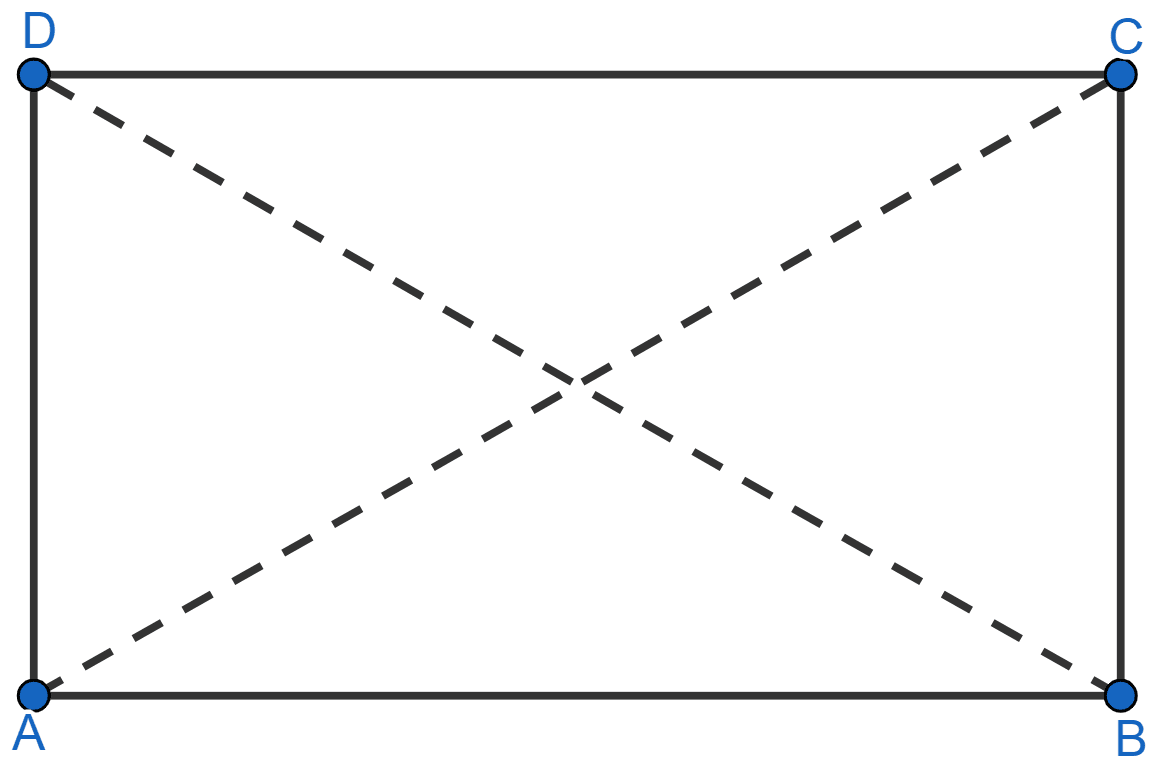
∴ AD = BC and AB = CD
Also, the diagonals of rectangle are equal.
∴ AC = BD
Now, consider ΔADC and ΔBCD
⇒ AD = BC
⇒ AC = BD
⇒ DC = DC [Common]
∴ ΔADC ≅ ΔBCD by SSS congruency rule.
∴ ∠ ADC = ∠BCD = x (let) [By C.P.C.T.]
But, adjacent sides of a parallelogram are supplementary. [∵ rectangle is a parallelogram].
∴ ∠ADC + ∠BCD = 180°
⇒ x + x = 180°
⇒ 2x = 180°
⇒ x = 90°
⇒ ∠ADC = ∠BCD = 90°.
Since, opposite angles of a parallelogram are also equal.
∴ ∠DAB = ∠BCD = 90° and ∠ABC = ∠ADC = 90°.
Hence, proved that each angle of a rectangle is 90°.
Related Questions
In figure (2) given below, ABCD is an isosceles trapezium. Find the values of x and y.

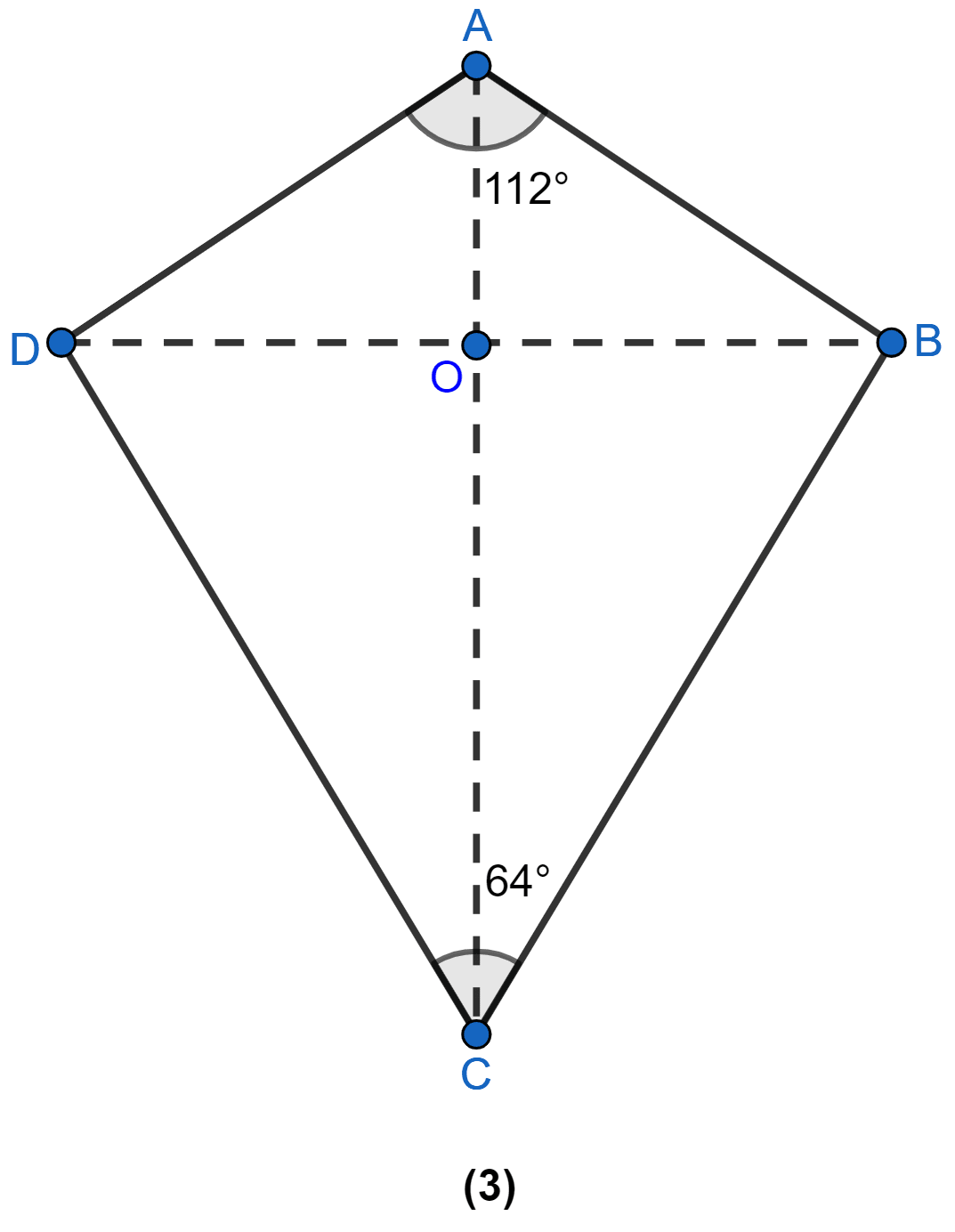
In figure (3) given below, ABCD is a kite and diagonals intersect at O. If ∠DAB = 112° and ∠DCB = 64°, find ∠ODC and ∠OBA.
If the angle of a quadrilateral are equal, prove that it is a rectangle.
If the diagonals of a rhombus are equal, prove that it is a square.