Mathematics
If the angle of a quadrilateral are equal, prove that it is a rectangle.
Rectilinear Figures
44 Likes
Answer
Suppose there is a quadrilateral ABCD.

Let ∠A = ∠B = ∠C = ∠D = x
So, ∠A = ∠C and ∠B = ∠D (Opposite angles are equal)
∴ ABCD is a parallelogram.
Since, sum of angles in a quadrilateral = 360°
⇒ ∠A + ∠B + ∠C + ∠D = 360°
⇒ x + x + x + x = 360°
⇒ 4x = 360°
x =
⇒ x = 90°.
∴ ∠A = ∠B = ∠C = ∠D = 90°.
Since, each angle = 90°,
Hence, proved that ABCD is a rectangle.
Answered By
29 Likes
Related Questions
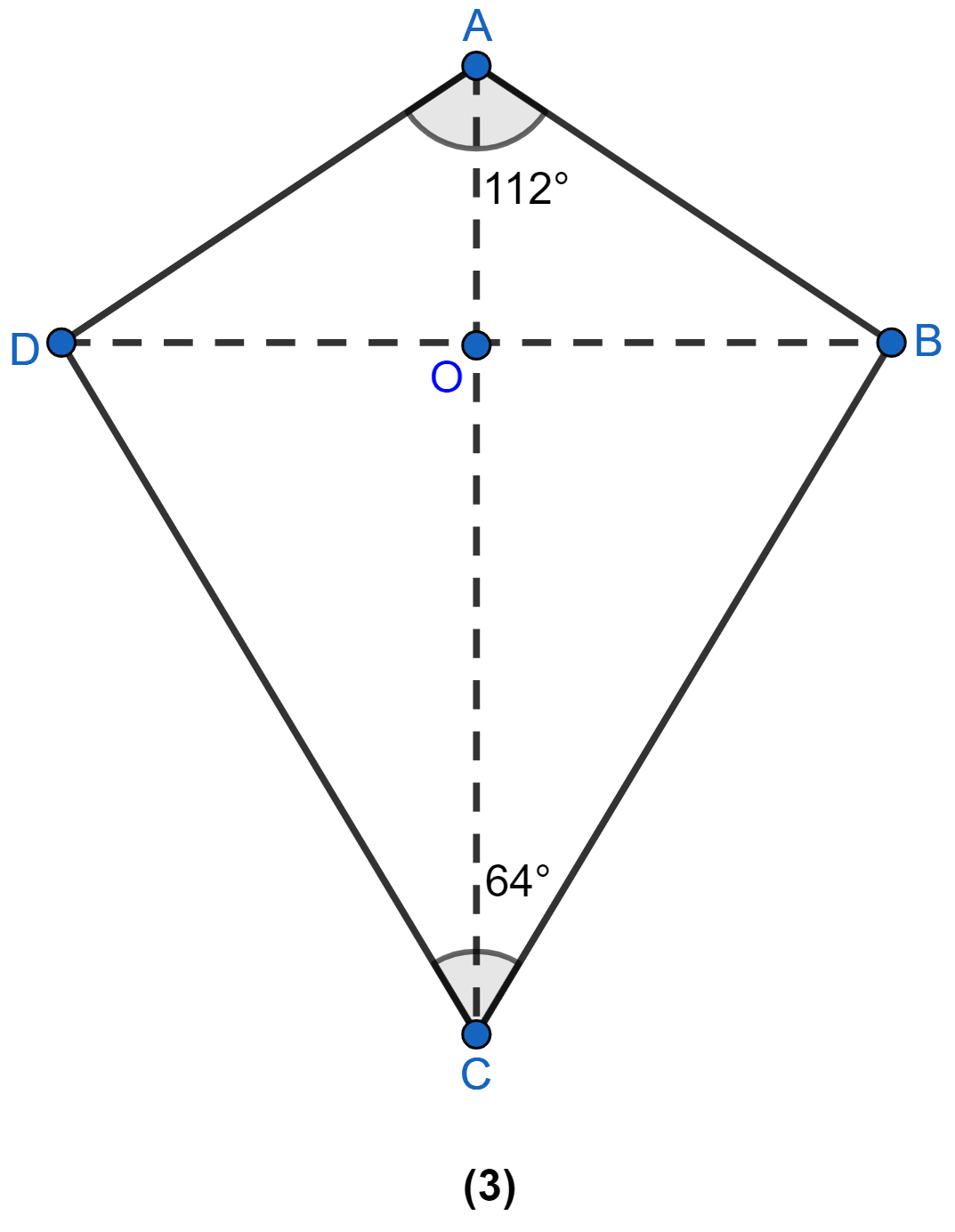
In figure (3) given below, ABCD is a kite and diagonals intersect at O. If ∠DAB = 112° and ∠DCB = 64°, find ∠ODC and ∠OBA.
Prove that each angle of a rectangle is 90°.
If the diagonals of a rhombus are equal, prove that it is a square.
Prove that every diagonal of a rhombus bisects the angles at the vertices.