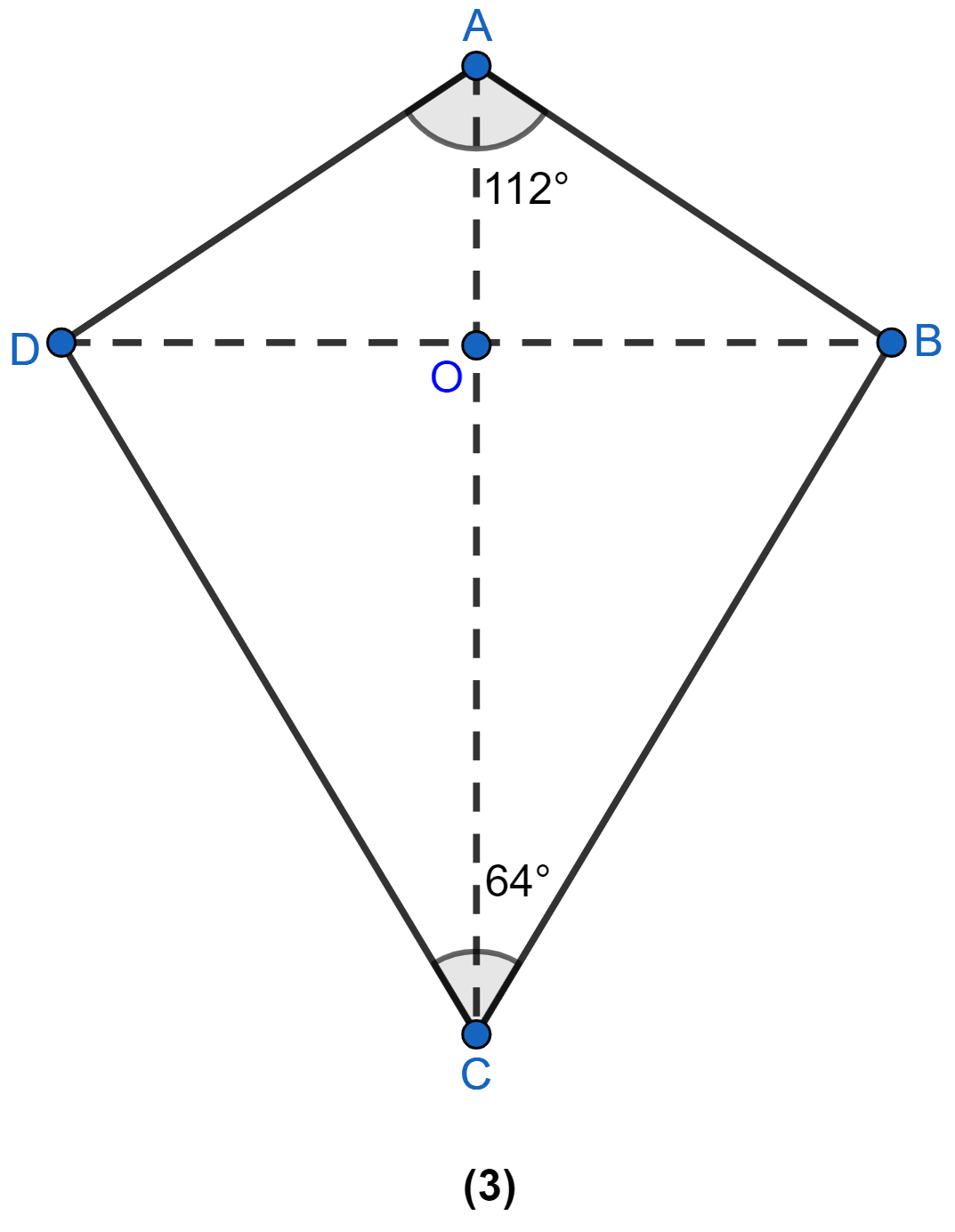
In figure (3) given below, ABCD is a kite and diagonals intersect at O. If ∠DAB = 112° and ∠DCB = 64°, find ∠ODC and ∠OBA.

Diagonals of a kite bisect the vertex angles.

∴ ∠OCD = $\dfrac{∠C}{2} = \dfrac{64}{2}$ = 32° and ∠OAB = $\dfrac{∠A}{2} = \dfrac{112}{2}$ = 56°

Diagonals of a kite are perpendicular to each other.

∴ ∠DOC = 90°

⇒ ∠OCD + ∠DOC + ∠ODC = 180°

⇒ 32° + 90° + ∠ODC = 180°

⇒ ∠ODC = 58°.

Diagonals of a kite are perpendicular to each other.

∴ ∠AOB = 90°

⇒ ∠AOB + ∠OAB + ∠OBA = 180°

⇒ 90° + 56° + ∠OBA = 180°

⇒ ∠OBA = 180° - 146° = 34°.

Hence, ∠OBA = 34° and ∠ODC = 58°.