Mathematics
In figure (1) given below, ABCD is a trapezium. Find the values of x and y.

Rectilinear Figures
44 Likes
Answer
Sum of adjacent co-interior angles of a trapezium = 180° (As AB || DC)
∴ ∠A + ∠D = 180°
⇒ x + 20° + 2x + 10° = 180°
⇒ 3x + 30° = 180°
⇒ 3x = 150°
⇒ x =
⇒ x = 50°.
∴ ∠B + ∠C = 180°
⇒ 92° + y = 180°
⇒ y = 180° - 92° = 88°.
Hence, x = 50° and y = 88°.
Answered By
29 Likes
Related Questions
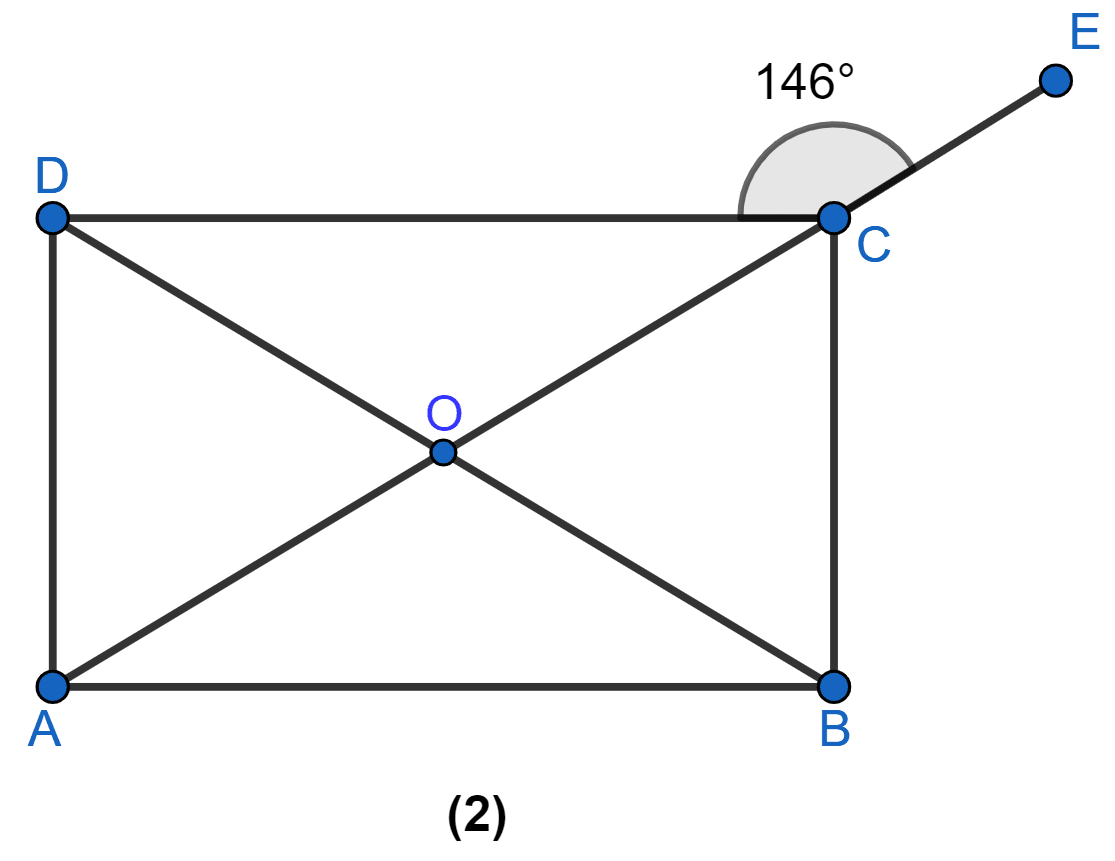
In Figure (2) given below, ABCD is a rectangle and diagonals intersect at O. AC is produced to E. If ∠ECD = 146°, find the angles of △AOB.
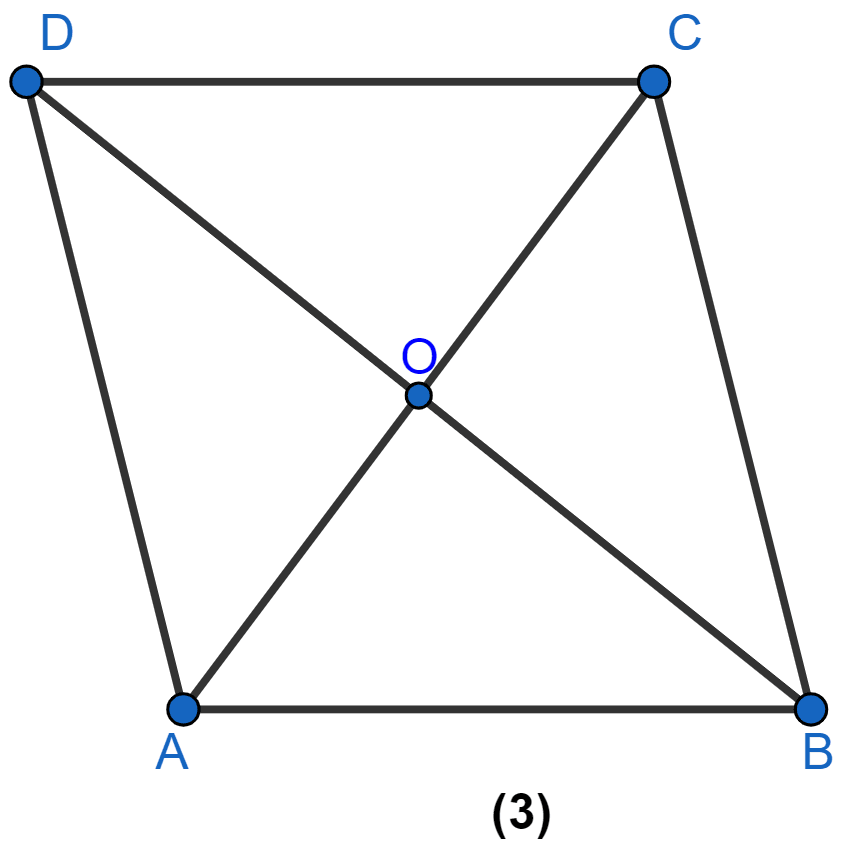
In figure (3) given below, ABCD is a rhombus and diagonals intersect at O. If ∠OAB : ∠OBA = 3 : 2, find the angles of the △AOD.
In figure (2) given below, ABCD is an isosceles trapezium. Find the values of x and y.

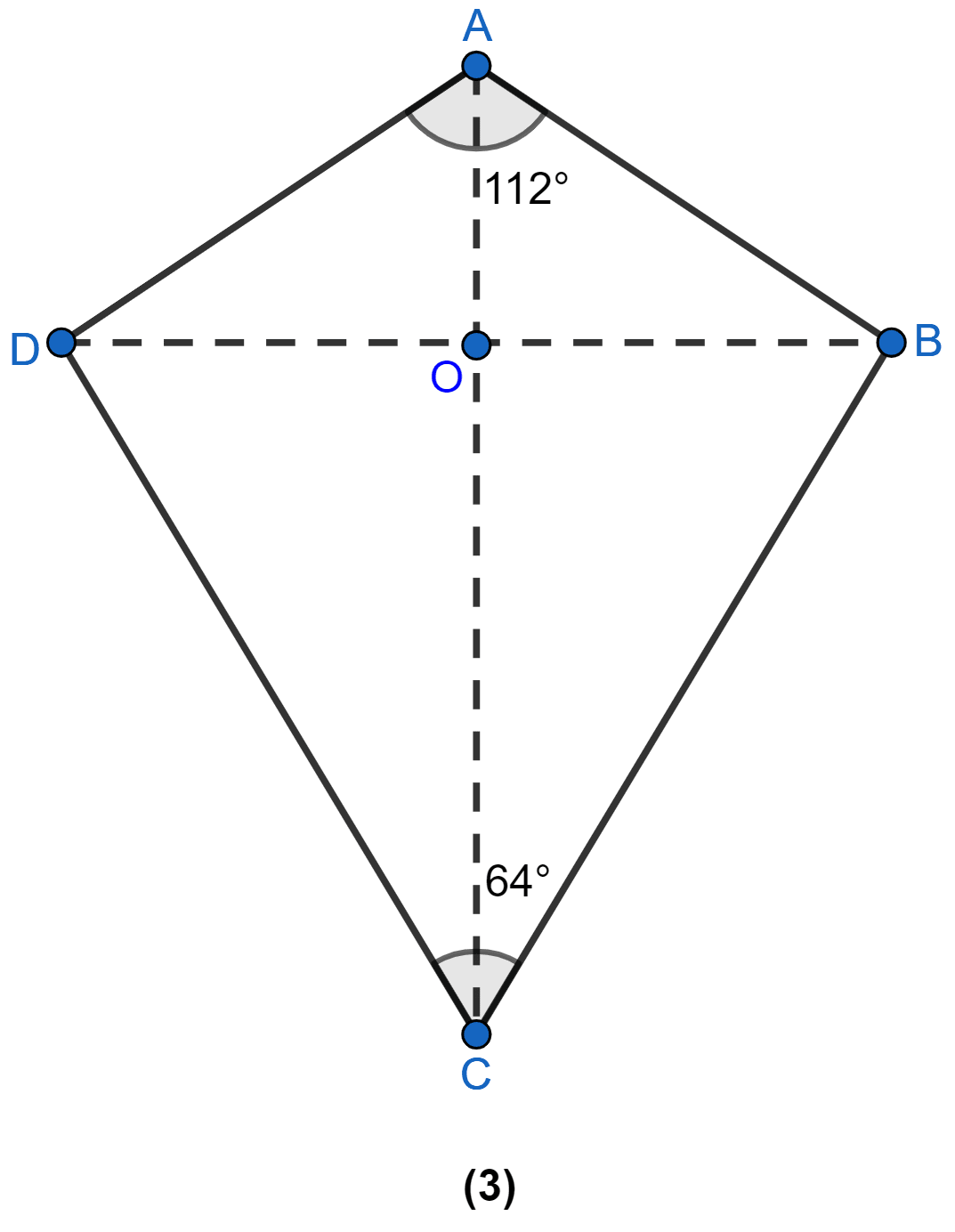
In figure (3) given below, ABCD is a kite and diagonals intersect at O. If ∠DAB = 112° and ∠DCB = 64°, find ∠ODC and ∠OBA.