Mathematics
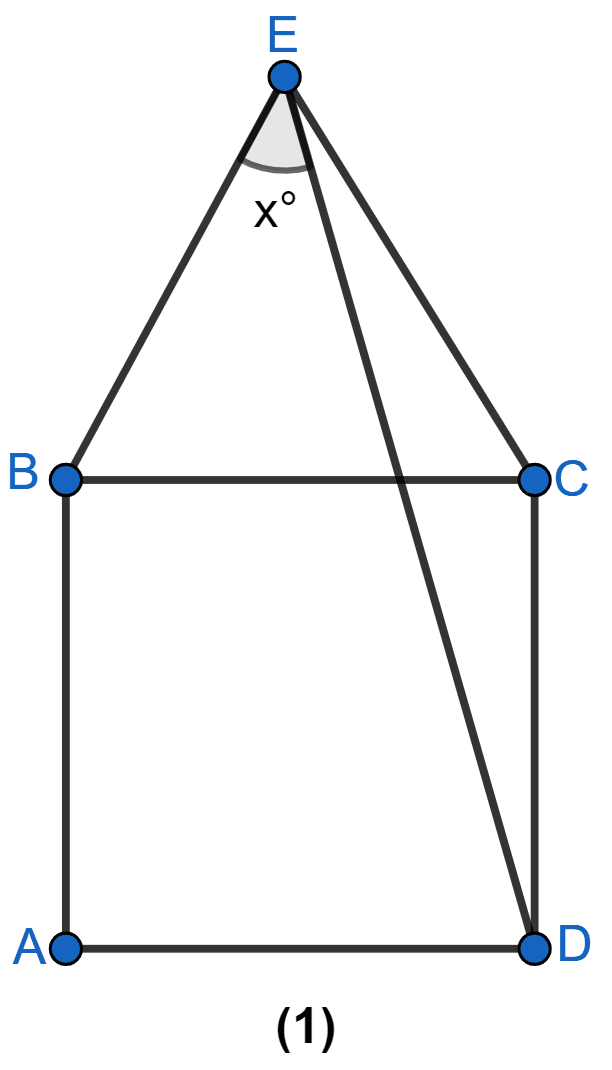
In Figure (2) given below, ABCD is a rectangle and diagonals intersect at O. AC is produced to E. If ∠ECD = 146°, find the angles of △AOB.
Rectilinear Figures
52 Likes
Answer
From figure,
∠OCD = 180° - 146° = 34° (As AE is a straight line).
The diagonals of a rectangle are equal and bisect each other.
∴ OC = OD
From figure,
In △OCD,
OC = OD
⇒ ∠ODC = ∠OCD = 34° (Angles opposite to equal sides are equal in isosceles triangle)
⇒ ∠ODC + ∠OCD + ∠DOC = 180°
⇒ 34° + 34° + ∠DOC = 180°
⇒ ∠DOC = 180° - 68° = 112°.
In △AOB,
⇒ ∠AOB = ∠DOC = 112° (Vertically opposite angles are equal).
⇒ ∠OAB = ∠OCD = 34°
⇒ ∠OBA = ∠ODC = 34°
Hence, ∠AOB = 112°, ∠OAB = 34° and ∠OBA = 34°.
Answered By
31 Likes
Related Questions
The diagonals AC and BD of a rectangle ABCD intersect each other at P. If ∠ABD = 50°, find ∠DPC.
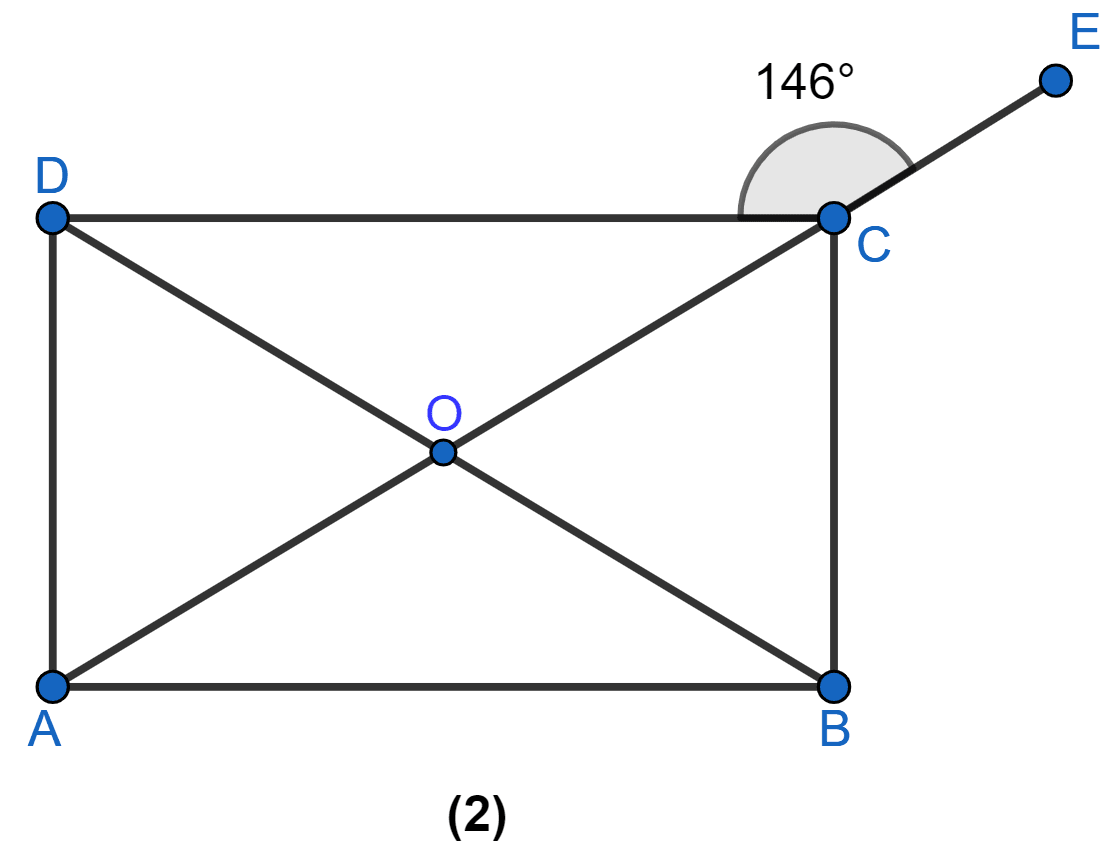
In figure (1) given below, equilateral triangle EBC surmounts square square ABCD. Find angle BED represented by x.
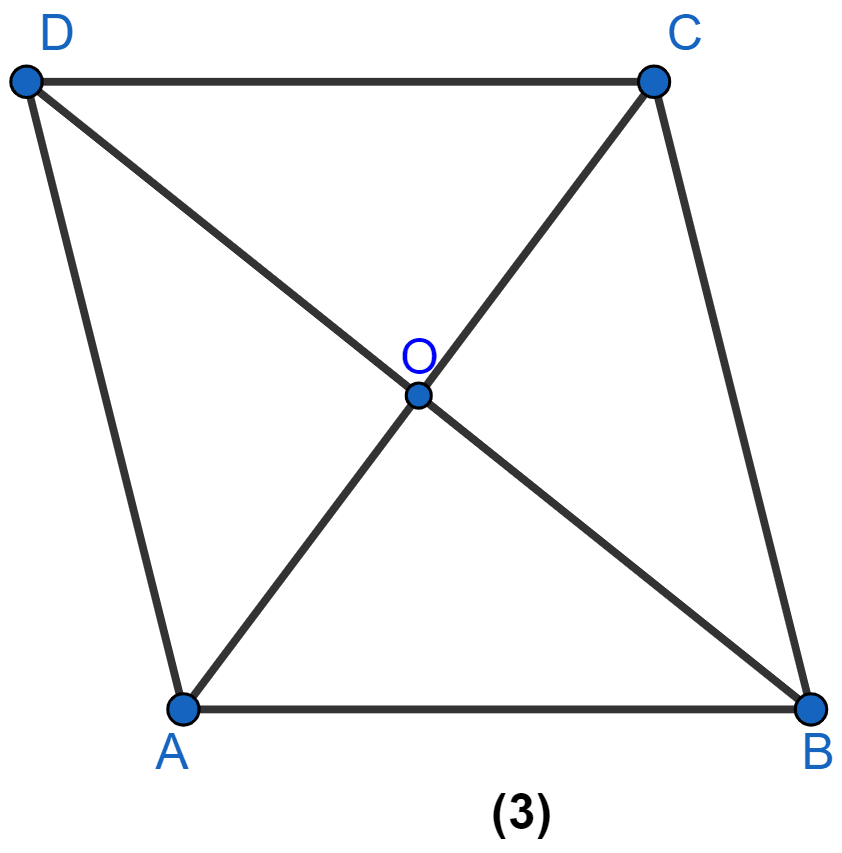
In figure (3) given below, ABCD is a rhombus and diagonals intersect at O. If ∠OAB : ∠OBA = 3 : 2, find the angles of the △AOD.
In figure (1) given below, ABCD is a trapezium. Find the values of x and y.
