Mathematics
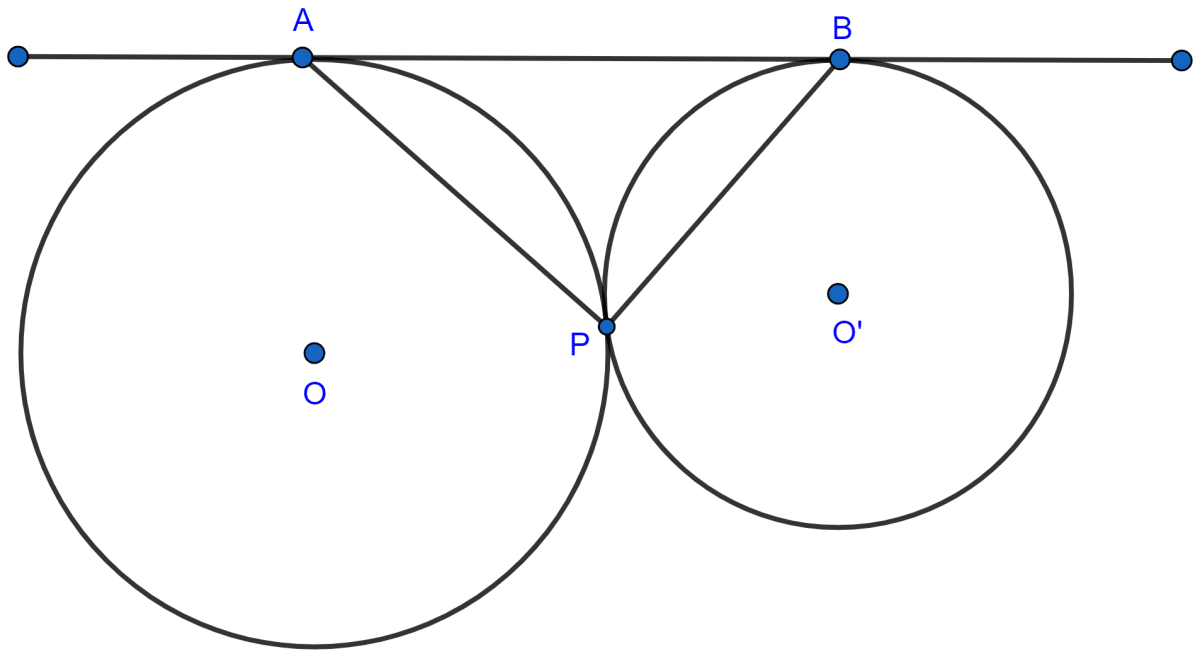
In the given figure, two circles touch each other externally at point P. AB is the direct common tangent of these circles. Prove that :
(i) tangent at point P bisects AB.
(ii) angle APB = 90°.
Answer
(i) We know that,
If two tangents are drawn to a circle from an exterior point, the tangents are equal in length.
From figure,
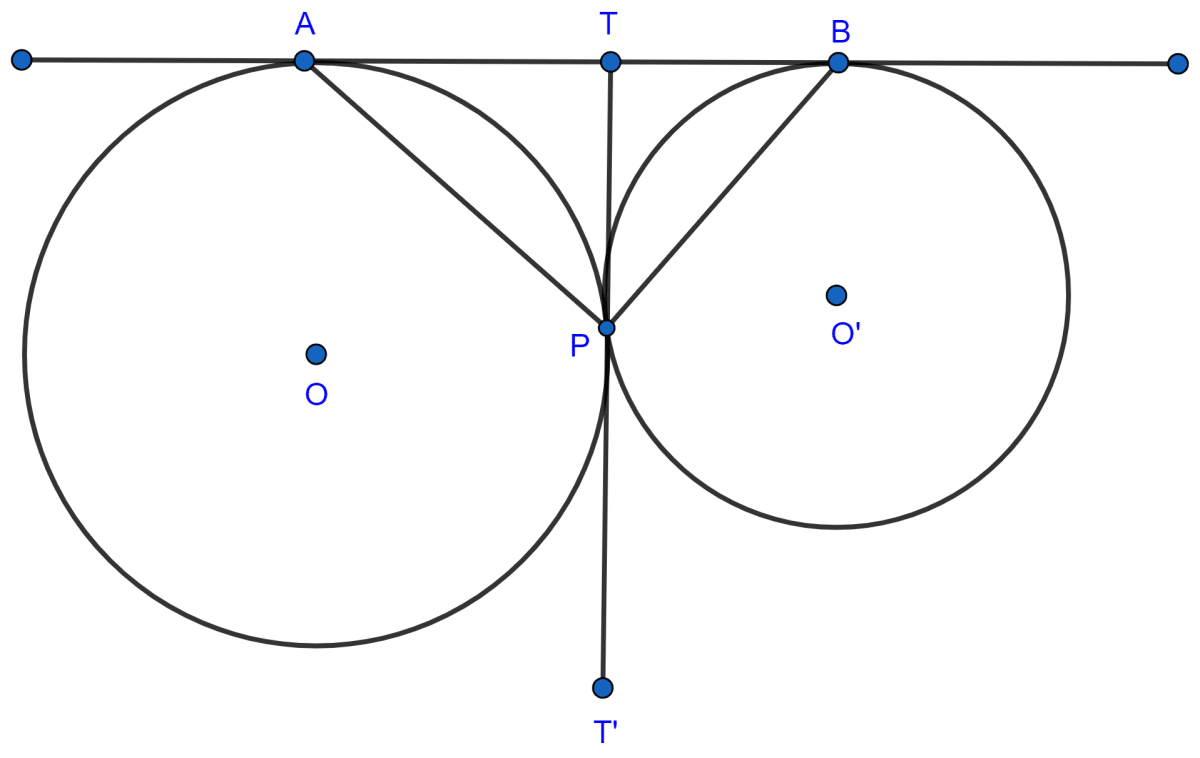
TA and TP are the tangents to the circle with center O.
∴ TA = TP ………..(1)
TB and TP are the tangents to the circle with center O'.
∴ TB = TP ………..(2)
From (1) and (2) we get :
TA = TB.
Hence, proved that tangent at point P bisects AB.
(ii) In △ATP,
TA = TP [Proved above]
∴ ∠TAP = ∠TPA ………(1) [∵ angles opposite to equal sides are equal.]
In △BTP,
TB = TP [Proved above]
∴ ∠TBP = ∠TPB ……….(2) [∵ angles opposite to equal sides are equal.]
Adding (1) and (2), we get :
∠TAP + ∠TBP = ∠TPA + ∠TPB
∠TAP + ∠TBP = ∠APB ………..(3)
In △ABP,
⇒ ∠APB + ∠BAP + ∠ABP = 180° [Angle sum property of triangle]
⇒ ∠APB + ∠TAP + ∠TBP = 180° [From figure, ∠TAP = ∠BAP and ∠TBP = ∠ABP.]
⇒ ∠APB + ∠APB = 180°
⇒ 2∠APB = 180°
⇒ ∠APB = 90°.
Hence, proved that ∠APB = 90°.
Related Questions
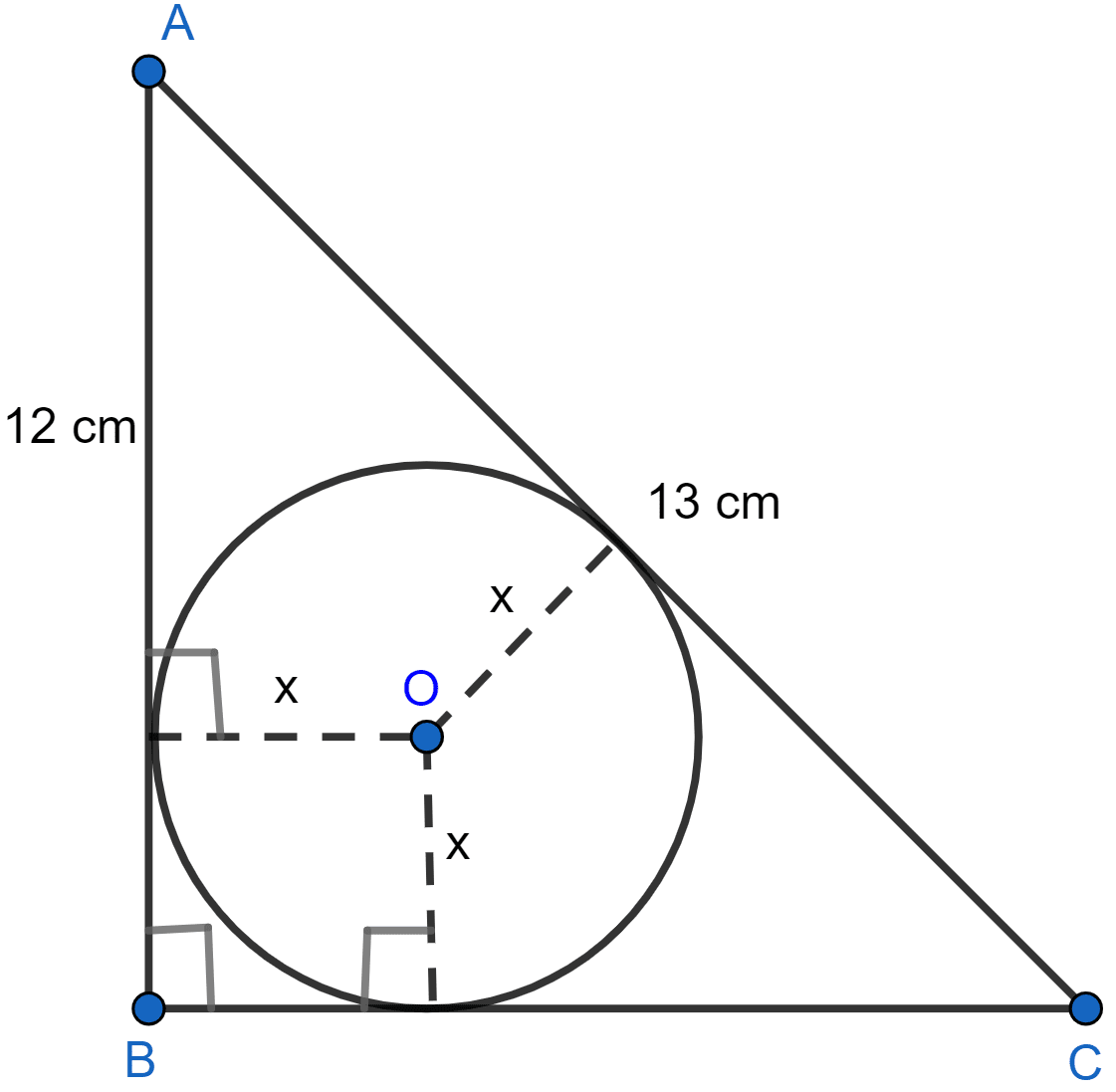
ABC is a right angled triangle with AB = 12 cm and AC = 13 cm. A circle, with center O, has been inscribed inside the triangle. Calculate the value of x, the radius of the inscribed circle.
Radii of two circles are 6.3 cm and 3.6 cm. State the distance between their centers if :
(i) they touch each other externally,
(ii) they touch each other internally.
Tangents AP and AQ are drawn to a circle, with center O, from an exterior point A. Prove that :
∠PAQ = 2∠OPQ
From a point P outside the circle, with centre O, tangents PA and PB are drawn. Prove that:
(i) ∠AOP = ∠BOP
(ii) OP is the ⊥ bisector of chord AB.