Mathematics
In the given figure, the median BD and CE of triangle ABC meet at point G. Show that BG = 2GD.
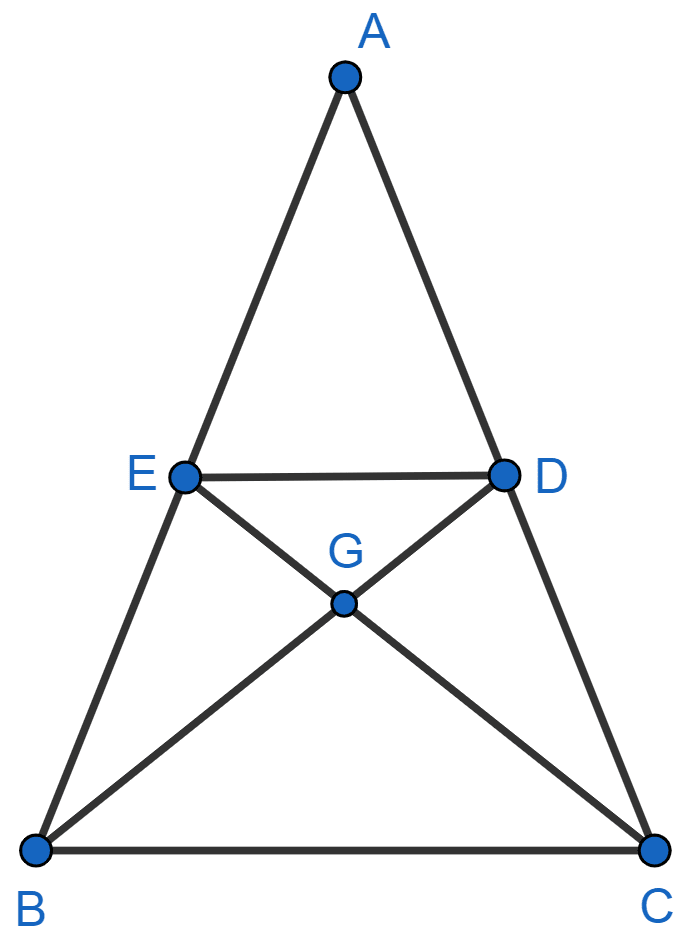
Similarity
1 Like
Answer
Since, BD and CE are medians.
∴ DA = DC and AE = BE.
∴ DE || BC (By converse of basic proportionality theorem)
In △EGD and △CGB,
⇒ ∠DEG = ∠GCB (Alternate angles are equal)
⇒ ∠EGD = ∠BGC (Vertically opposite angles are equal)
∴ △EGD ~ △CGB [By A.A. axiom]
We know that,
Ratio of corresponding sides of similar triangles are proportional.
⇒ …………..(1)
In △AED and △ABC,
⇒ ∠AED = ∠ABC (Corresponding angles are equal)
⇒ ∠EAD = ∠BAC (Common)
∴ △AED ~ △ABC [By A.A. axiom]
⇒ …………..(2)
As, E is the mid-point of AB. So,
⇒
Substituting value of in equation (2), we get :
⇒ .
Substituting value of in equation (1), we get :
⇒
⇒ GB = 2GD.
Hence, proved that GB = 2GD.
Answered By
2 Likes
Related Questions
If the mean of following distribution is . Find the missing frequency p.
C.I. f 25-35 10 35-45 6 45-55 4 55-65 p 65-75 4 75-85 12 85-95 26 Solve the inequation 3 ≥ , x ∈ I (integers). Graph the solution on a real number line.
The sides of a right-angled triangle, containing the right angle, are 3(x + 1) cm and (2x - 1) cm. If the area of the triangle is 30 cm2, find the lengths of the sides of the triangle.
The daily wages of 160 workers in a factory are given below :
Wages (in ₹) No. of workers 50-60 12 60-70 20 70-80 30 80-90 38 90-100 24 100-110 16 110-120 12 120-130 8 Draw a cumulative frequency curve and estimate :
(i) median wage
(ii) inter-quartile range
(iii) percentage of workers who earn more than ₹ 95 per day.