Mathematics
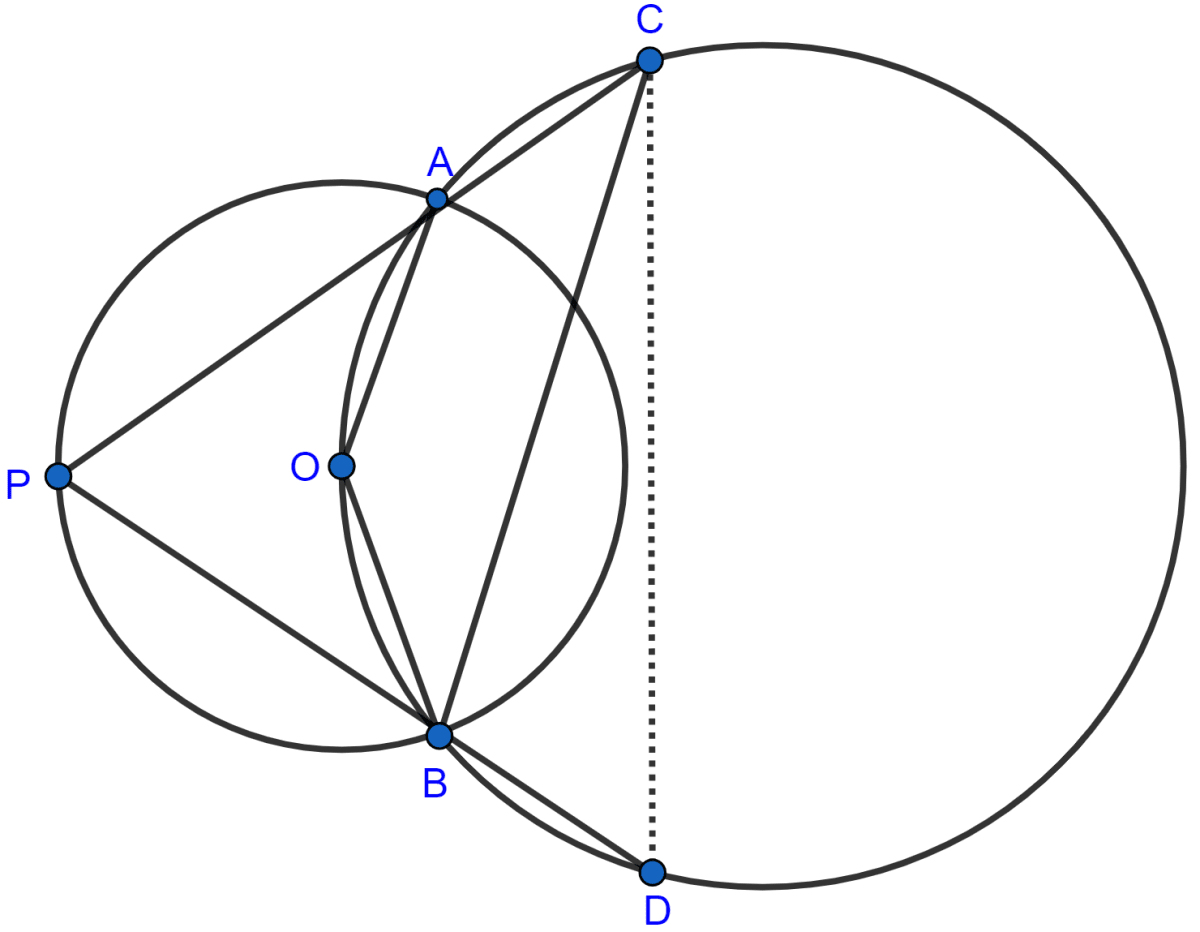
In the given figure, the center O of the small circle lies on the circumference of the bigger circle. If ∠APB = 75° and ∠BCD = 40°, find :
(i) ∠AOB,
(ii) ∠ACB,
(iii) ∠ABD,
(iv) ∠ADB.
Answer
Join AB and AD.
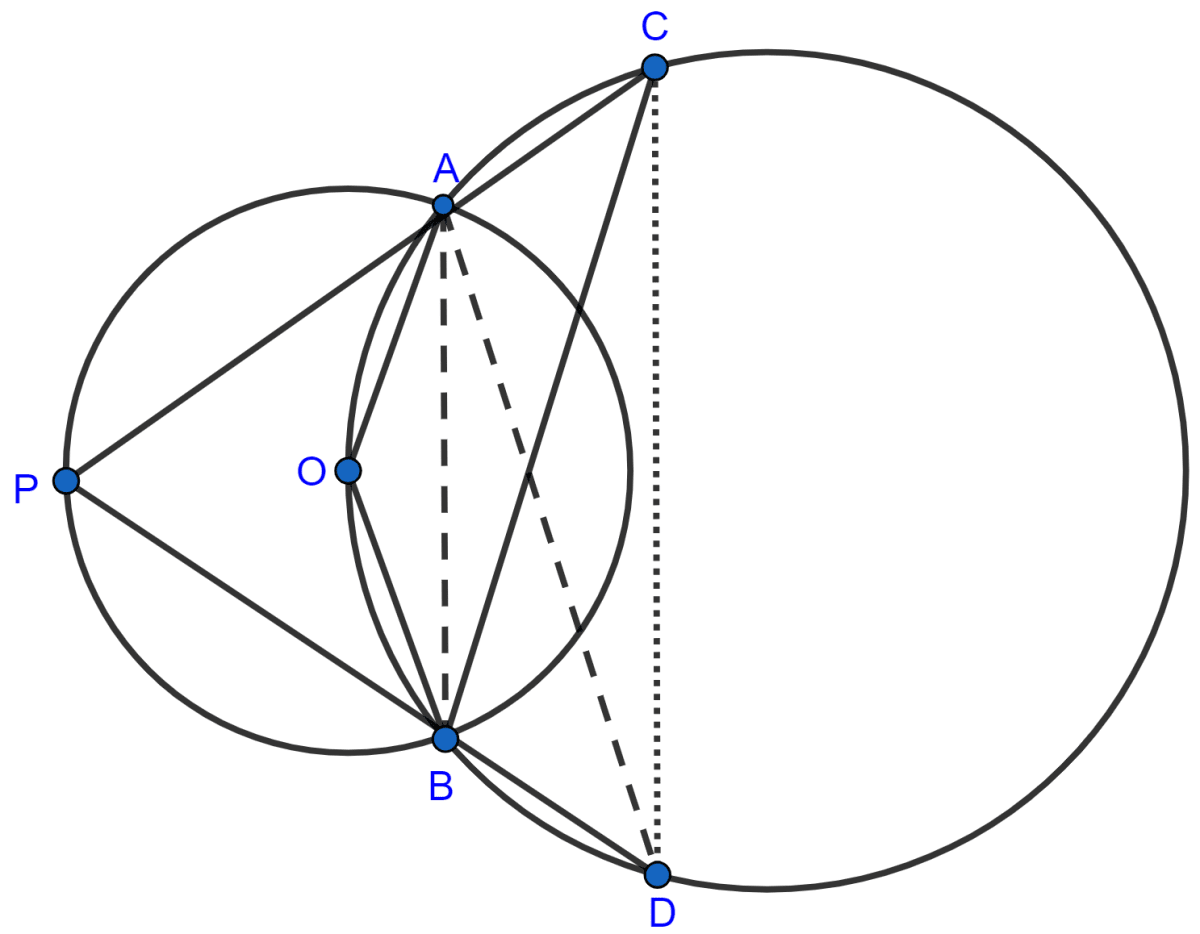
(i) We know that,
Angle which an arc subtends at the center is double that which it subtends at any point on the remaining part of the circumference.
∴ ∠AOB = 2∠APB = 2 × 75° = 150°.
Hence, ∠AOB = 150°.
(ii) We know that,
Sum of opposite angles in a cyclic quadrilateral = 180°.
∴ ∠ACB + ∠AOB = 180°
⇒ ∠ACB + 150° = 180°
⇒ ∠ACB = 180° - 150° = 30°.
Hence, ∠ACB = 30°.
(iii) From figure,
∠ACD = ∠ACB + ∠BCD = 30° + 40° = 70°.
We know that,
Sum of opposite angles in a cyclic quadrilateral = 180°.
In cyclic quadrilateral ABDC,
∴ ∠ABD + ∠ACD = 180°
⇒ ∠ABD + 70° = 180°
⇒ ∠ABD = 180° - 70° = 110°.
Hence, ∠ABD = 110°.
(iv) We know that,
Sum of opposite angles in a cyclic quadrilateral = 180°.
In cyclic quadrilateral AOBD,
∴ ∠ADB + ∠AOB = 180°
⇒ ∠ADB + 150° = 180°
⇒ ∠ADB = 180° - 150° = 30°.
Hence, ∠ADB = 30°.
Related Questions
In the given figure, ∠BAD = 65°, ∠ABD = 70° and ∠BDC = 45°. Find :
(i) ∠BCD
(ii) ∠ACB
Hence, show that AC is a diameter.

AB is the diameter of the circle with center O. OD is parallel to BC and ∠AOD = 60°. Calculate the numerical values of :
(i) ∠ABD,
(ii) ∠DBC,
(iii) ∠ADC.
In a cyclic quadrilateral ABCD, ∠A : ∠C = 3 : 1 and ∠B : ∠D = 1 : 5; find each angle of the quadrilateral.
In the given figure, PQ is a diameter. Chord SR is parallel to PQ. Given that ∠PQR = 58°, Calculate :
(i) ∠RPQ
(ii) ∠STP.
