Mathematics
In a cyclic quadrilateral ABCD, ∠A : ∠C = 3 : 1 and ∠B : ∠D = 1 : 5; find each angle of the quadrilateral.
Circles
9 Likes
Answer
Let ∠A = 3x and ∠C = x.
In cyclic quadrilateral ABCD,
⇒ ∠A + ∠C = 180° [Sum of opposite angles in a cyclic quadrilateral = 180°]
⇒ 3x + x = 180°
⇒ 4x = 180°
⇒ x = = 45°.
∠A = 3x = 3 x 45 = 135°
∠C = x = 45°.
Let ∠B = y and ∠D = 5y.
In cyclic quadrilateral ABCD,
⇒ ∠B + ∠D = 180° [Sum of opposite angles in a cyclic quadrilateral = 180°]
⇒ y + 5y = 180°
⇒ 6y = 180°
⇒ y = = 30°.
∠B = y = 30°
∠D = 5y = 5 x 30° = 150°.
Hence, ∠A = 135°, ∠B = 30°, ∠C = 45° and ∠D = 150°.
Answered By
5 Likes
Related Questions
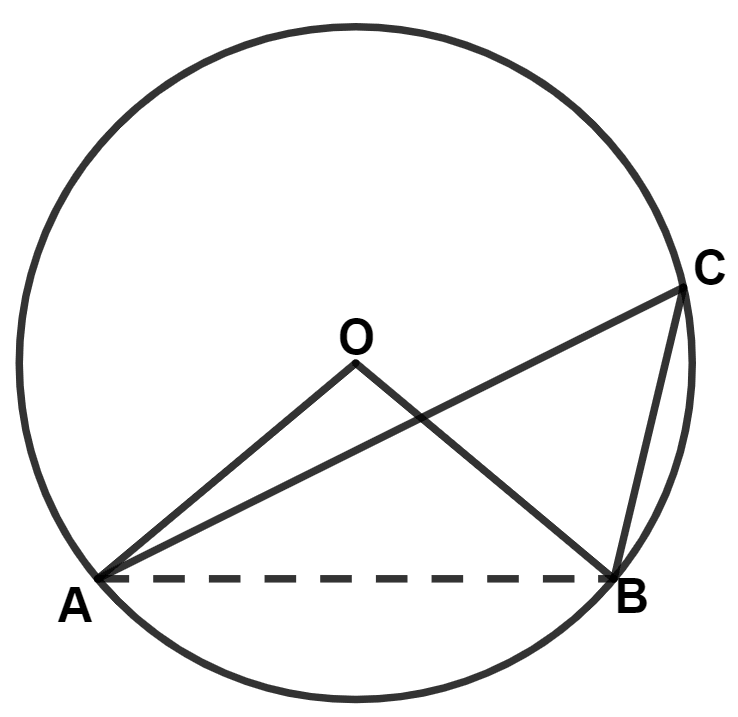
In the given figure, the center O of the small circle lies on the circumference of the bigger circle. If ∠APB = 75° and ∠BCD = 40°, find :
(i) ∠AOB,
(ii) ∠ACB,
(iii) ∠ABD,
(iv) ∠ADB.
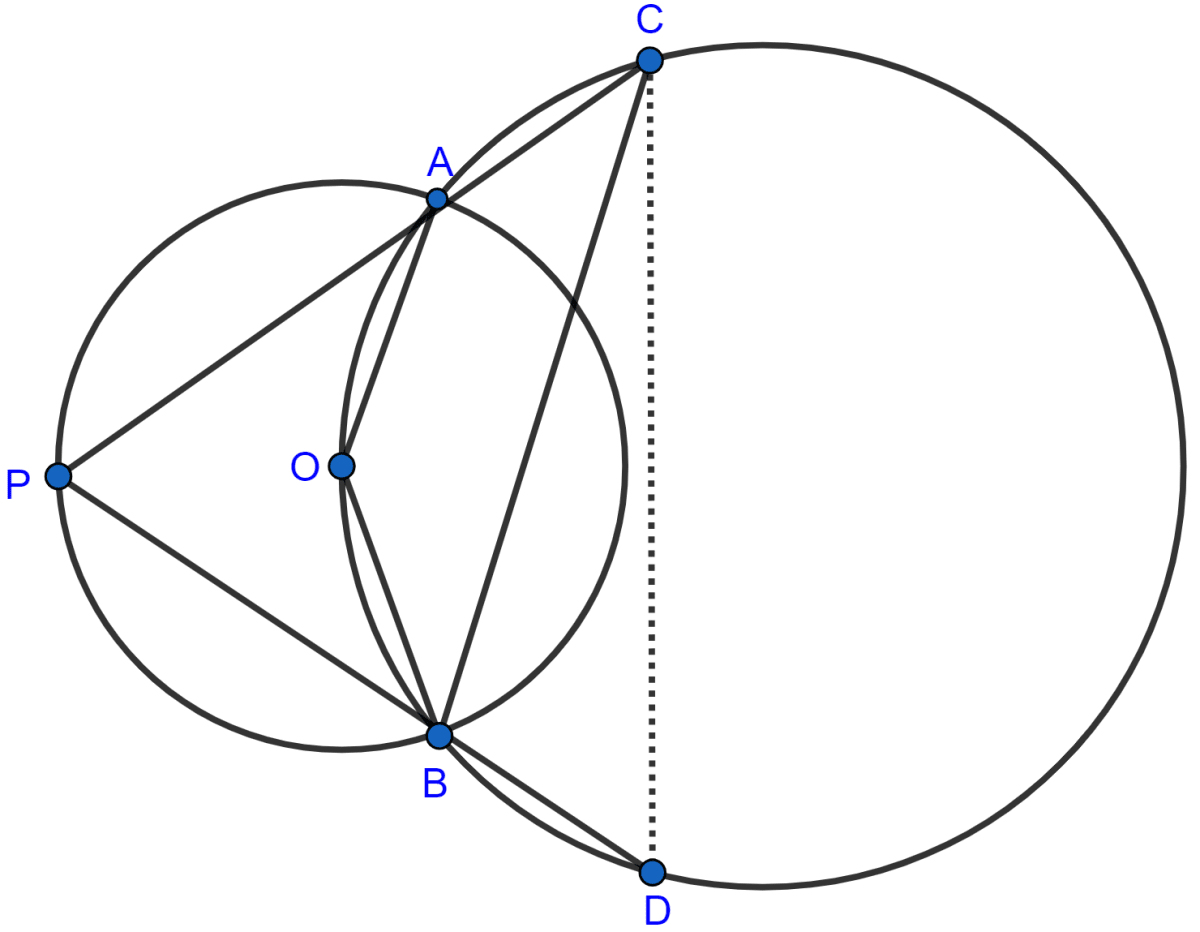
In the given figure, ∠BAD = 65°, ∠ABD = 70° and ∠BDC = 45°. Find :
(i) ∠BCD
(ii) ∠ACB
Hence, show that AC is a diameter.

In the given figure, O is the center of the circle and chord AB : chord CD = 3 : 5. If angle AOB = 60°, angle COD is equal to :
60°
120°
90°
100°
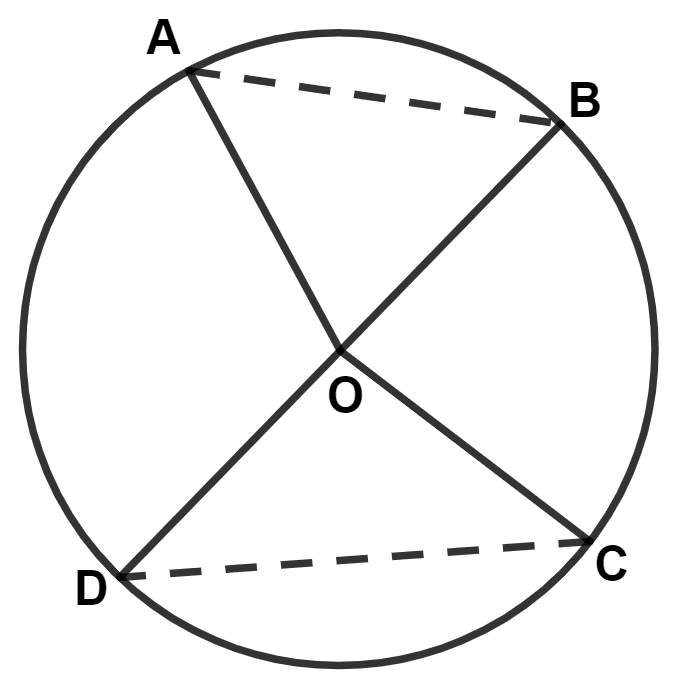
In the given figure, O is the center of the circle and angle OAB = 55°, then angle ACB is equal to :
55°
35°
70°
30°