Mathematics
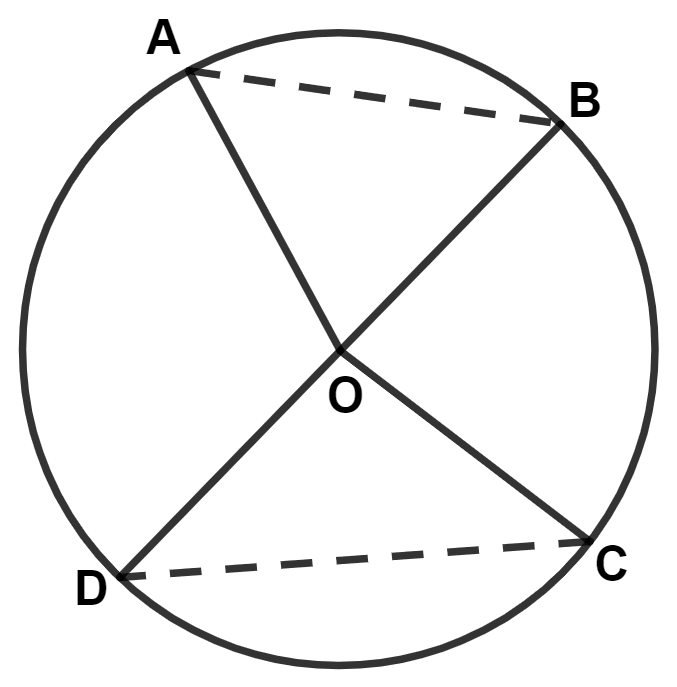
In the given figure, ∠BAD = 65°, ∠ABD = 70° and ∠BDC = 45°. Find :
(i) ∠BCD
(ii) ∠ACB
Hence, show that AC is a diameter.

Circles
28 Likes
Answer
(i) We know that,
Sum of opposite angles in a cyclic quadrilateral = 180°.
In cyclic quadrilateral ABCD,
∴ ∠BCD + ∠BAD = 180°
⇒ ∠BCD + 65° = 180°
⇒ ∠BCD = 180° - 65° = 115°.
Hence, ∠BCD = 115°.
(ii) In △ABD,
⇒ ∠ADB + ∠BAD + ∠DBA = 180° [Angle sum property of triangle]
⇒ ∠ADB + 65° + 70° = 180°
⇒ ∠ADB + 135° = 180°
⇒ ∠ADB = 180° - 135° = 45°.
We know that,
Angles in same segment are equal.
∴ ∠ACB = ∠ADB = 45°.
Hence, ∠ADB = 45°.
From figure,
∠ADC = ∠ADB + ∠BDC = 45° + 45° = 90°.
Since, angle in a semi-circle is a right angle.
Hence, proved that AC is a diameter.
Answered By
14 Likes
Related Questions
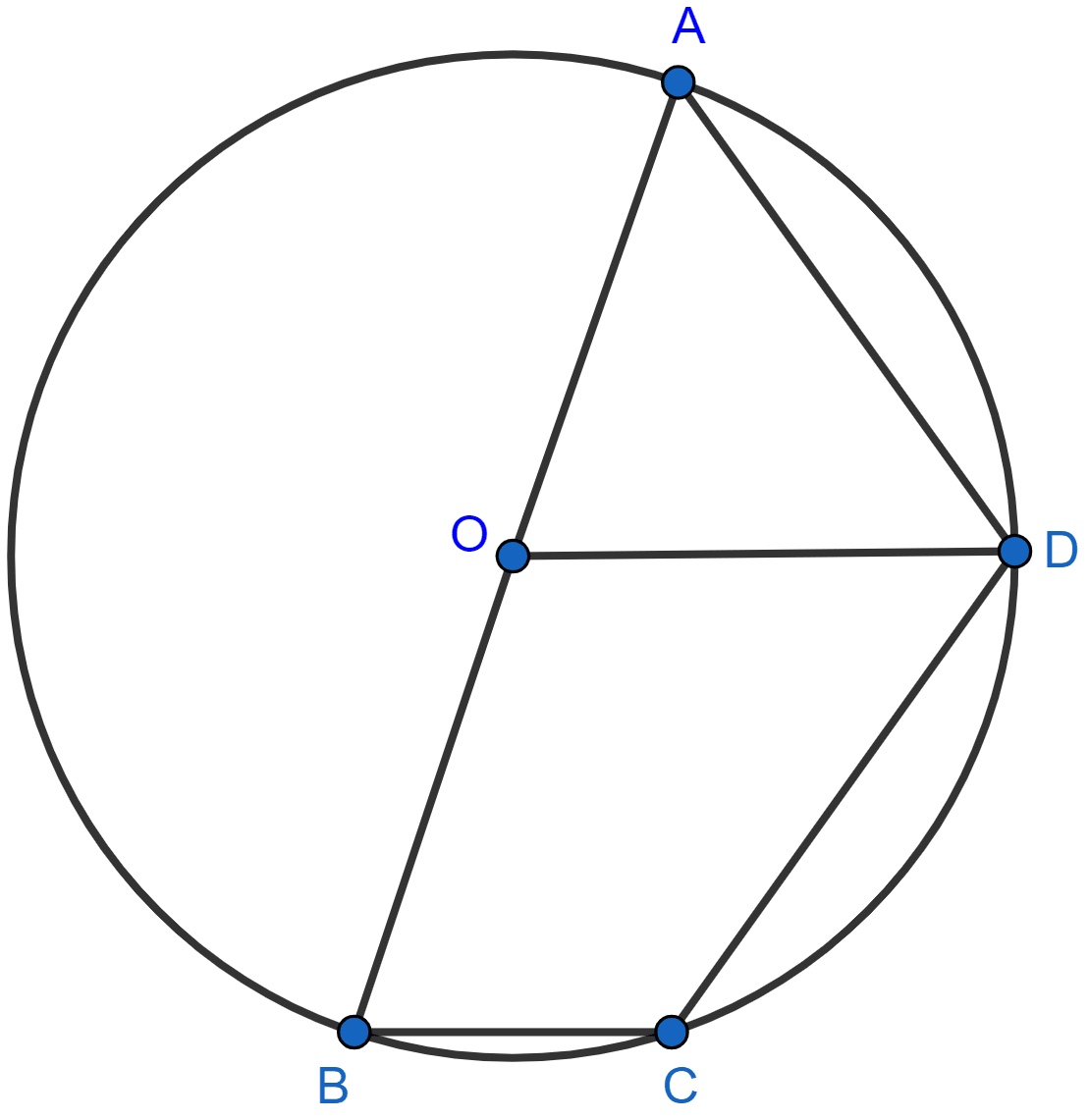
AB is the diameter of the circle with center O. OD is parallel to BC and ∠AOD = 60°. Calculate the numerical values of :
(i) ∠ABD,
(ii) ∠DBC,
(iii) ∠ADC.
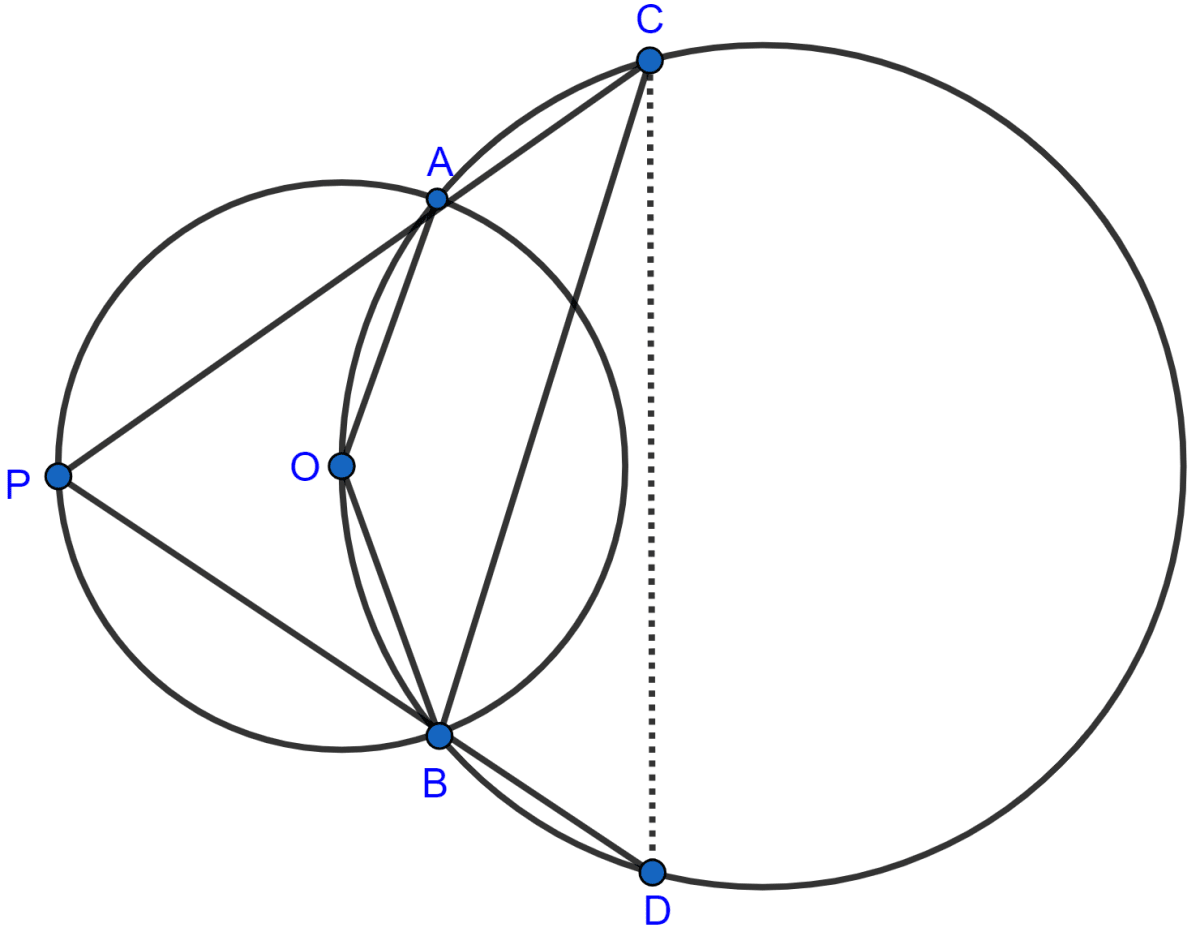
In the given figure, the center O of the small circle lies on the circumference of the bigger circle. If ∠APB = 75° and ∠BCD = 40°, find :
(i) ∠AOB,
(ii) ∠ACB,
(iii) ∠ABD,
(iv) ∠ADB.
In a cyclic quadrilateral ABCD, ∠A : ∠C = 3 : 1 and ∠B : ∠D = 1 : 5; find each angle of the quadrilateral.
In the given figure, O is the center of the circle and chord AB : chord CD = 3 : 5. If angle AOB = 60°, angle COD is equal to :
60°
120°
90°
100°