Mathematics
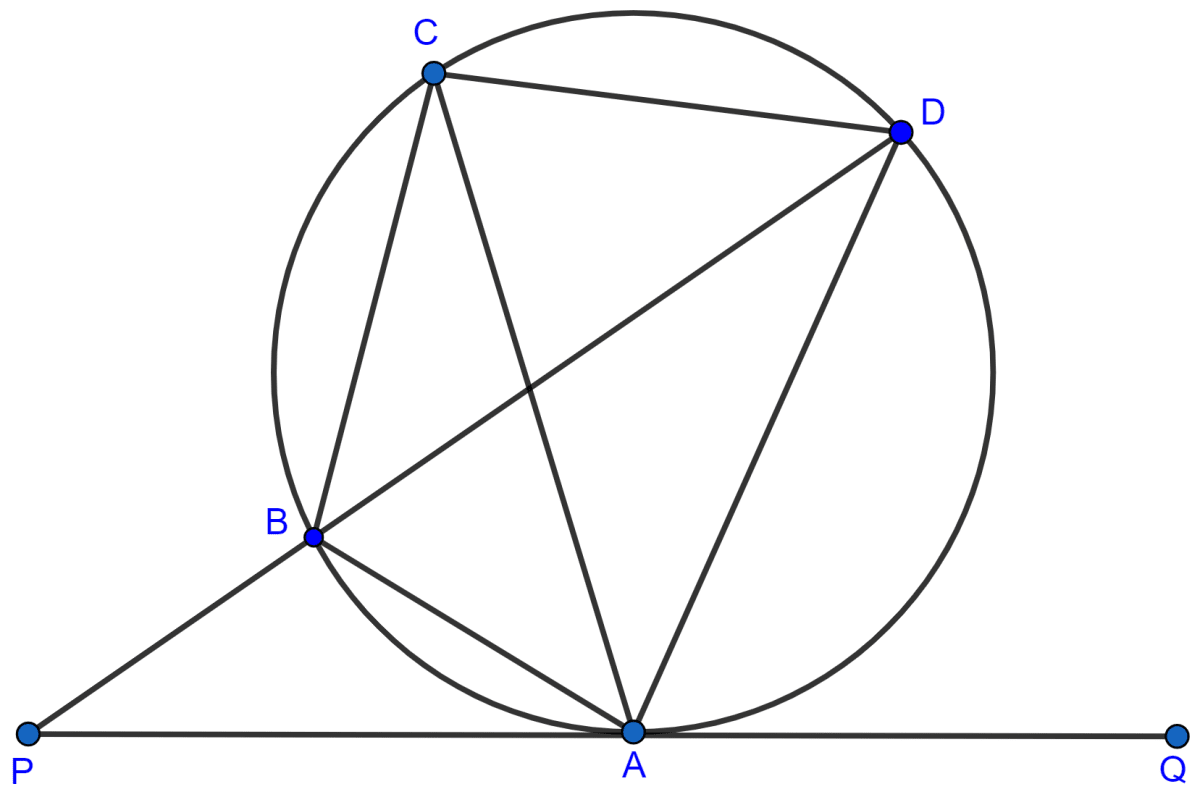
In the given figure, QAP is the tangent at point A and PBD is a straight line.
If ∠ACB = 36° and ∠APB = 42°, find :
(i) ∠BAP
(ii) ∠ABD
(iii) ∠QAD
(iv) ∠BCD
Answer
(i) We know that,
The angle between a tangent and a chord through the point of contact is equal to an angle in the alternate segment.
∴ ∠BAP = ∠ACB = 36°.
Hence, ∠BAP = 36°.
(ii) We know that,
An exterior angle in a triangle is equal to the sum of two opposite interior angles.
In △APB,
∠ABD = ∠APB + ∠BAP = 42° + 36° = 78°.
Hence, ∠ABD = 78°.
(iii) From figure,
∠ADB = ∠ACB = 36° (Angles in same segment are equal)
In △PAD,
∠QAD = ∠APB + ∠ADB = 42° + 36° = 78°. [Exterior angle is equal to sum of two opposite interior angles.]
Hence, ∠QAD = 78°.
(iv) We know that,
The angle between a tangent and a chord through the point of contact is equal to an angle in the alternate segment.
∴ ∠ACD = ∠QAD = 78°.
From figure,
∠BCD = ∠ACB + ∠ACD = 36° + 78° = 114°.
Hence, ∠BCD = 114°.
Related Questions
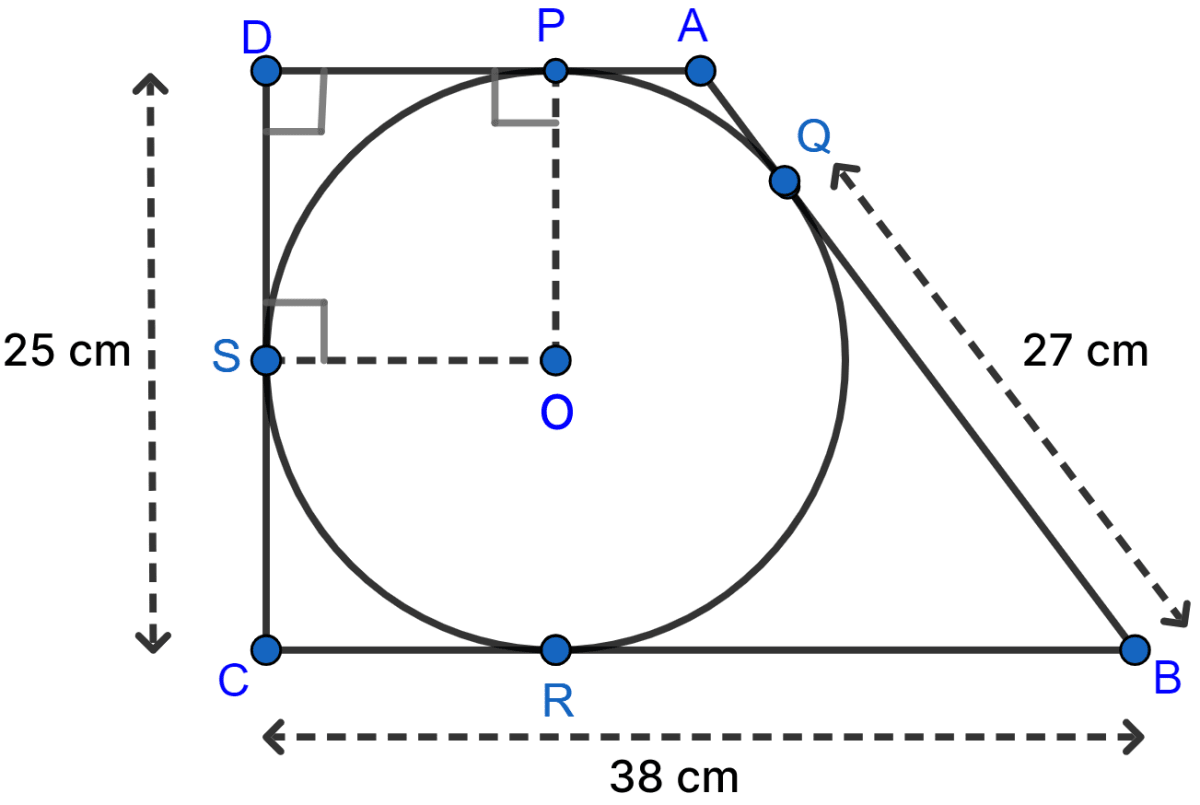
In the following figure, a circle is inscribed in the quadrilateral ABCD. If BC = 38 cm, QB = 27 cm, DC = 25 cm and that AD is perpendicular to DC, find the radius of the circle.
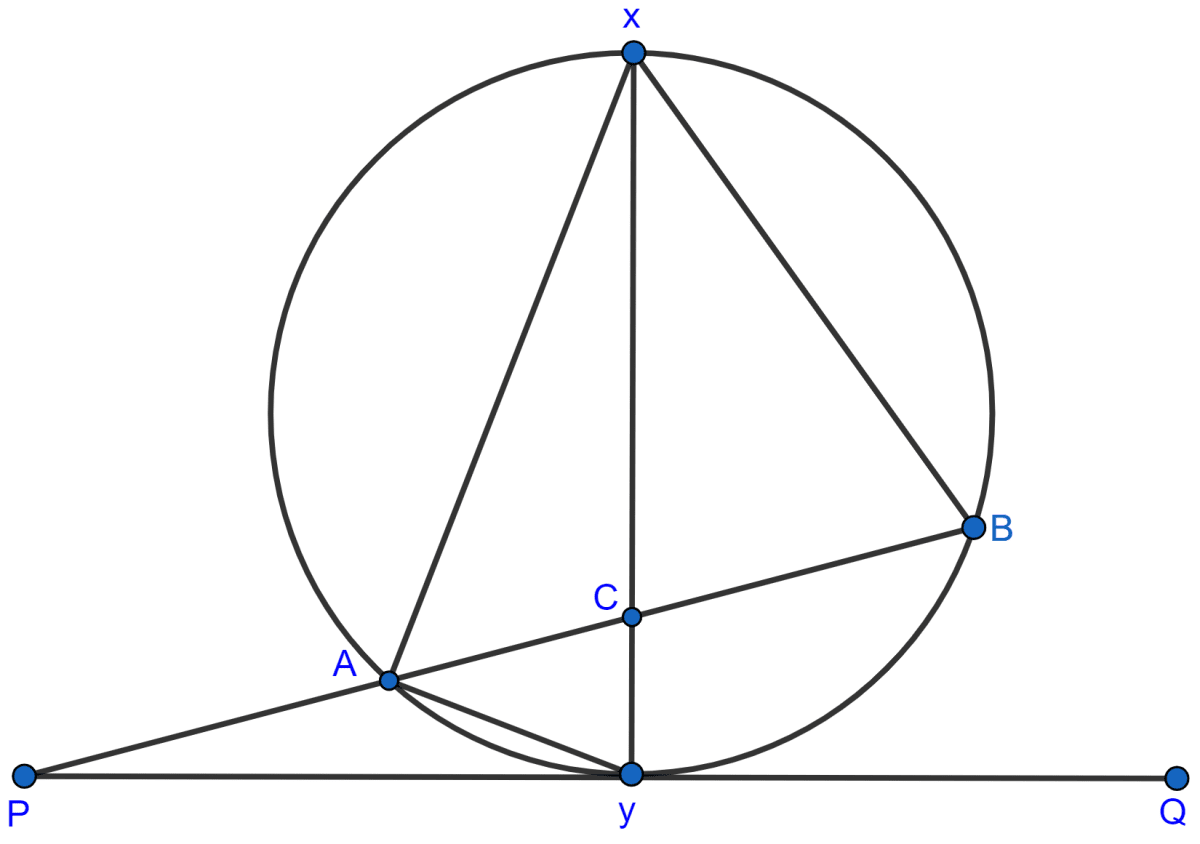
In the given figure, XY is the diameter of the circle and PQ is a tangent to the circle at Y.
If ∠AXB = 50° and ∠ABX = 70°, find ∠BAY and ∠APY.
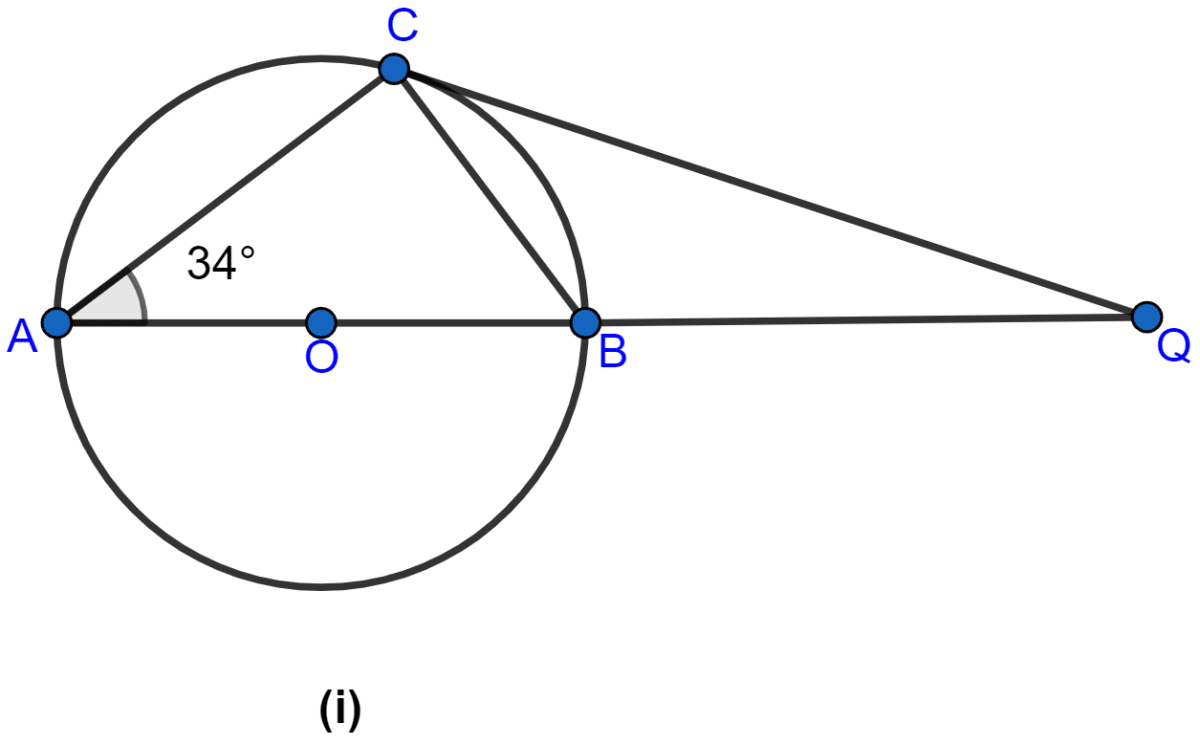
In the figure (i) given below, AB is a diameter. The tangent at C meets AB produced at Q, ∠CAB = 34°. Find :
(i) ∠CBA
(ii) ∠CQA
In the given figure, O is the center of the circle. The tangents at B and D intersect each other at point P. If AB is parallel to CD and ∠ABC = 55°, find :
(i) ∠BOD
(ii) ∠BPD
