Mathematics
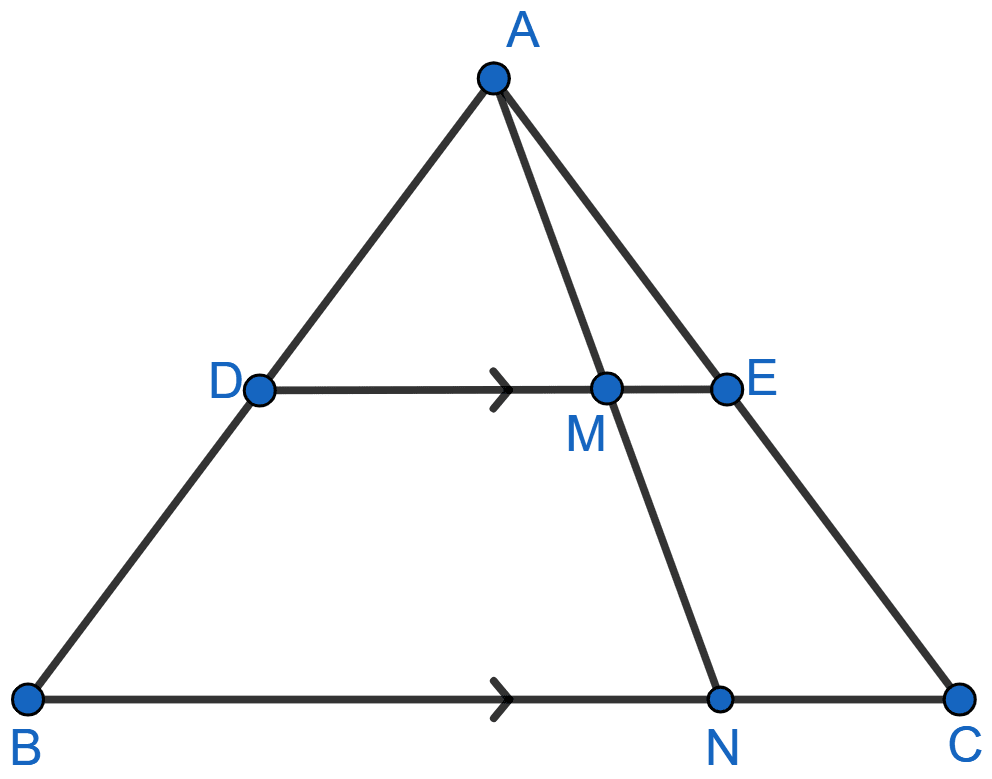
In the given figure, DE || BC, AE = 15 cm, EC = 9 cm, NC = 6 cm and BN = 24 cm.
(i) Write all possible pairs of similar triangles.
(ii) Find the lengths of ME and DM.
Similarity
Answer
(i) In ΔAME and ΔANC,
⇒ ∠AME = ∠ANC [Since DE || BC so, ME || NC and AN is transversal]
⇒ ∠MAE = ∠NAC [Common angle]
∴ ∆AME ~ ∆ANC [By AA]
In ΔADM and ΔABN,
⇒ ∠ADM = ∠ABN [Since DE || BC so, DM || BN and AB is transversal]
⇒ ∠DAM = ∠BAN [Common angle]
∴ ∆ADM ~ ∆ABN [By AA]
In ΔADE and ΔABC,
⇒ ∠ADE = ∠ABC [Since DE || BC and AB is transversal]
⇒ ∠AED = ∠ACB [Since DE || BC and AC is transversal]
∴ ∆ADE ~ ∆ABC [By AA]
Hence, ∆ADM ~ ∆ABN, ∆AME ~ ∆ANC and ∆ADE ~ ∆ABC.
(ii) Since, ∆AME ~ ∆ANC
We know that,
Corresponding sides of similar triangles are proportional.
Since, ∆ADE ~ ∆ABC [Proved above]
We know that,
Corresponding sides of similar triangles are proportional.
……… (1)
Also, ∆ADM ~ ∆ABN [Proved above]
Hence, ME = 3.75 cm and DM = 15 cm.
Answered By
Related Questions
In ΔABC, angle ABC is equal to twice the angle ACB, and bisector of angle ABC meets the opposite side at point P. Show that :
(i) CB : BA = CP : PA
(ii) AB x BC = BP x CA
In ΔABC, BM ⊥ AC and CN ⊥ AB; show that:
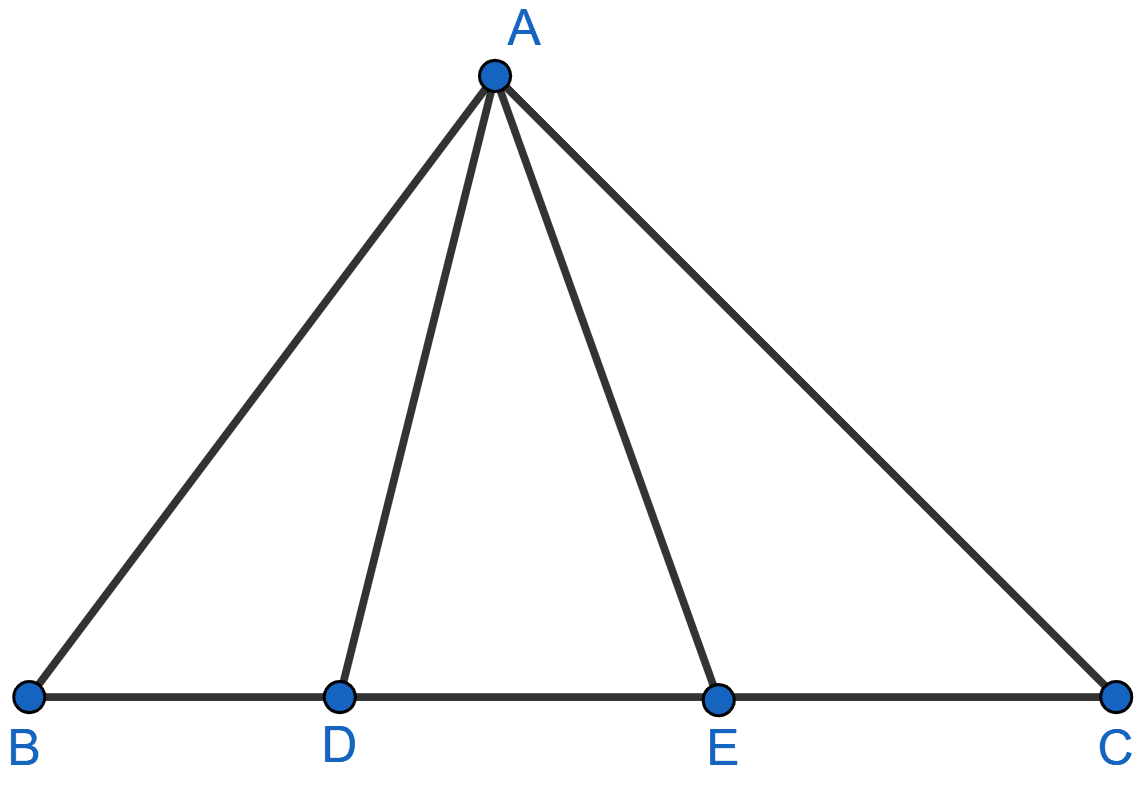
In the given figure, AD = AE and AD2 = BD x EC. Prove that: triangles ABD and CAE are similar.
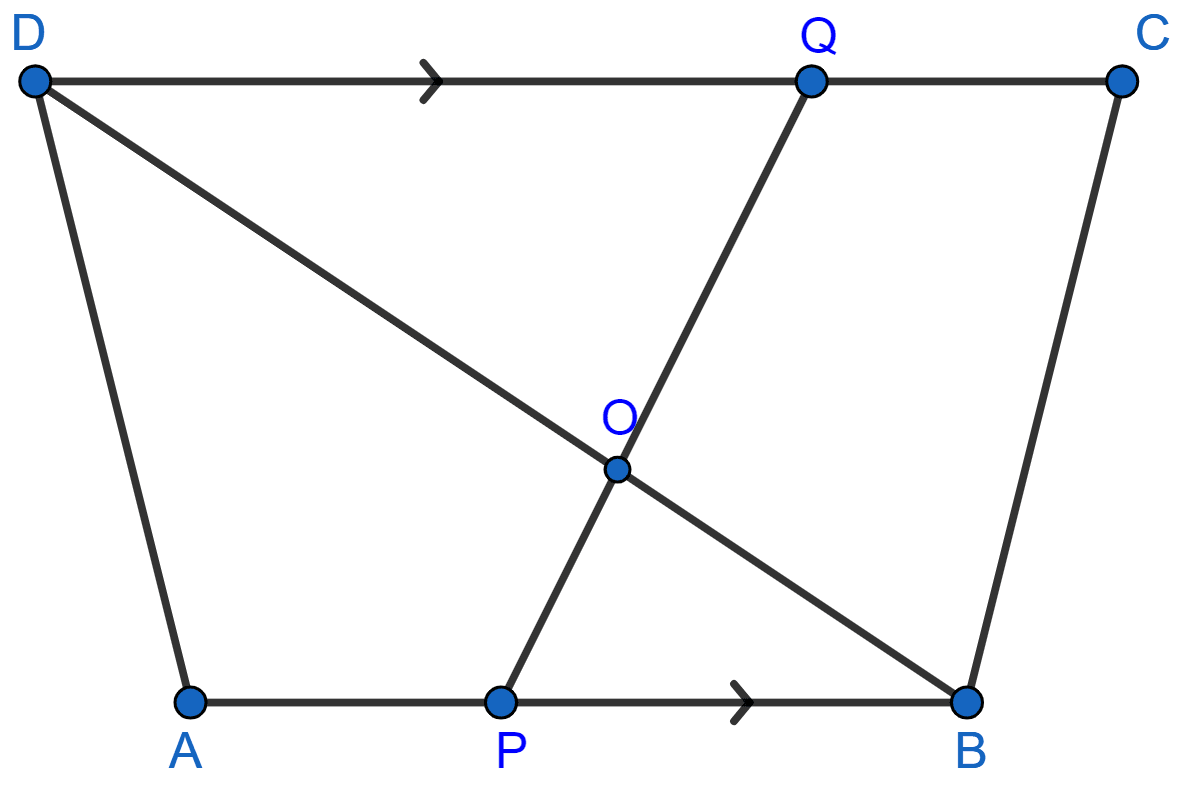
In the given figure, AB || DC, BO = 6 cm and DQ = 8 cm; find: BP x DO.