Mathematics
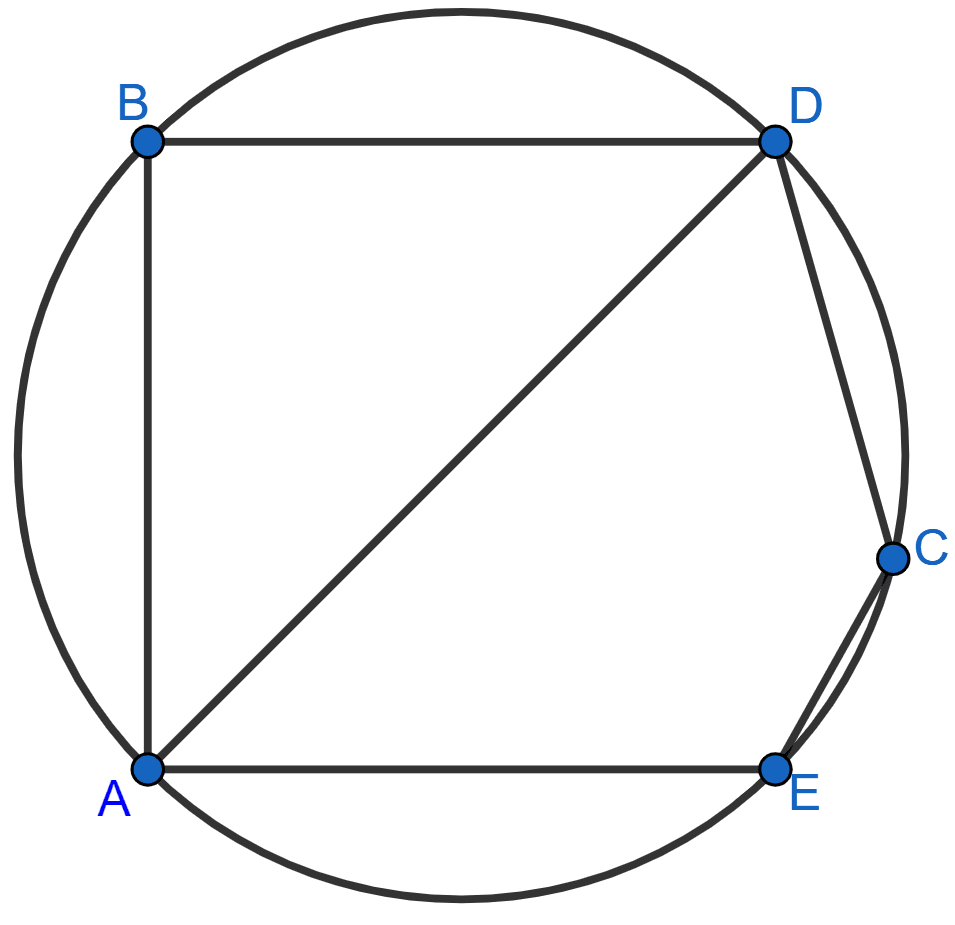
In the given figure, BD is a side of regular hexagon, DC is a side of a regular pentagon and AD is a diameter. Calculate :
(i) ∠ADC,
(ii) ∠BDA,
(iii) ∠ABC,
(iv) ∠AEC.
Circles
7 Likes
Answer
Let O be the center of the circle.
Join BC, BO, CO and EO.
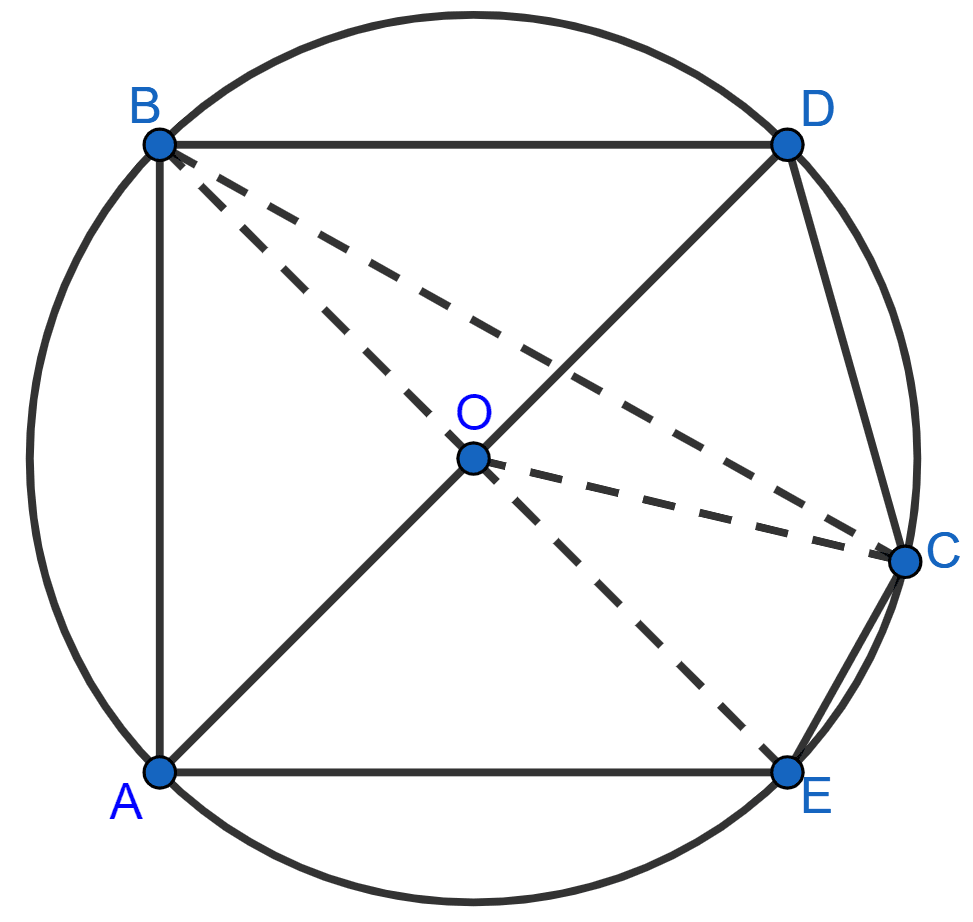
Since, BD is the side of a regular hexagon,
∴ ∠BOD = = 60°.
Since, DC is the side of a regular pentagon,
∴ ∠COD = = 72°.
In △BOD,
OB = OD [Radii of same circle]
∴ ∠OBD = ∠ODB = x (let) [Angles opposite to equal sides are equal]
⇒ ∠OBD + ∠ODB + ∠BOD = 180°
⇒ x + x + 60° = 180°
⇒ 2x = 180° - 60°
⇒ 2x = 120°
⇒ x = = 60°.
(i) In △OCD,
⇒ OD = OC [Radii of same circle]
⇒ ∠ODC = ∠OCD = y (let) [Angles opposite to equal sides are equal]
⇒ ∠OCD + ∠ODC + ∠COD = 180°
⇒ y + y + 72° = 180°
⇒ 2y = 180° - 72°
⇒ 2y = 108°
⇒ y = = 54°.
From figure,
∠ADC = ∠ODC = y = 54°.
Hence, ∠ADC = 54°.
(ii) From figure,
∠BDA = ∠BDO = 60°.
Hence, ∠BDA = 60°.
(iii) We know that,
Angle at the centre is twice the angle at remaining circumference.
Arc AC subtends ∠AOC at the centre and ∠ABC at the remaining part of the circle.
∴ ∠AOC = 2∠ABC
⇒ ∠ABC = ∠AOC
⇒ ∠ABC = [∠AOD - ∠COD]
⇒ ∠ABC = [180° - 72°]
⇒ ∠ABC =
⇒ ∠ABC = 54°.
Hence, ∠ABC = 54°.
(iv) In cyclic quadrilateral AECD,
⇒ ∠AEC + ∠ADC = 180°
⇒ ∠AEC + 54° = 180°
⇒ ∠AEC = 180° - 54°
⇒ ∠AEC = 126°.
Hence, ∠AEC = 126°.
Answered By
6 Likes
Related Questions
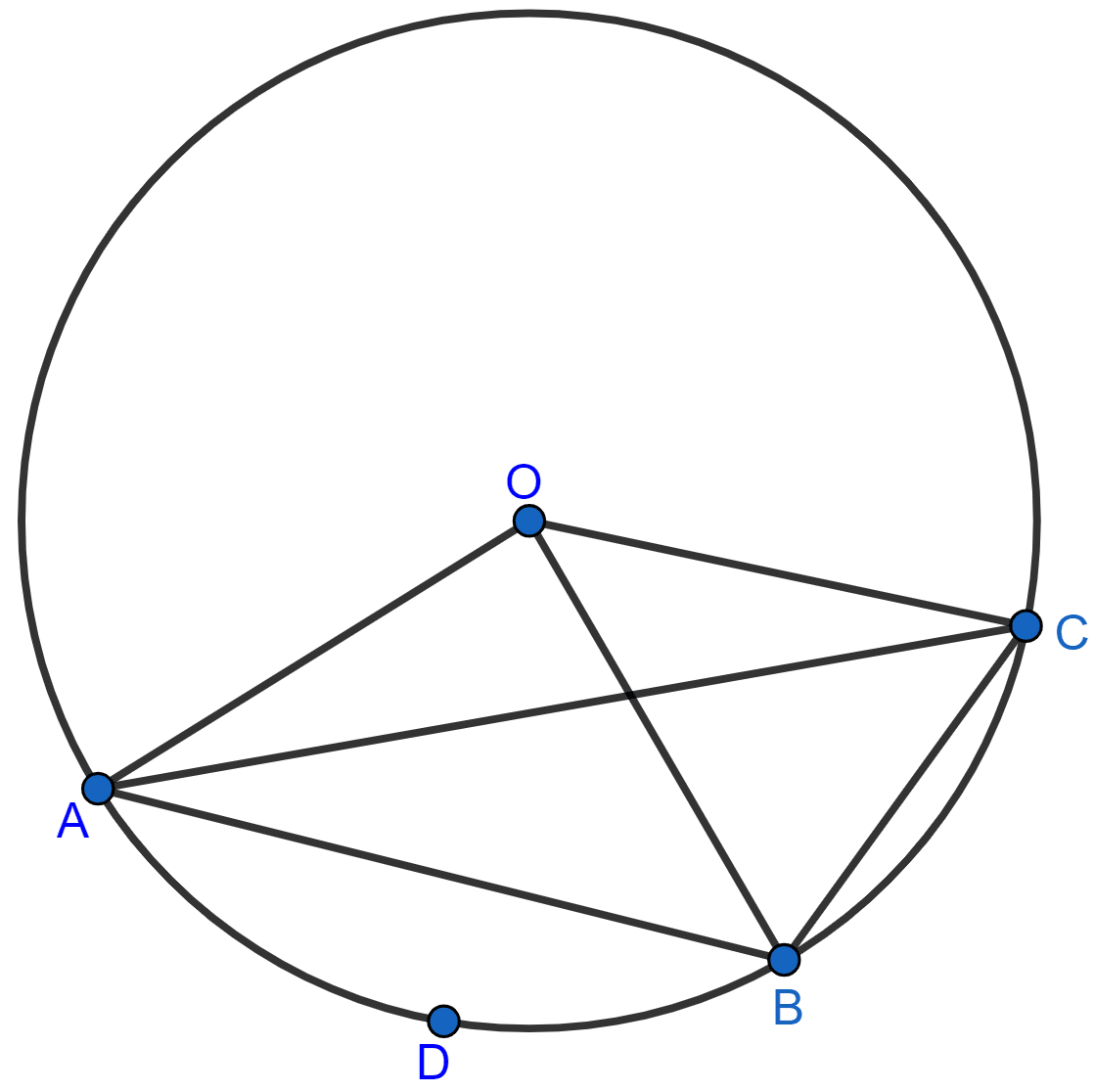
In the figure, O is the centre of the circle and the length of arc AB is twice the length of arc BC. If angle AOB = 108°, find :
(i) ∠CAB,
(ii) ∠ADB.
In the given figure, AB = BC = CD and ∠ABC = 132°. Calculate :
(i) ∠AEB,
(ii) ∠AED,
(iii) ∠COD.

In a regular pentagon ABCDE, inscribed in a circle; find the ratio between angle EDA and angle ADC.
The figure shows a circle with centre O. AB is the side of regular pentagon and AC is the side of regular hexagon.
Find the angles of triangle ABC.
