Mathematics
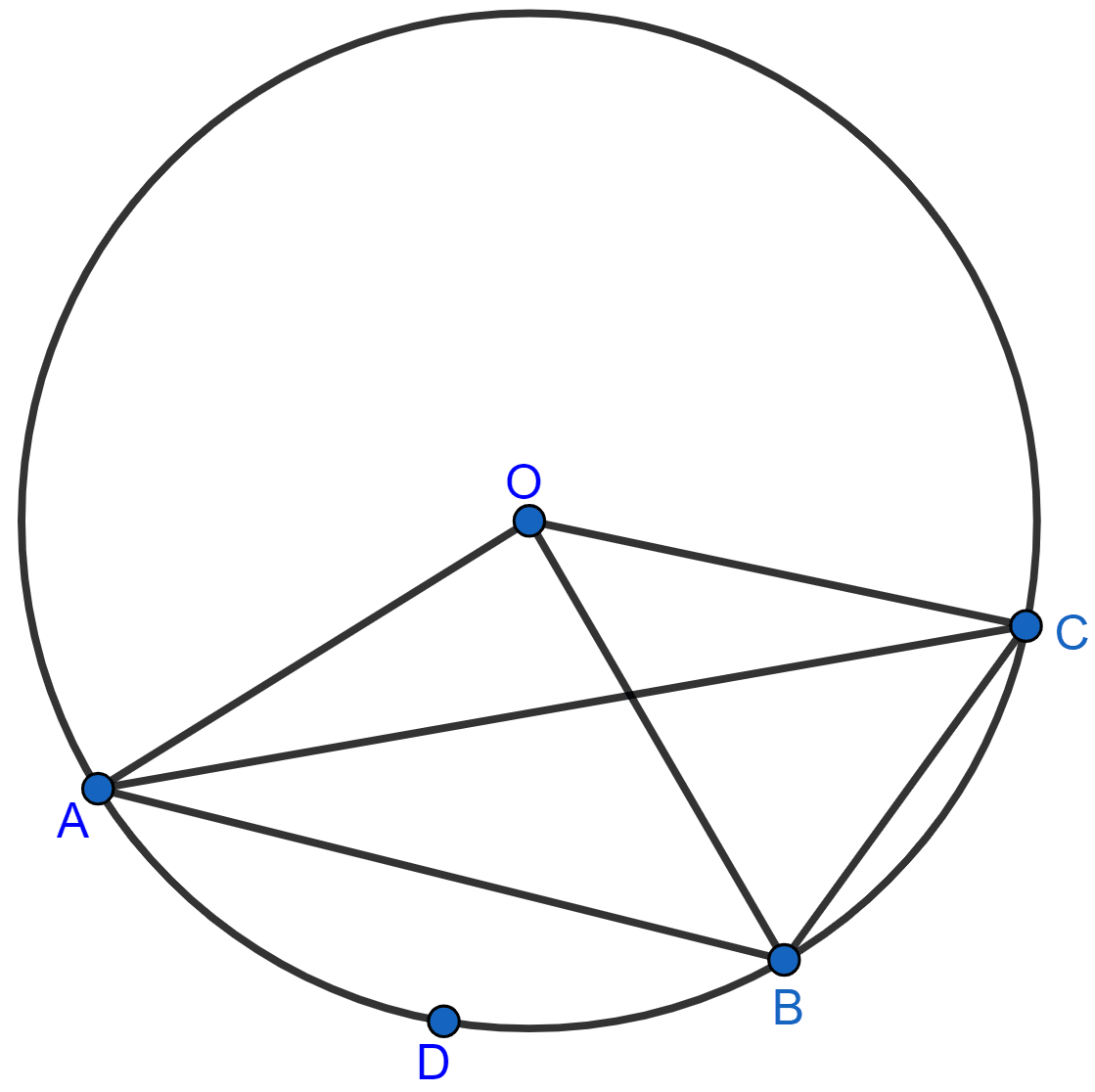
The figure shows a circle with centre O. AB is the side of regular pentagon and AC is the side of regular hexagon.
Find the angles of triangle ABC.

Circles
9 Likes
Answer
Join OA, OB and OC.

Since, AB is the side of regular pentagon,
∠AOB = = 72°.
Since, AC is the side of regular hexagon,
∠AOC = = 60°.
From figure,
⇒ ∠AOB + ∠AOC + reflex∠BOC = 360°
⇒ 72° + 60° + reflex∠BOC = 360°
⇒ reflex∠BOC + 132° = 360°
⇒ reflex∠BOC = 360° - 132° = 228°.
We know that,
Angle which an arc subtends at the center is double that which it subtends at any point on the remaining part of the circumference.
Arc BC subtends ∠BOC at the centre and ∠BAC at the remaining part of the circle.
∴ ∠BOC = 2∠BAC
⇒ ∠BAC = = 114°.
Arc AC subtends ∠AOC at the centre and ∠ABC at the remaining part of the circle.
∴ ∠AOC = 2∠ABC
⇒ ∠ABC = = 30°.
Arc AB subtends ∠AOB at the centre and ∠ACB at the remaining part of the circle.
∴ ∠AOB = 2∠ACB
⇒ ∠ACB = = 36°.
Hence, angles of triangle are ∠ABC = 30°, ∠ACB = 36° and ∠BAC = 114°.
Answered By
6 Likes
Related Questions
In the given figure, AB = BC = CD and ∠ABC = 132°. Calculate :
(i) ∠AEB,
(ii) ∠AED,
(iii) ∠COD.

In the figure, O is the centre of the circle and the length of arc AB is twice the length of arc BC. If angle AOB = 108°, find :
(i) ∠CAB,
(ii) ∠ADB.
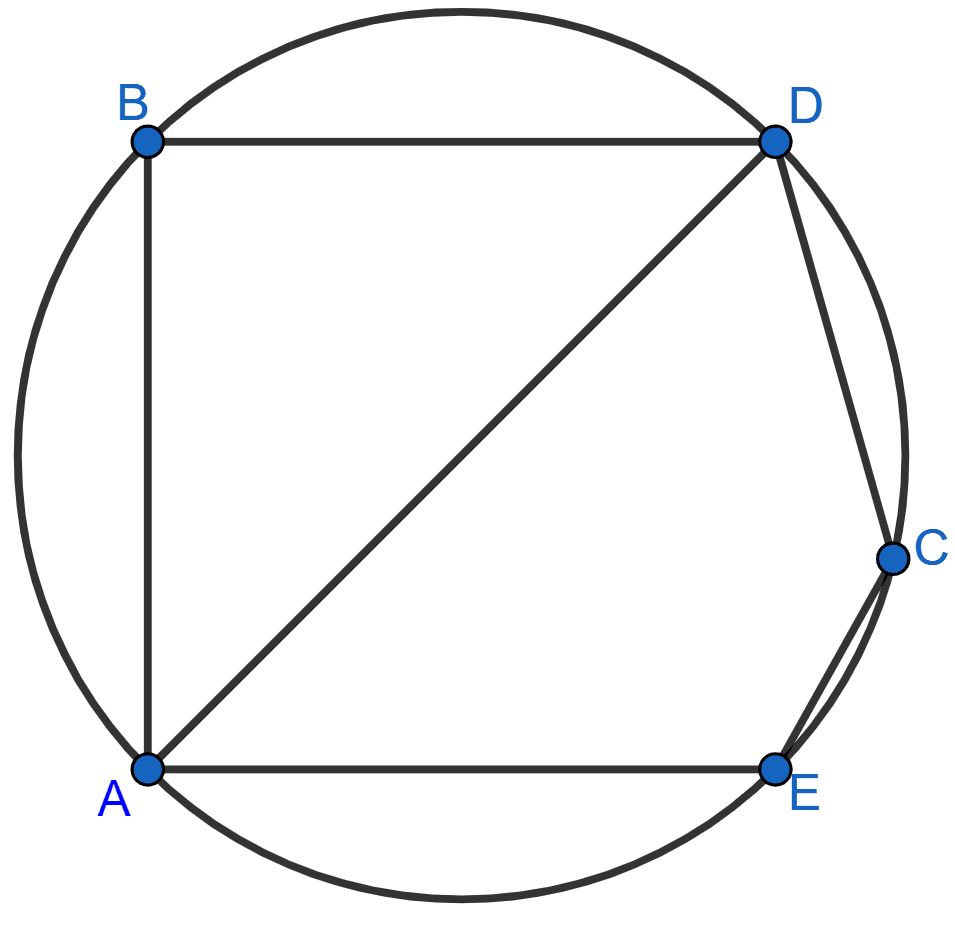
In the given figure, BD is a side of regular hexagon, DC is a side of a regular pentagon and AD is a diameter. Calculate :
(i) ∠ADC,
(ii) ∠BDA,
(iii) ∠ABC,
(iv) ∠AEC.
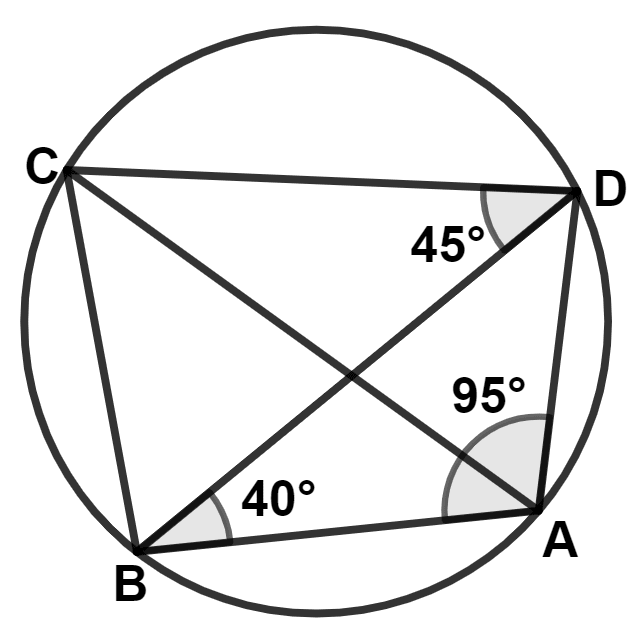
In the given circle, ∠BAD = 95°, ∠ABD = 40° and ∠BDC = 45°.
Assertion (A) : To show that AC is a diameter, the angle ADC or angle ABC need to be proved to be 90°.
Reason (R) : In △ADB,
∠ADB = 180° - 95° - 40° = 45°
∴ Angle ADC = 45° + 45° = 90°
(i) A is true, R is false
(ii) A is true, R is true
(iii) A is false, R is false
(iv) A is false, R is true