Mathematics
In the given figure, AB = BC = CD and ∠ABC = 132°. Calculate :
(i) ∠AEB,
(ii) ∠AED,
(iii) ∠COD.

Circles
17 Likes
Answer
(i) Join EB and EC.
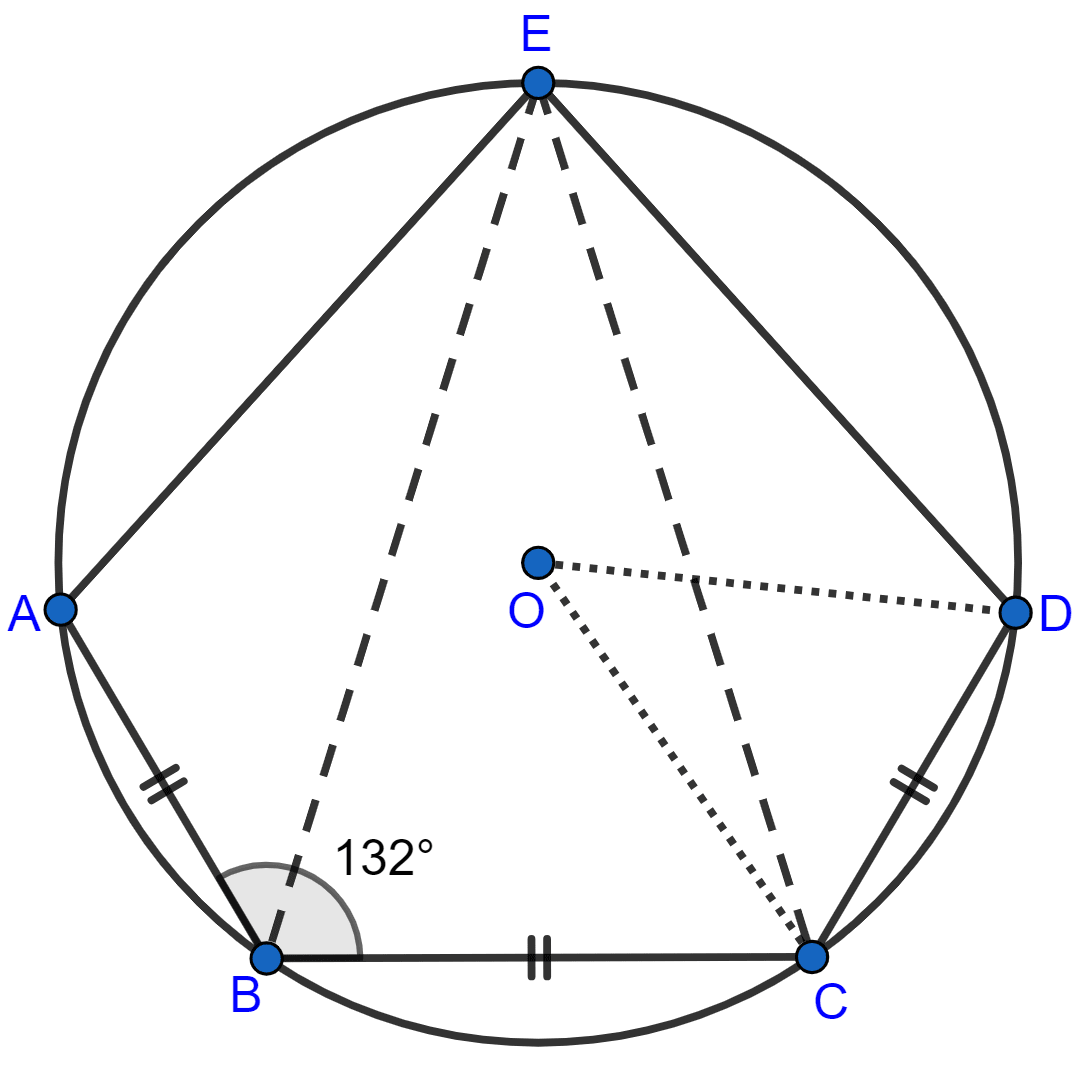
In cyclic quadrilateral ABCE,
⇒ ∠ABC + ∠AEC = 180° [Sum of opposite angles in cyclic quadrilateral = 180°]
⇒ 132° + ∠AEC = 180°
⇒ ∠AEC = 180° - 132° = 48°.
Since, AB = BC.
We know that,
Angle which an arc subtends at the center is double that which it subtends at any point on the remaining part of the circumference.
∴ ∠AEB = ∠AEC
= = 24°.
Hence, ∠AEB = 24°.
(ii) We know that,
Equal chords subtend equal angles at the circumference of the circle.
∠AEB = ∠BEC = ∠CED = 24°
∠AED = ∠AEB + ∠BEC + ∠CED = 24° + 24° + 24° = 72°.
Hence, ∠AED = 72°.
(iii) We know that,
Angle which an arc subtends at the center is double that which it subtends at any point on the remaining part of the circumference.
∴ ∠COD = 2∠CED = 2 × 24° = 48°.
Hence, ∠COD = 48°.
Answered By
9 Likes
Related Questions
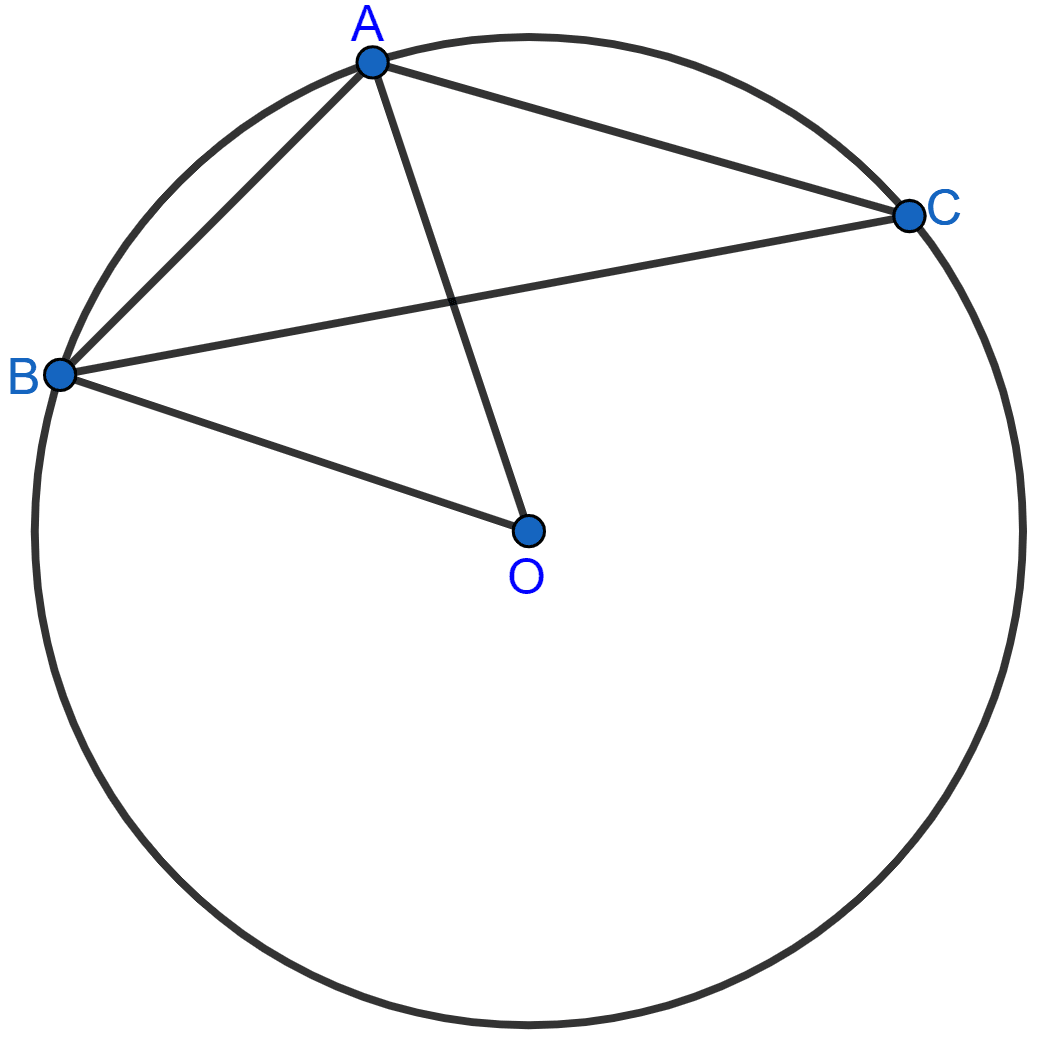
In the given figure, AB is a side of a regular six-sided polygon and AC is a side of a regular eight-sided polygon inscribed in the circle with centre O. Calculate the sizes of :
(i) ∠AOB,
(ii) ∠ACB,
(iii) ∠ABC.
In a regular pentagon ABCDE, inscribed in a circle; find the ratio between angle EDA and angle ADC.
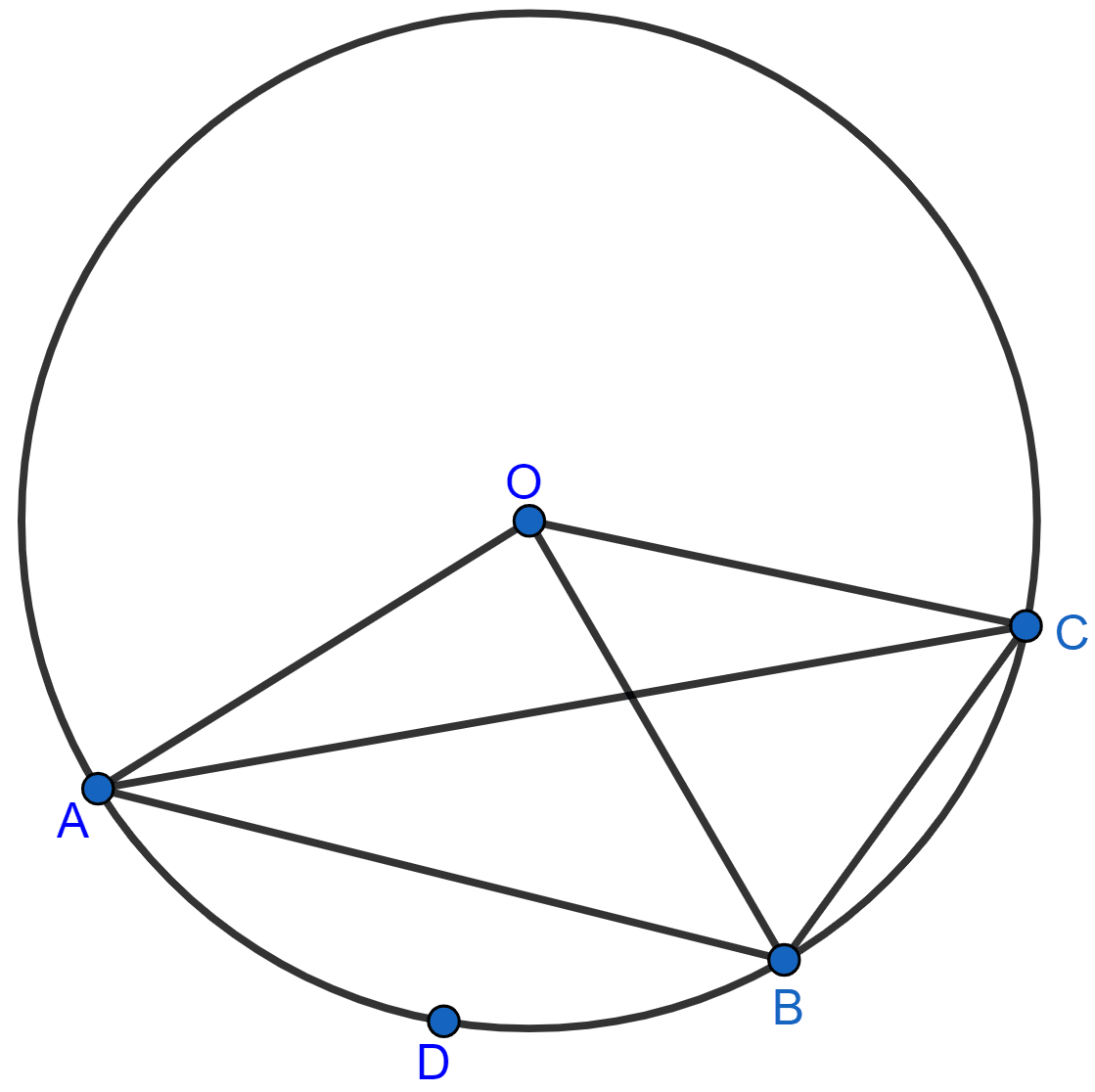
In the figure, O is the centre of the circle and the length of arc AB is twice the length of arc BC. If angle AOB = 108°, find :
(i) ∠CAB,
(ii) ∠ADB.
The figure shows a circle with centre O. AB is the side of regular pentagon and AC is the side of regular hexagon.
Find the angles of triangle ABC.
