Mathematics
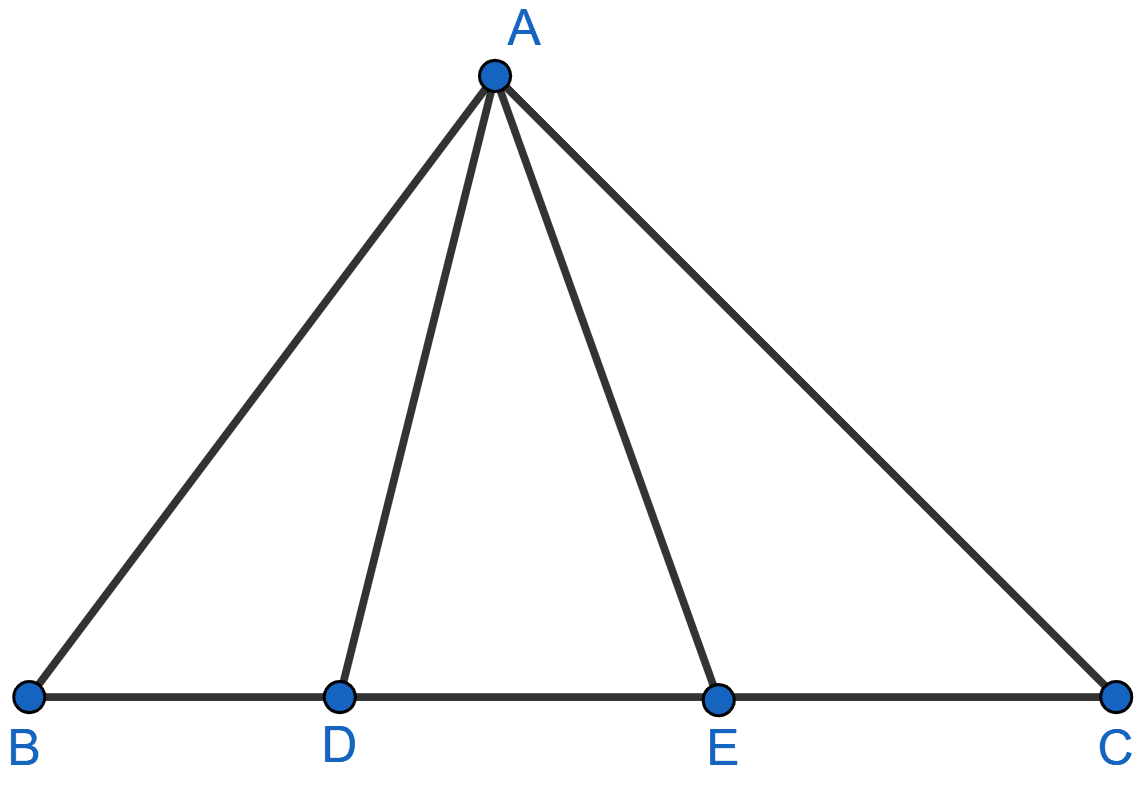
In the given figure, AD = AE and AD2 = BD x EC. Prove that: triangles ABD and CAE are similar.
Similarity
22 Likes
Answer
From figure,
⇒ ∠ADE = ∠AED [Angles opposite to equal sides of a triangle are equal].
⇒ 180° - ∠ADE = 180° - ∠AED
⇒ ∠ADB = ∠AEC
Given,
⇒ AD2 = BD x EC
⇒ AD x AD = BD x EC
⇒ AD x AE = BD x EC
⇒
∴ △ABD ~ △CAE [By SAS]
Hence, proved that △ABD ~ △CAE.
Answered By
12 Likes
Related Questions
In ΔABC, BM ⊥ AC and CN ⊥ AB; show that:
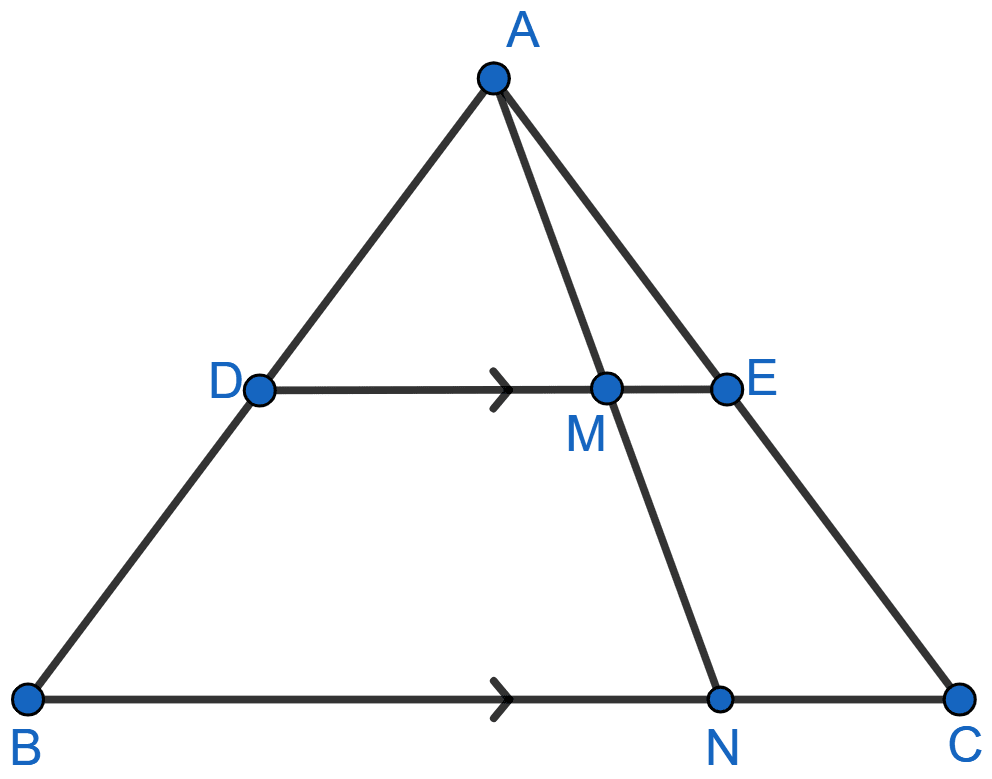
In the given figure, DE || BC, AE = 15 cm, EC = 9 cm, NC = 6 cm and BN = 24 cm.
(i) Write all possible pairs of similar triangles.
(ii) Find the lengths of ME and DM.
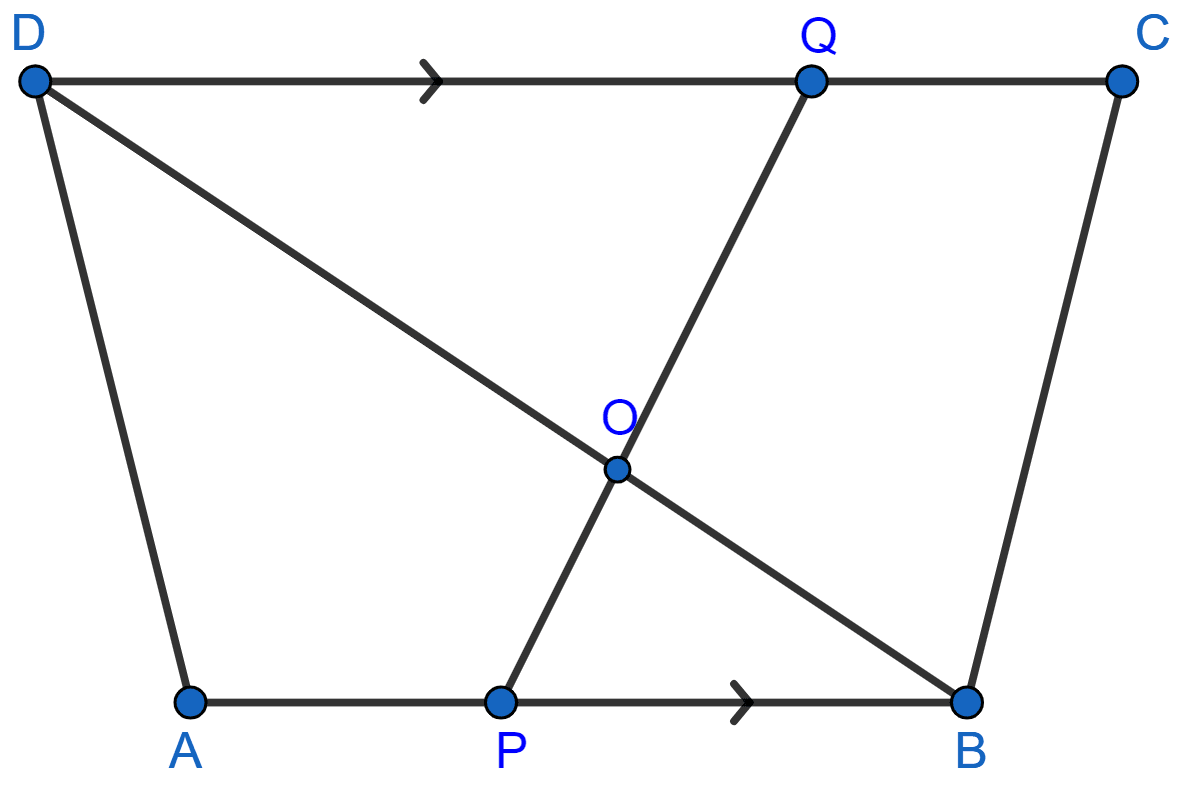
In the given figure, AB || DC, BO = 6 cm and DQ = 8 cm; find: BP x DO.
State, true or false:
(i) Two similar polygons are necessarily congruent.
(ii) Two congruent polygons are necessarily similar.
(iii) All equiangular triangles are similar.
(iv) All isosceles triangles are similar.
(v) Two isosceles-right triangles are similar.
(vi) Two isosceles triangles are similar, if an angle of one is congruent to the corresponding angle of the other.
(vii) The diagonals of a trapezium, divide each other into proportional segments.