Mathematics
In the given figure, AB is tangent to the circle with center O. If OCB is a straight line segment, the angle BAC is :
40°
55°
35°
20°

Circles
7 Likes
Answer
We know that,
Tangent at any point of a circle and the radius through this point are perpendicular to each other.
∴ OA ⊥ AB
∴ ∠OAB = 90°.
Let, ∠BAC = x
From figure,
In △OAC,
∠A = ∠OAB - ∠BAC = 90° - x.
Also,
OA = OC (Radius of same circle)
We know that,
Angles opposite to equal sides are equal.
∴ ∠C = ∠A = 90° - x.
By angle sum property of triangle,
⇒ ∠A + ∠O + ∠C = 180°
⇒ 90° - x + ∠O + 90° - x = 180°
⇒ ∠O + 180° - 2x = 180°
⇒ ∠O = 180° - 180° + 2x = 2x.
In △OAB,
By angle sum property of triangle,
⇒ ∠O + ∠A + ∠B = 180°
⇒ ∠O + ∠OAB + ∠B = 180°
⇒ 2x + 90° + 20° = 180°
⇒ 2x + 110° = 180°
⇒ 2x = 180° - 110°
⇒ 2x = 70°
⇒ x = = 35°.
⇒ ∠BAC = 35°.
Hence, Option 3 is the correct option.
Answered By
4 Likes
Related Questions
AP is a tangent to the given circle. If AB = 8 cm and BC = 10 cm, then AP is :
8 cm
16 cm
12 cm
24 cm

In the given figure, O is center of the circle and PQ is a tangent. If angle OAB = x; the measure of angle ABP; in terms of x, is :
x
180° - 2x
90° + x
90° - x

Two mutually perpendicular tangents are drawn to a circle with radius units. The shortest distance between the two points of contact is :
R units
units
units
2R units
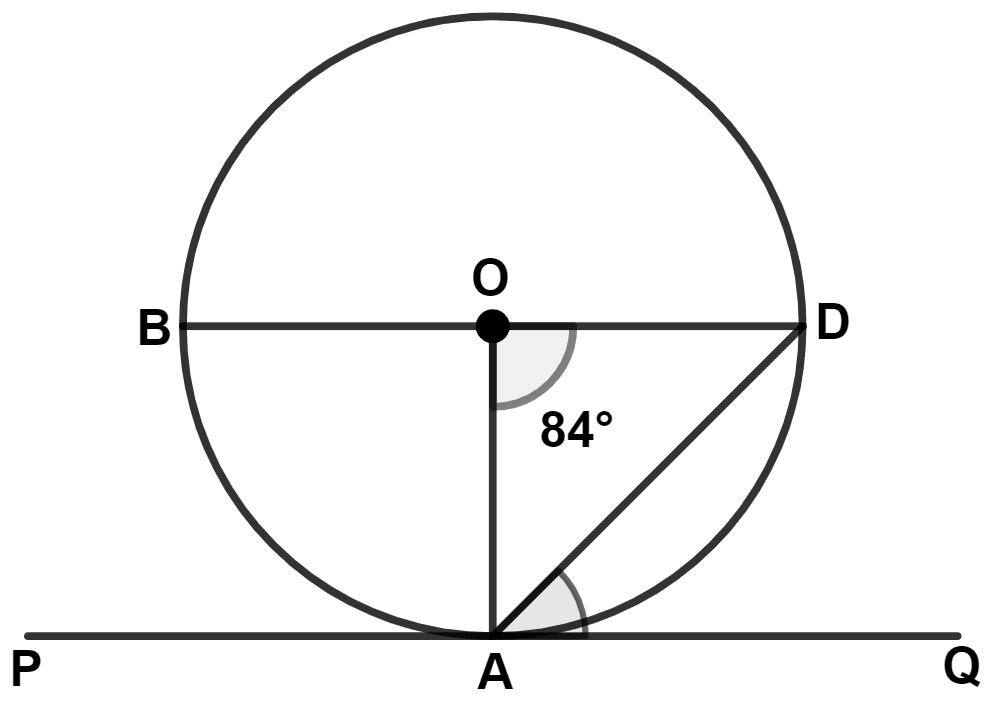
In the given figure O is center, PQ is tangent at point A. BD is diameter and ∠AOD = 84° then angle QAD is :
32°
84°
48°
42°