Mathematics
In the given figure, O is center of the circle and PQ is a tangent. If angle OAB = x; the measure of angle ABP; in terms of x, is :
x
180° - 2x
90° + x
90° - x

Circles
6 Likes
Answer
From figure,
In △OAB,
OA = OB (Radius of same circle)
We know that,
Angles opposite to equal sides are equal.
⇒ ∠OBA = ∠OAB = x
We know that,
Tangent at any point of a circle and the radius through this point are perpendicular to each other.
∴ OB ⊥ PQ
∴ ∠PBO = 90°
From figure,
∠ABP = ∠PBO - ∠OBA = 90° - x.
Hence, Option 4 is the correct option.
Answered By
4 Likes
Related Questions
In the adjoining figure, O is the center of the circle and AB is a tangent to it at point B. ∠BDC = 65°. Find ∠BAO.

AP is a tangent to the given circle. If AB = 8 cm and BC = 10 cm, then AP is :
8 cm
16 cm
12 cm
24 cm

In the given figure, AB is tangent to the circle with center O. If OCB is a straight line segment, the angle BAC is :
40°
55°
35°
20°

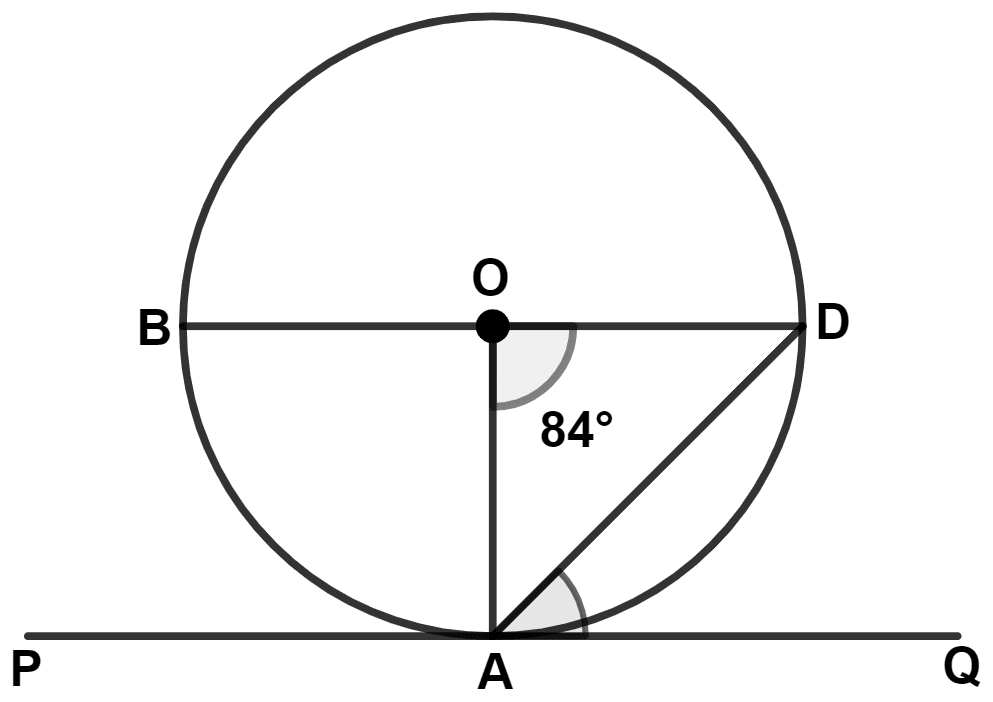
In the given figure O is center, PQ is tangent at point A. BD is diameter and ∠AOD = 84° then angle QAD is :
32°
84°
48°
42°