Mathematics
Two mutually perpendicular tangents are drawn to a circle with radius units. The shortest distance between the two points of contact is :
R units
units
units
2R units
Circles
9 Likes
Answer
Let two perpendicular tangents from external point A touch the circle at points B and C.
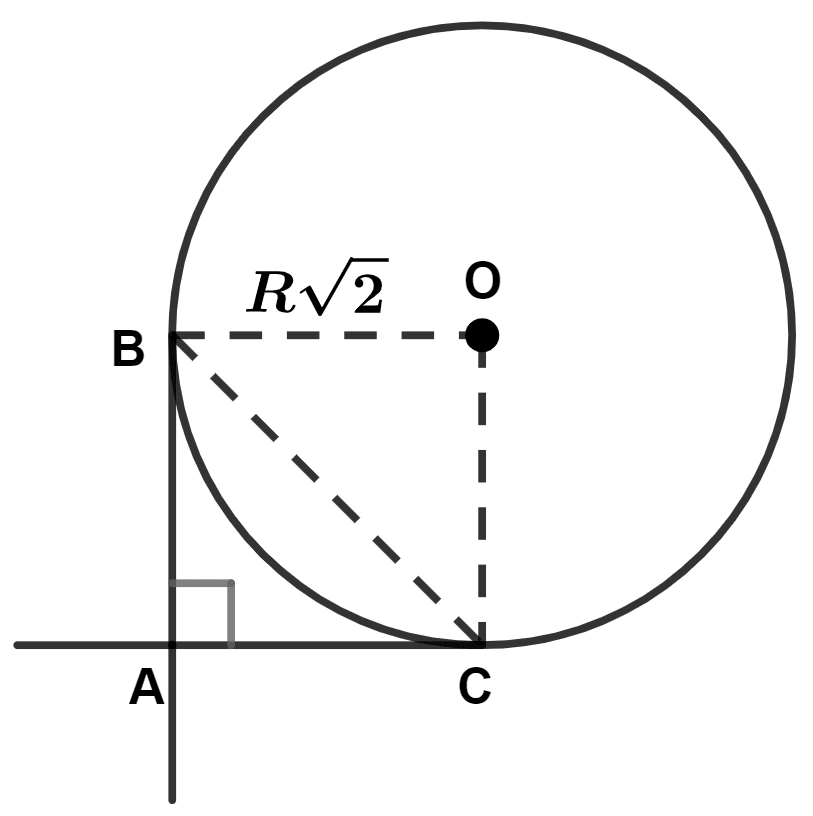
Given,
Radius = units
From figure,
AC = OB = ,
AB = OC = .
In right angle triangle ABC,
⇒ BC2 = AB2 + AC2
⇒ BC2 =
⇒ BC2 = 2R2 + 2R2
⇒ BC2 = 4R2
⇒ BC =
⇒ BC = 2R units.
Hence, Option 4 is the correct option.
Answered By
4 Likes
Related Questions
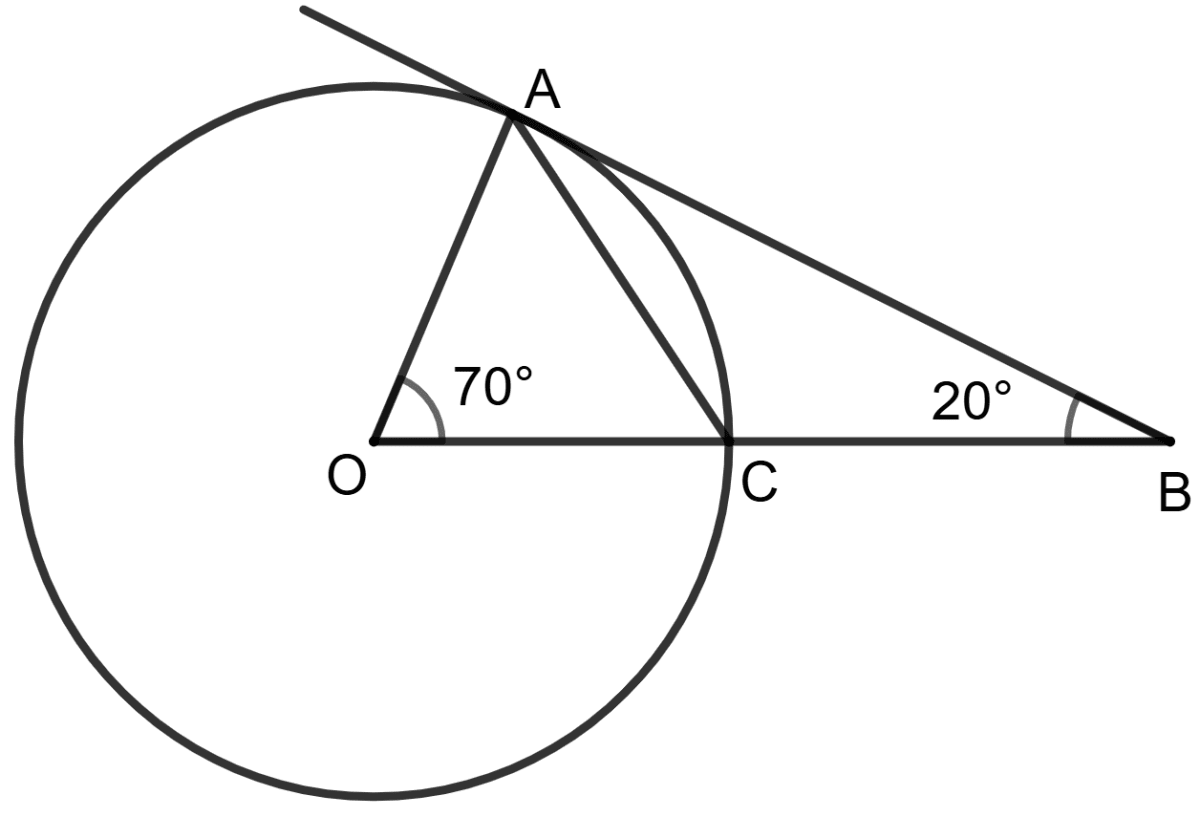
In the given figure, AB is tangent to the circle with center O. If OCB is a straight line segment, the angle BAC is :
40°
55°
35°
20°
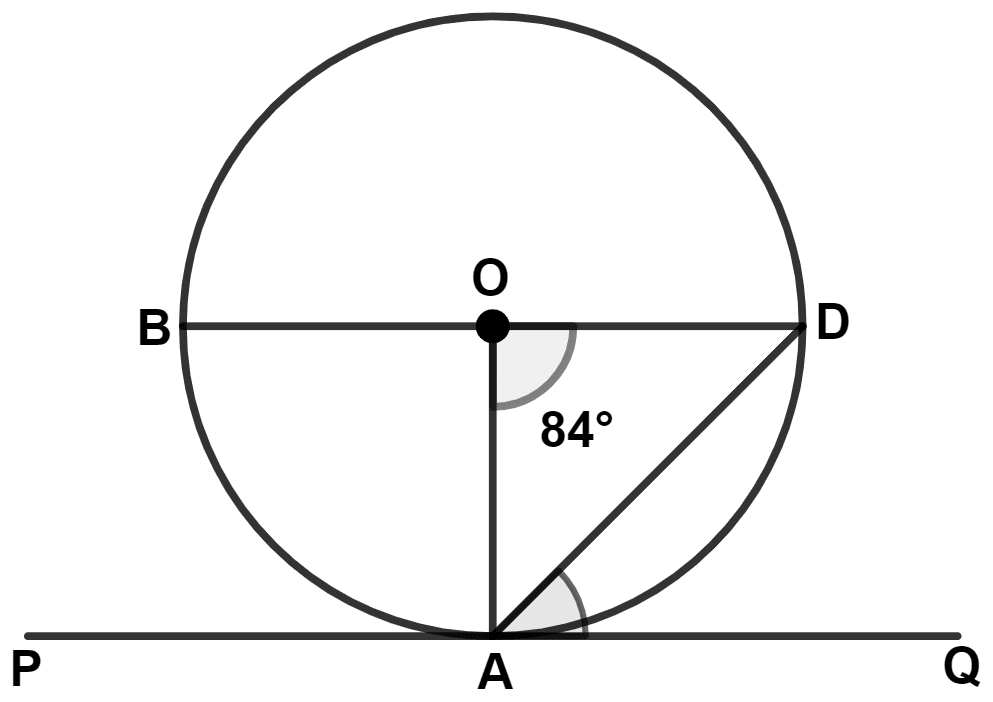
In the given figure O is center, PQ is tangent at point A. BD is diameter and ∠AOD = 84° then angle QAD is :
32°
84°
48°
42°
For the three circles with centers A, B and C and radii 5 cm, 2 cm and 6 cm respectively.
Assertion (A) : To find the perimeter of the triangle ABC, add the radii of given three circles.
Reason (R) : The required perimeter is the product of sum of radii by 2.
A is true, R is true
A is true, R is false
A is false, R is true
A is false, R is false
AB is diameter of the circle. PA is tangent and ∠AOC = 60°.
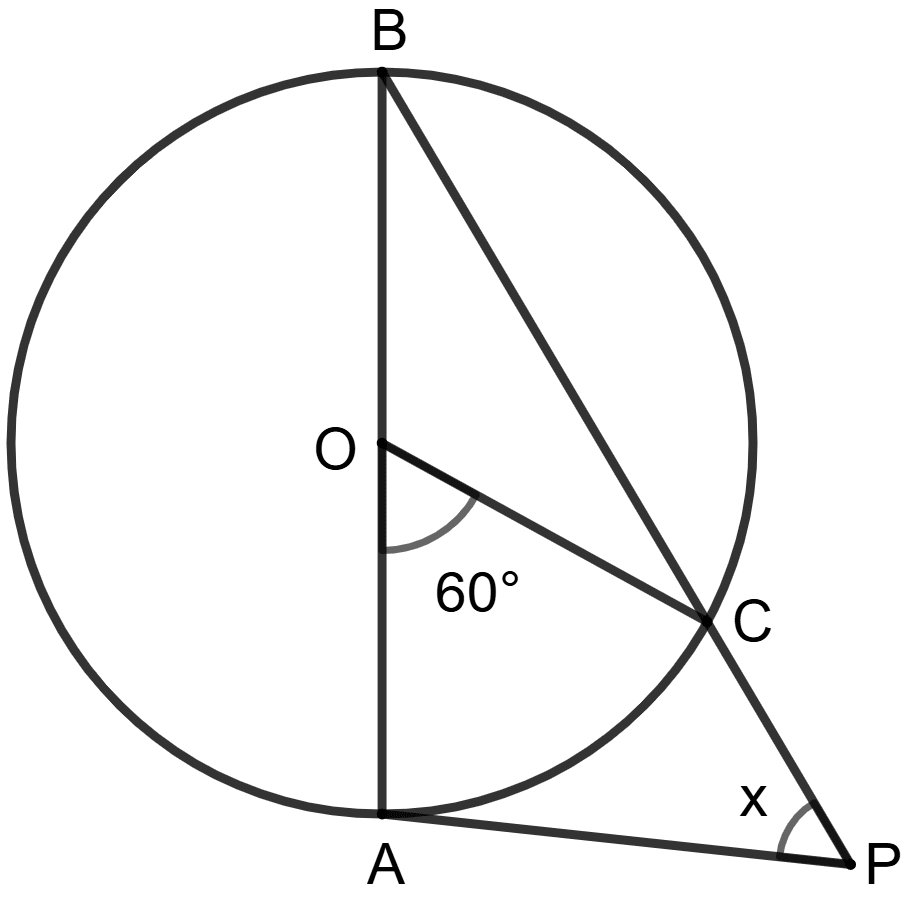
Assertion(A): x + 30° = 90°.
Reason(R): PA is tangent
⇒ ∠BAP = 90°
∴ x + 30° = 90°
A is true, R is false.
A is false, R is true.
Both A and R are true and R is correct reason for A.
Both A and R are true and R is incorrect reason for A.