Mathematics

Prove that, of any two chords of a circle, the greater chord is nearer to the centre.

21 Likes

Let there be a circle with center O and radius r. AB and CD are two chords of this circle. OM < ON where OM ⊥ AB and ON ⊥ CD.

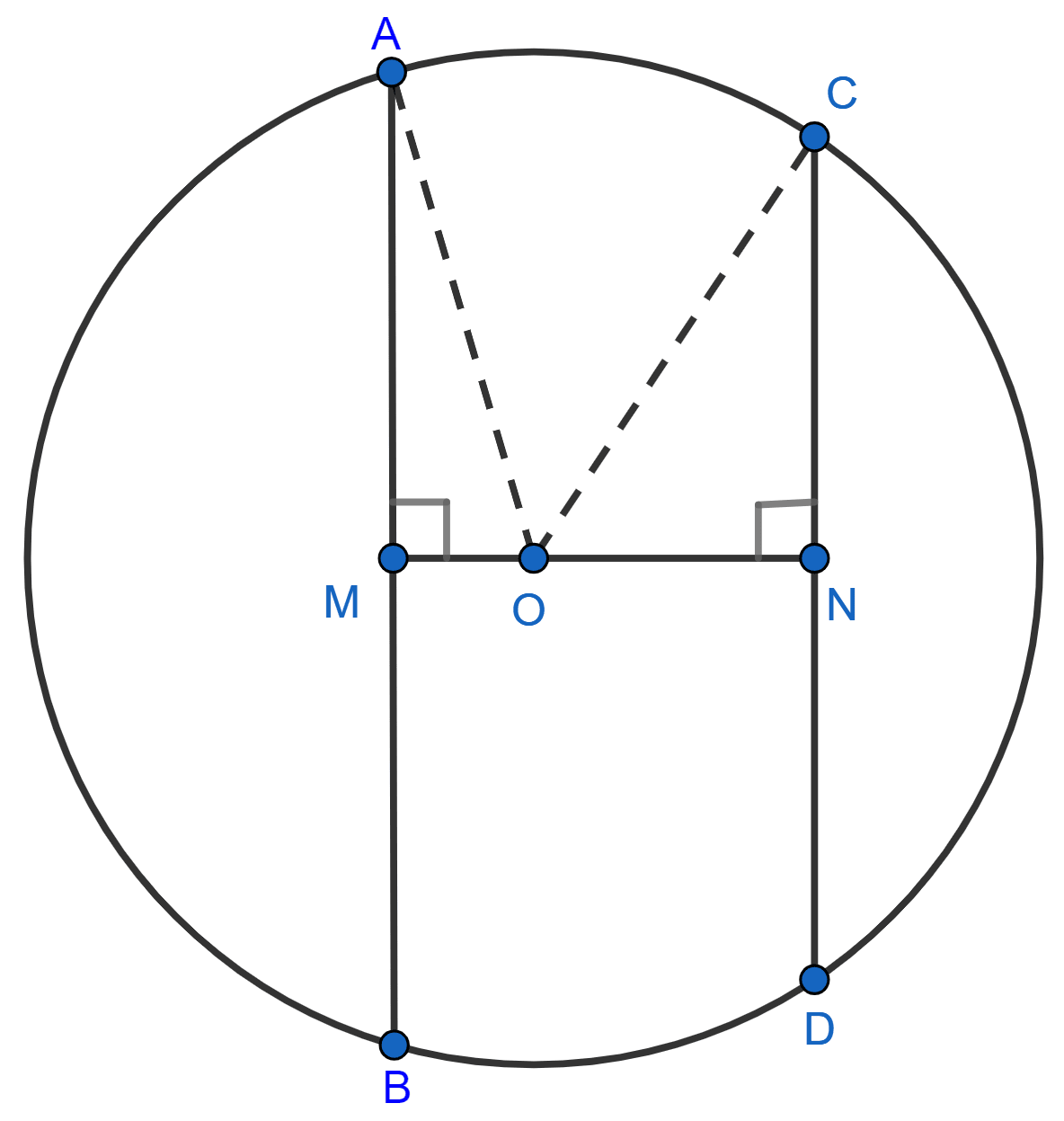
To prove: AB > CD

We know that,

The perpendicular from the centre of a circle to a chord bisects the chord.

∴ AM = $\dfrac{AB}{2}$ and CN = $\dfrac{CD}{2}$

Join OA and OC.

In right angle triangle OAM,

⇒ OA² = AM² + OM²

⇒ AM² = OA² - OM² ….. (1)

In right angle triangle ONC,

⇒ OC² = CN² + ON²

⇒ CN² = OC² - ON² ….. (2)

OM < ON

⇒ OM² < ON²

⇒ -OM² > -ON²

⇒ OA² - OM² > OC² - ON² [∵ OA = OC]

⇒ AM² > CN² [From (1) and (2)]

⇒ $\Big(\dfrac{\text{AB}}{2}\Big)^2$ > $\Big(\dfrac{\text{CD}}{2}\Big)^2$

⇒ $\dfrac{1}{4}$ AB² > $\dfrac{1}{4}$ CD²

⇒ AB² > CD²

⇒ AB > CD

Hence proved that, of any two chords of a circle, the greater chord is nearer to the centre.

Answered By

10 Likes