Mathematics
ABCD is a cyclic quadrilateral in which BC is parallel to AD, angle ADC = 110° and angle BAC = 50°. Find angle DAC and angle DCA.
Circles
13 Likes
Answer
Given, ABCD is a cyclic quadrilateral in which AD || BC
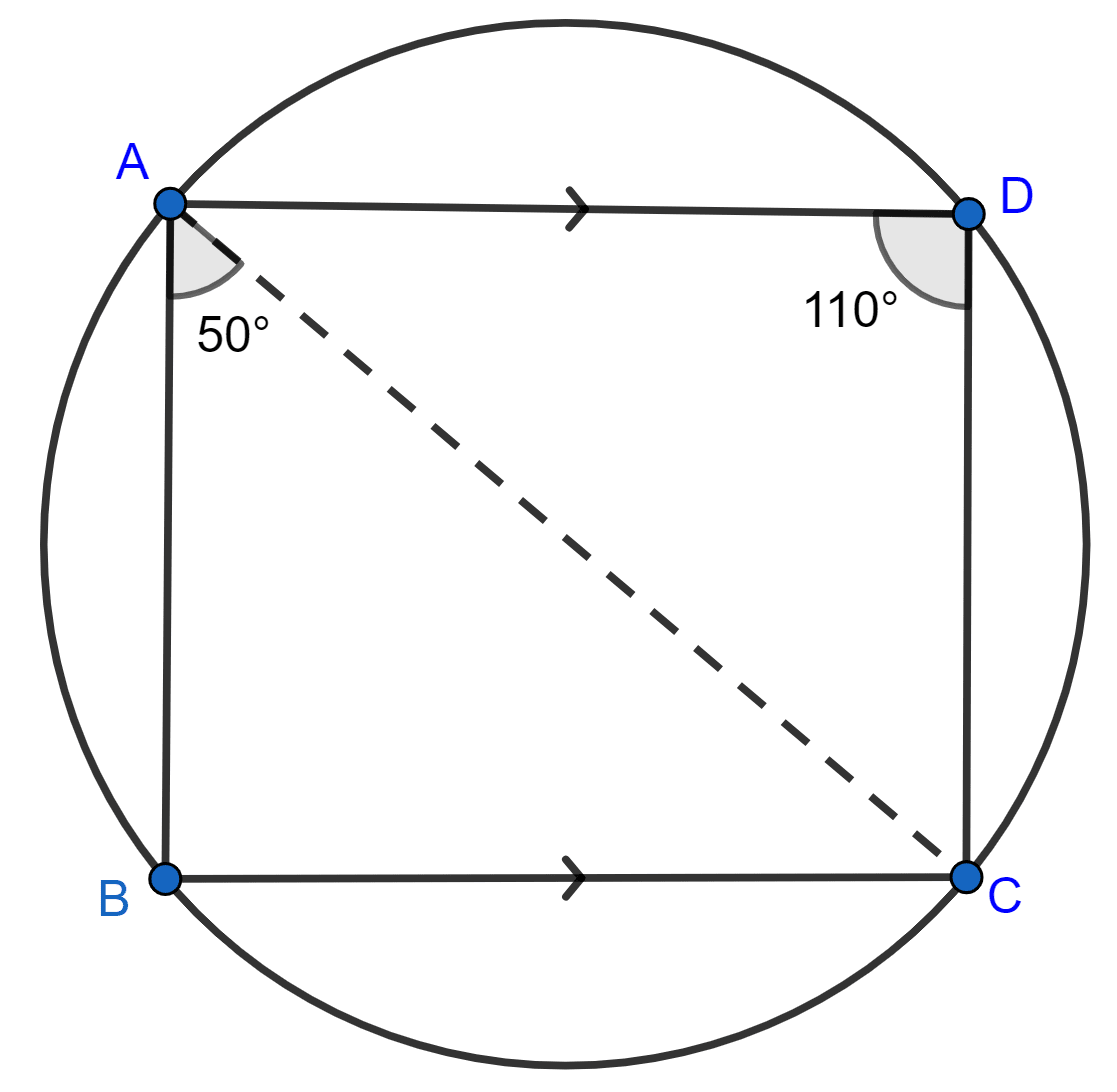
With, ∠ADC = 110°, ∠BAC = 50°.
We know that,
⇒ ∠B + ∠D = 180° [Sum of opposite angles of a cyclic quadrilateral = 180°]
⇒ ∠B + 110° = 180°
⇒ ∠B = 180° - 110°
⇒ ∠B = 70°.
Now in ∆ABC, we have
⇒ ∠BAC + ∠ABC + ∠ACB = 180° [By angle sum property of triangle]
⇒ 50° + 70° + ∠ACB = 180°
⇒ ∠ACB = 180° - 120° = 60°
As, AD || BC we have
∠DAC = ∠ACB = 60° [Alternate angles]
Now in ∆ADC,
⇒ ∠DAC + ∠ADC + ∠DCA = 180°
⇒ 60° + 110° + ∠DCA = 180°
⇒ ∠DCA = 180° - 170° = 10°
Hence, ∠DAC = 60° and ∠DCA = 10°.
Answered By
12 Likes
Related Questions
For the three circles with centers A, B and C and radii 5 cm, 2 cm and 6 cm respectively.
Assertion (A) : To find the perimeter of the triangle ABC, add the radii of given three circles.
Reason (R) : The required perimeter is the product of sum of radii by 2.
A is true, R is true
A is true, R is false
A is false, R is true
A is false, R is false
Prove that, of any two chords of a circle, the greater chord is nearer to the centre.
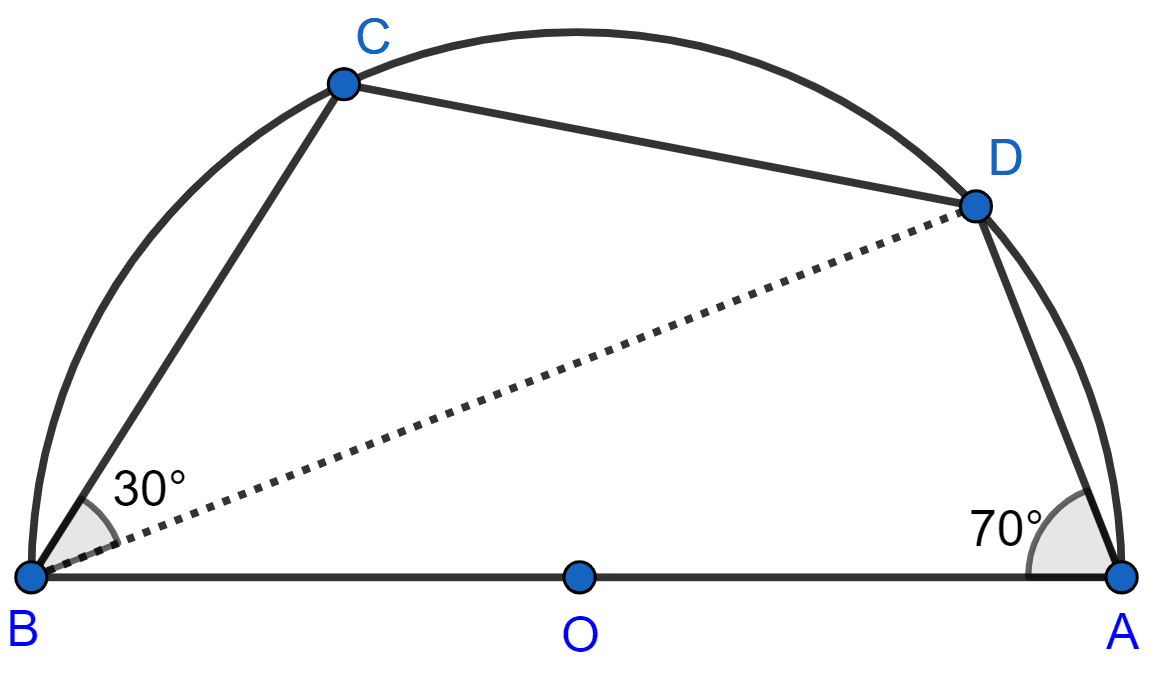
In the given figure, C and D are points on the semi-circle described on AB as diameter.
Given angle BAD = 70° and angle DBC = 30°, calculate angle BDC.
In cyclic quadrilateral ABCD, ∠A = 3∠C and ∠D = 5∠B. Find the measure of each angle of the quadrilateral.