Mathematics
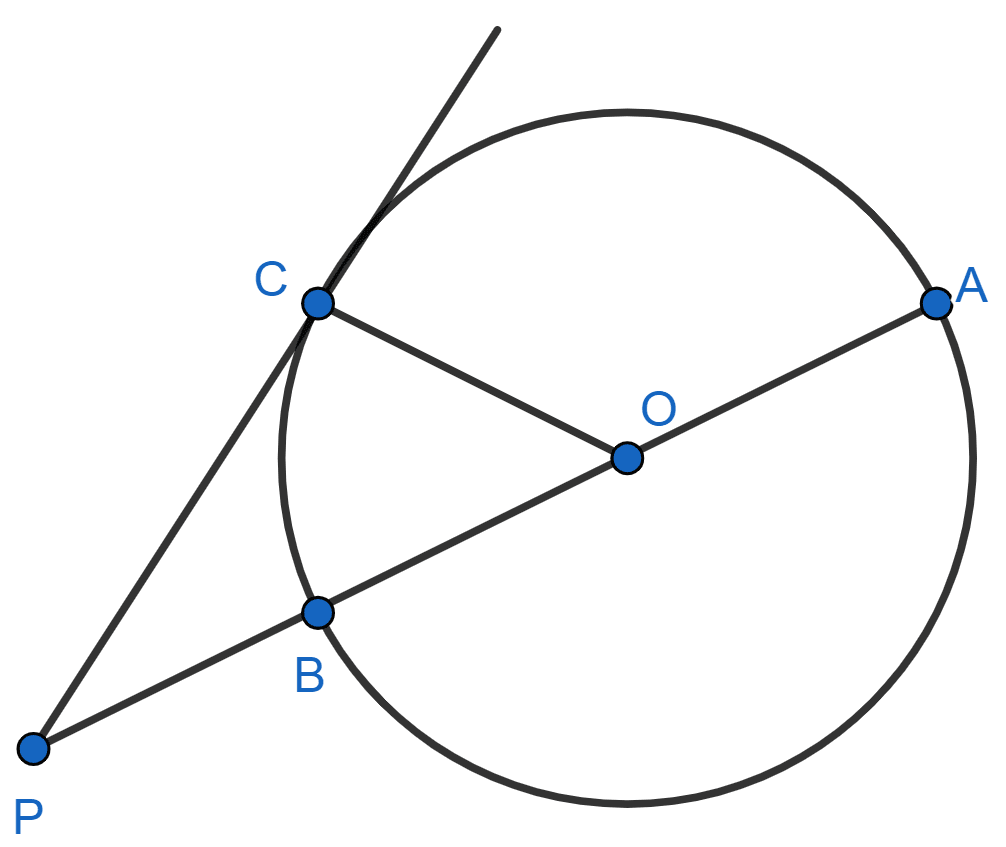
In the given figure, AB is diameter and PC is tangent to the circle with center O. If AP = 40 cm, CP = 20 cm, find the radius of the circle.
Circles
3 Likes
Answer
Let radius of circle be r cm.
From figure,
⇒ AP = AB + BP
⇒ 40 = AO + OB + BP
⇒ 40 = r + r + BP
⇒ 40 = 2r + BP
⇒ BP = (40 - 2r) cm.
We know that,
Tangent at point of intersection and radius of circle are perpendicular to each other.
In △OCP,
⇒ OP2 = OC2 + PC2
⇒ (OB + BP)2 = OC2 + PC2
⇒ (r + 40 - 2r)2 = r2 + 202
⇒ (40 - r)2 = r2 + 400
⇒ 1600 + r2 - 80r = r2 + 400
⇒ r2 - r2 + 80r = 1600 - 400
⇒ 80r = 1200
⇒ r = = 15 cm.
Hence, radius of circle = 15 cm.
Answered By
3 Likes
Related Questions
The following table shows the distribution of the marks obtained by 50 students in an aptitude test.
Marks obtained No. of students 15 6 18 18 21 12 24 8 27 4 30 2 Find the mean, the median and the mode of the distribution.
If }[r] x & 6 \ y & 8 \end{bmatrix} + 3 \times \begin{bmatrix}[r] 1 & -1 \ 0 & 2 \end{bmatrix} = 3 \times \begin{bmatrix}[r] 3 & 3 \ 4 & 6 \end{bmatrix}, find the values of x and y.
Using remainder theorem, factorise 6x3 - 11x2 - 3x + 2 completely.
In rhombus ABCD, the co-ordinates of point A and C are (2, -6) and (-4, 8) respectively. Find the equation of the diagonal BD.