Mathematics
In the given figure, AB and DE are perpendiculars to BC.
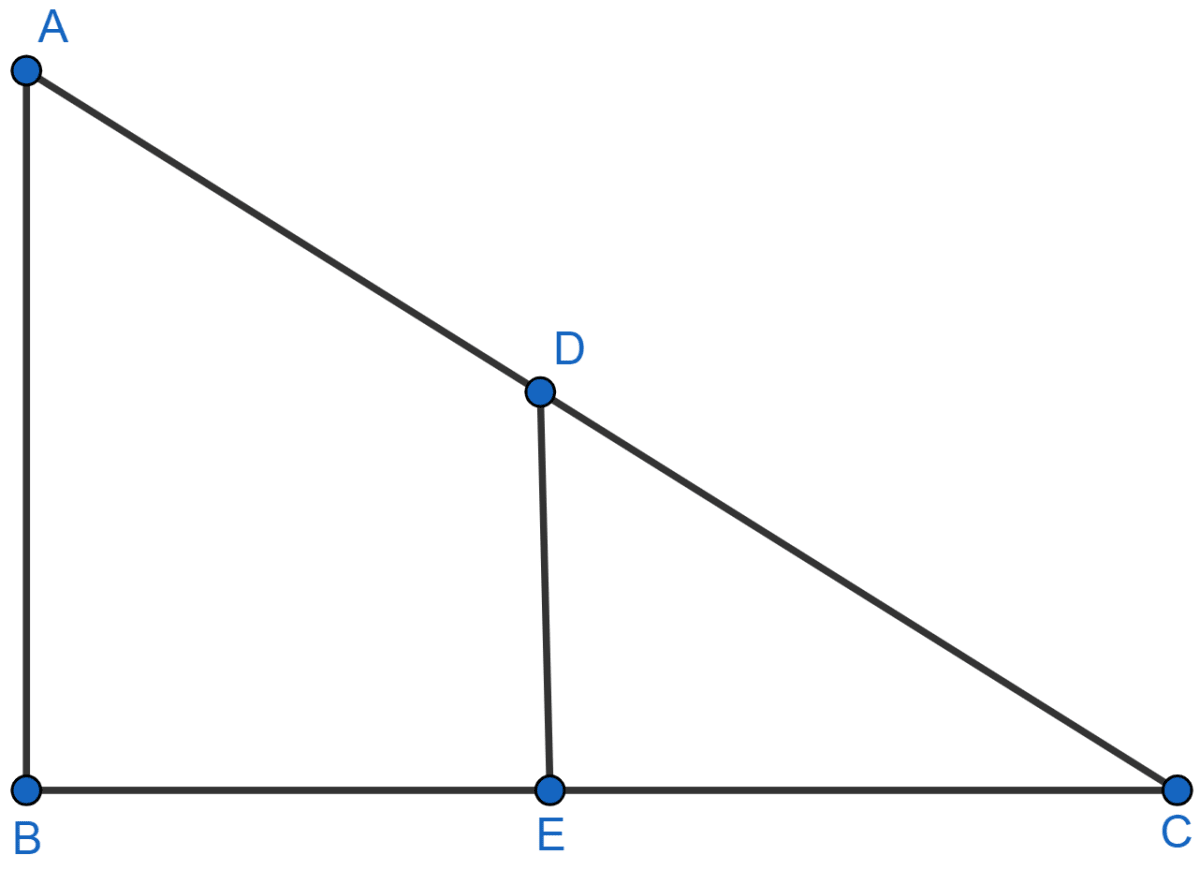
(i) Prove that △ABC ~ △DEC.
(ii) If AB = 6 cm, DE = 4 cm and AC = 15 cm, calculate CD.
(iii) Find the ratio of the area of △ABC : area of △DEC.
Similarity
Answer
(i) Considering △DEC and △ABC,
∠ C = ∠ C (Common angles)
∠ ABC = ∠ DEC (Both angles are equal to 90°)
Hence, by AA axiom △DEC ~ △ABC.
(ii) Since △DEC ~ △ABC, so, ratio of their corresponding sides will be equal
Hence, the length of CD = 10 cm.
(iii) We know that, the ratio of the areas of two similar triangles is equal to the ratio of the square of their corresponding sides.
Hence, the ratio of the area of △ABC : area of △DEC = 9 : 4.
Answered By
Related Questions
In the figure (ii) given below, DE || BC and AD : DB = 1 : 2, find the ratio of the areas of △ADE and trapezium DBCE.

In the given figure, DE || BC.

(i) Prove that △ADE and △ABC are similar.
(ii) Given that AD = BD, calculate DE, if BC = 4.5 cm.
(iii) If area of △ABC = 18 cm2, find area of trapezium DBCE.
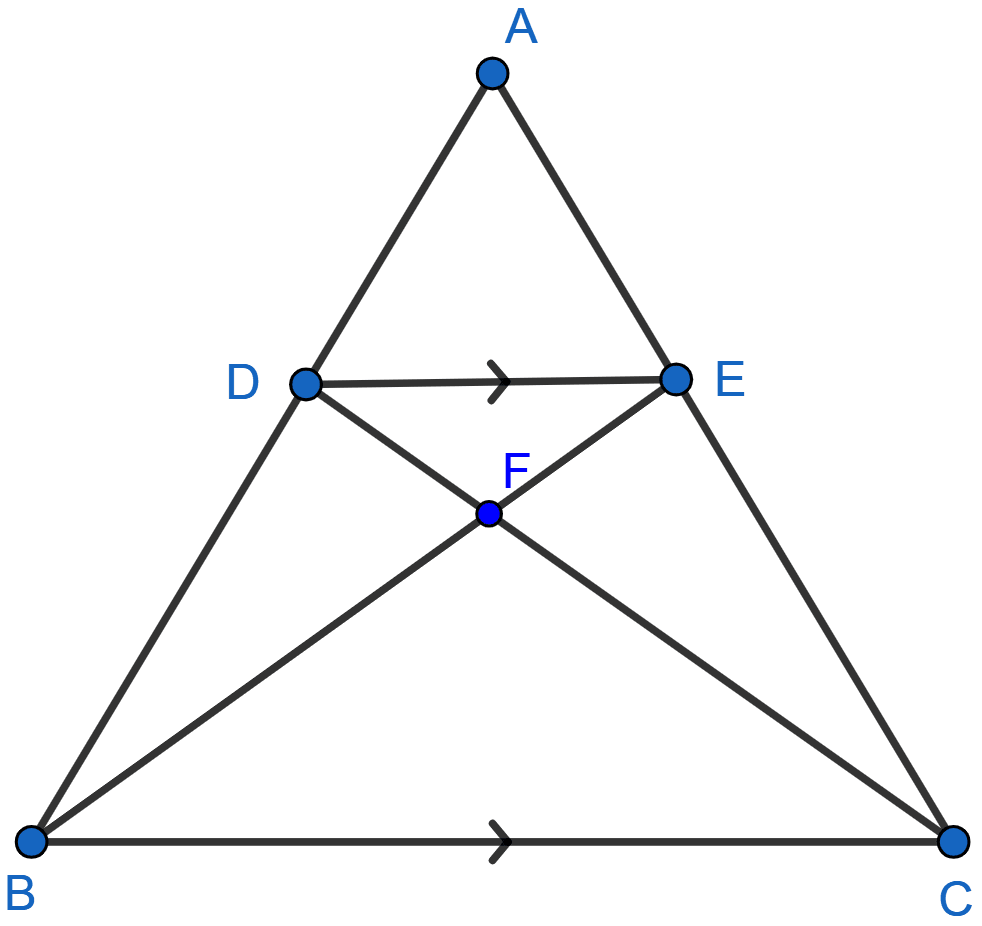
In the adjoining figure, ABC is a triangle. DE is parallel to BC and
(i) Determine the ratio
(ii) Prove that △DEF is similar to △CBF. Hence, find
(iii) What is the ratio of the areas of △DEF and △CBF ?
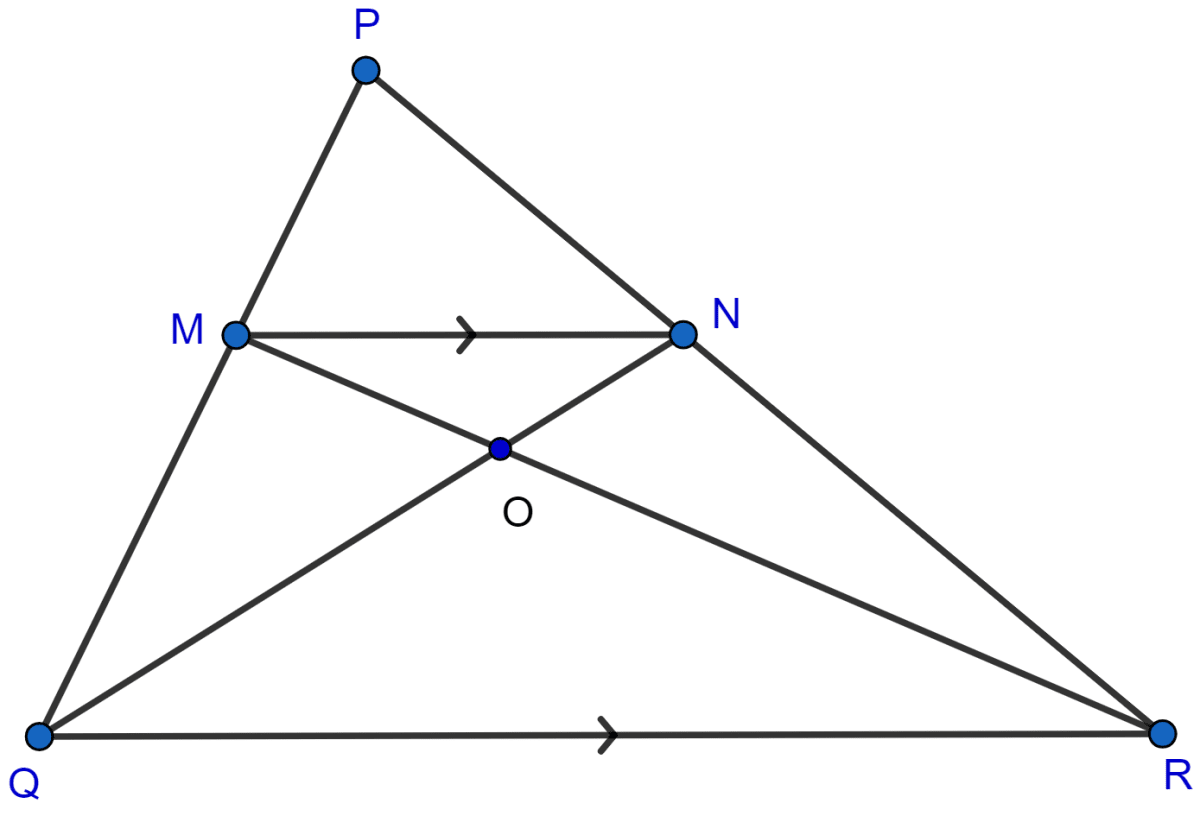
In △PQR, MN is parallel to QR and
(i) Find .
(ii) Prove that △OMN and △ORQ are similar.
(iii) Find area of △OMN : area of △ORQ.