Mathematics
In the figure (ii) given below, DE || BC and AD : DB = 1 : 2, find the ratio of the areas of △ADE and trapezium DBCE.

Similarity
59 Likes
Answer
Considering △ADE and △ABC,
∠ A = ∠ A (Common angles)
∠ ADE = ∠ ABC (Corresponding angles are equal)
Hence, by AA axiom △ADE ~ △ABC.
Given AD : DB = 1 : 2.
We know that, the ratio of the areas of two similar triangles is equal to the ratio of the square of their corresponding sides.
Hence, the ratio of the areas of △ADE and trapezium DBCE is 1 : 8.
Answered By
34 Likes
Related Questions
In the figure (ii) given below, AB || DC. AO = 10 cm, OC = 5 cm, AB = 6.5 cm and OD = 2.8 cm.

(i) Prove that △OAB ~ △OCD.
(ii) Find CD and OB.
(iii) Find the ratio of areas of △OAB and △OCD.
In the figure (i) given below, DE || BC. If DE = 6 cm, BC = 9 cm and area of △ADE = 28 sq. cm, find the area of △ABC.

In the given figure, DE || BC.

(i) Prove that △ADE and △ABC are similar.
(ii) Given that AD = BD, calculate DE, if BC = 4.5 cm.
(iii) If area of △ABC = 18 cm2, find area of trapezium DBCE.
In the given figure, AB and DE are perpendiculars to BC.
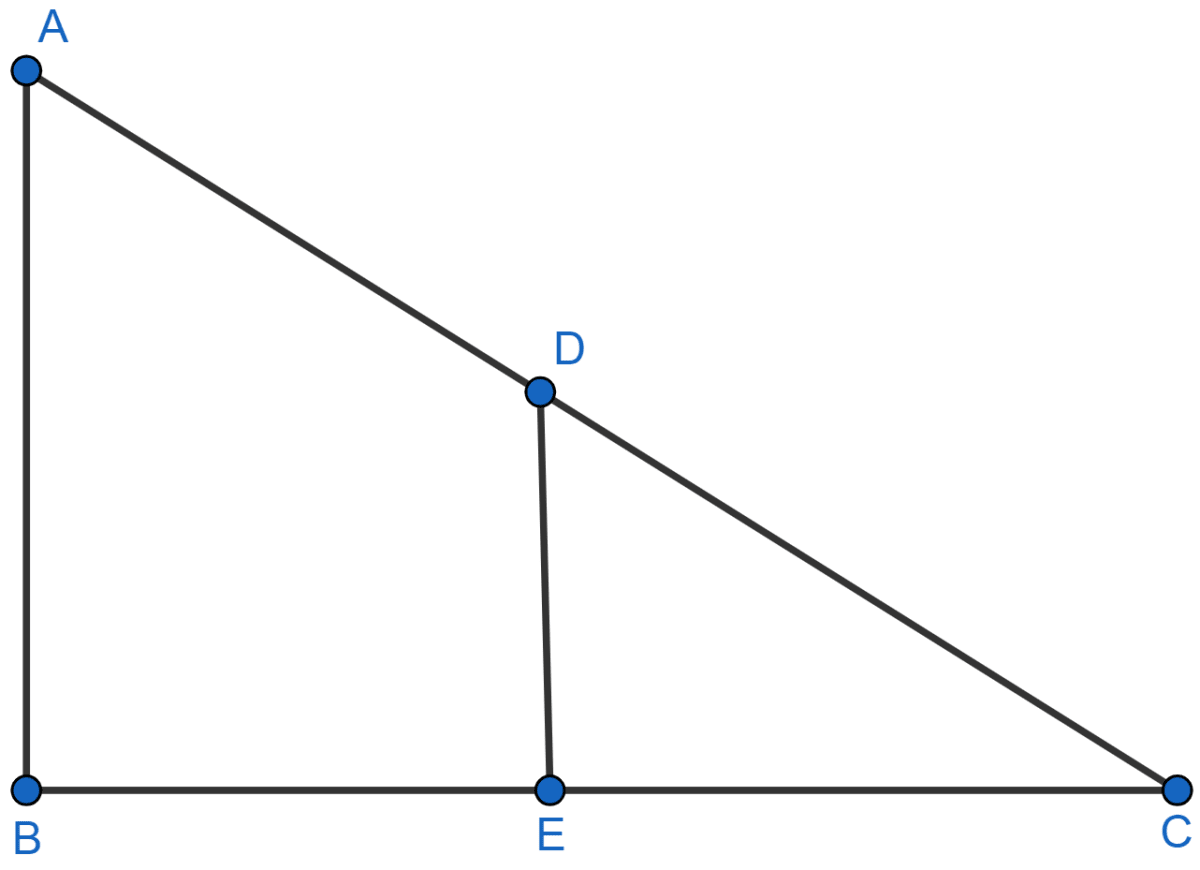
(i) Prove that △ABC ~ △DEC.
(ii) If AB = 6 cm, DE = 4 cm and AC = 15 cm, calculate CD.
(iii) Find the ratio of the area of △ABC : area of △DEC.