Mathematics
In the adjoining figure, ABC is a triangle. DE is parallel to BC and
(i) Determine the ratio
(ii) Prove that △DEF is similar to △CBF. Hence, find
(iii) What is the ratio of the areas of △DEF and △CBF ?
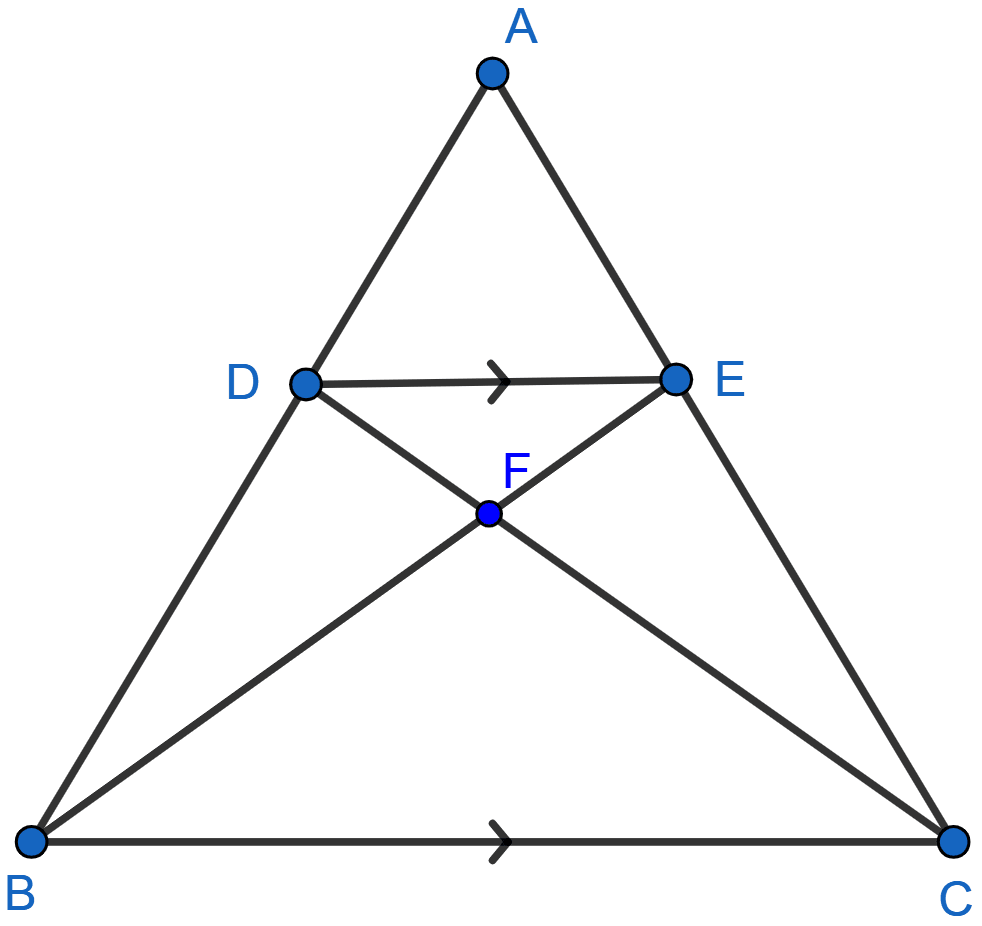
Similarity
29 Likes
Answer
(i) We need to find ,
Given,
Hence, the ratio .
Considering △ADE and △ABC,
∠ A = ∠ A (Common angles)
∠ ADE = ∠ ABC (Corresponding angles are equal)
Hence, by AA axiom △ADE ~ △ABC.
Since triangles ADE and ABC are similar so the ratio of corresponding sides will be equal.
Hence, the ratio .
(ii) Considering △DEF and △CBF,
∠ DFE = ∠ BFC (Vertically opposite angles)
∠ EDF = ∠ FCB (Alternate angles are equal)
Hence, by AA axiom △DEF ~ △CBF.
Since triangles are similar hence the ratio of the corresponding sides will be equal,
Hence, the value of
(iii) We know that, the ratio of the areas of two similar triangles is equal to the ratio of the square of their corresponding sides.
Hence, the ratio of the area of △DEF : area of △CBF = 9 : 25.
Answered By
17 Likes
Related Questions
In the given figure, DE || BC.

(i) Prove that △ADE and △ABC are similar.
(ii) Given that AD = BD, calculate DE, if BC = 4.5 cm.
(iii) If area of △ABC = 18 cm2, find area of trapezium DBCE.
In the given figure, AB and DE are perpendiculars to BC.
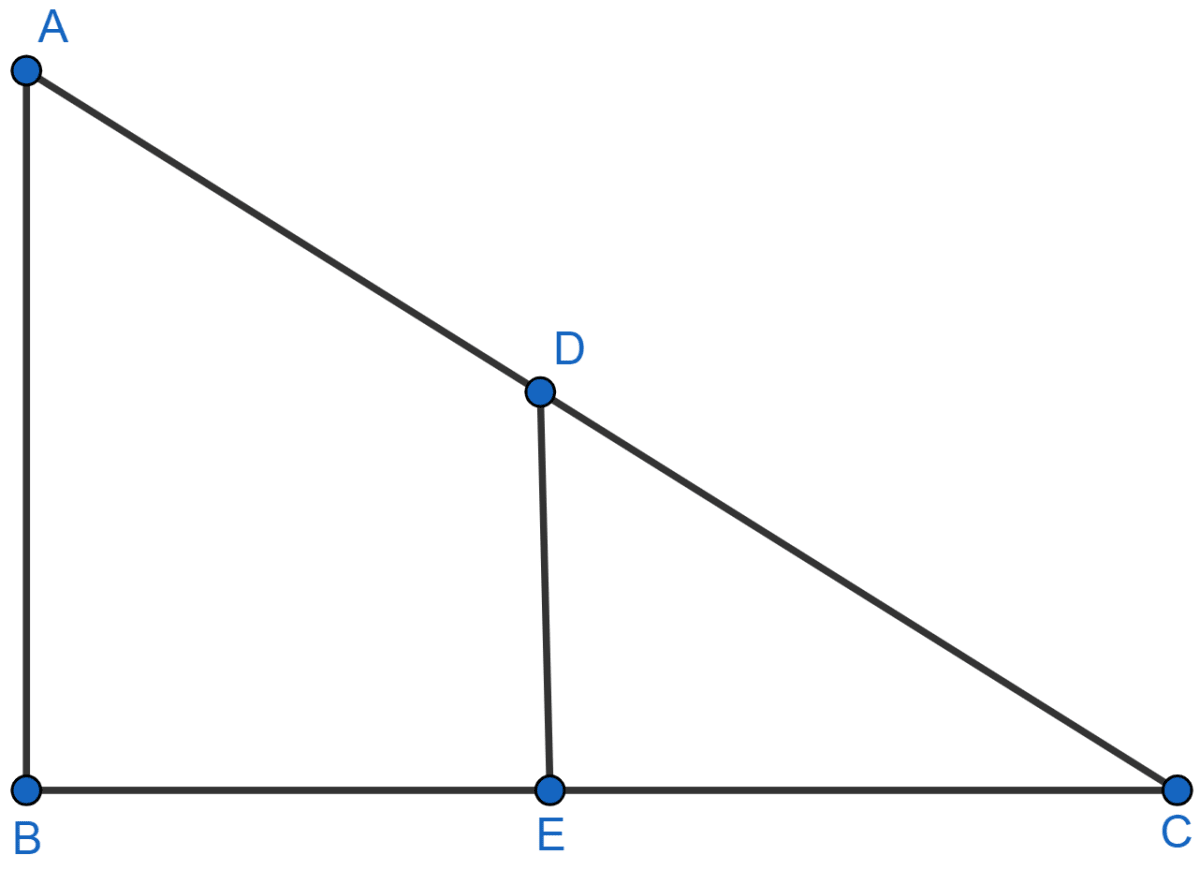
(i) Prove that △ABC ~ △DEC.
(ii) If AB = 6 cm, DE = 4 cm and AC = 15 cm, calculate CD.
(iii) Find the ratio of the area of △ABC : area of △DEC.
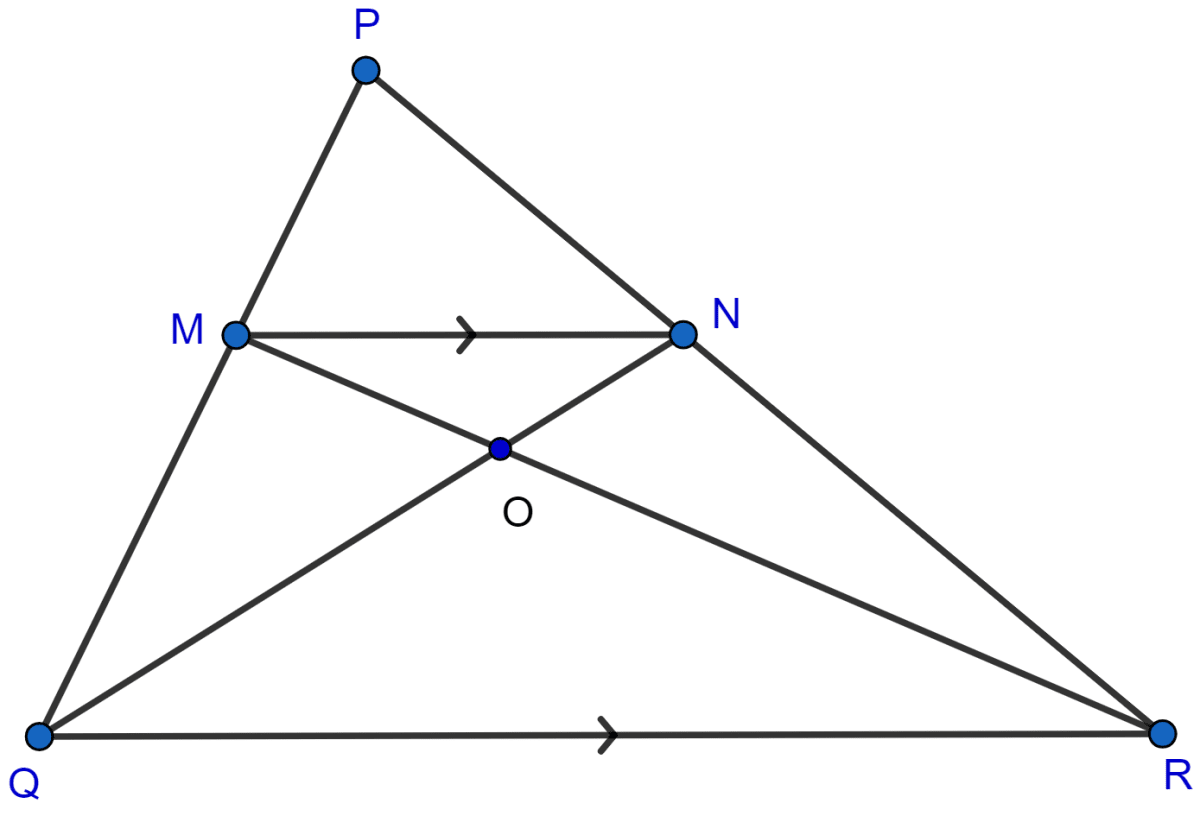
In △PQR, MN is parallel to QR and
(i) Find .
(ii) Prove that △OMN and △ORQ are similar.
(iii) Find area of △OMN : area of △ORQ.
In △ABC, AP : PB = 2 : 3. PO is parallel to BC and is extended to Q so that CQ is parallel to BA. Find :
(i) area △APO : area △ABC
(ii) area △APO : area △CQO.
