Mathematics
In the figure (ii) given below, O is the center of the circle. If ∠OAD = 50°, find the values of x and y.

Circles
36 Likes
Answer
From figure,
ABCD is a cyclic quadrilateral as all vertices lie on the circumference of the circle.
Sum of opposite angles of cyclic quadrilateral = 180°
⇒ ∠BCD + ∠BAD = 180°
⇒ x + 50° = 180°
⇒ x = 180° - 50°
⇒ x = 130°.
OA = OD = radius of the circle.
So, in △ODA,
∠ODA = ∠OAD = 50°.
In triangle exterior angle is equal to the sum of the opposite two interior angle.
y = ∠ODA + ∠OAD = 50° + 50° = 100°.
Hence, the value of x = 130° and y = 100°.
Answered By
19 Likes
Related Questions
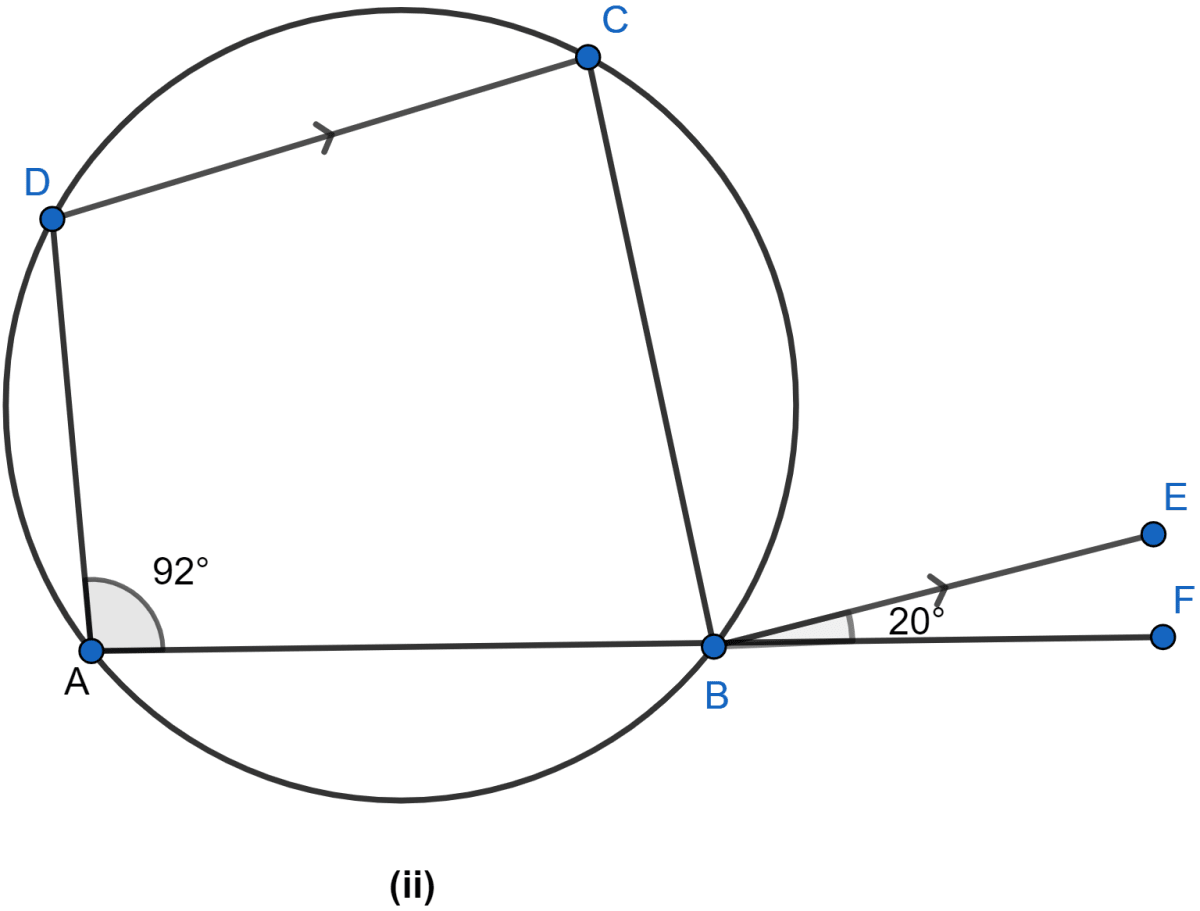
In figure (ii) given below, ABF is a straight line and BE || DC. If ∠DAB = 92° and ∠EBF = 20°, find
(i) ∠BCD
(ii) ∠ADC
In the figure (i) given below, PQRS is a cyclic quadrilateral in which PQ = QR and RS is produced to T. If ∠QPR = 52°, calculate ∠PST.

In the figure (i) given below, O is the center of the circle. If ∠COD = 40° and ∠CBE = 100°, then find :
(i) ∠ADC
(ii) ∠DAC
(iii) ∠ODA
(iv) ∠OCA

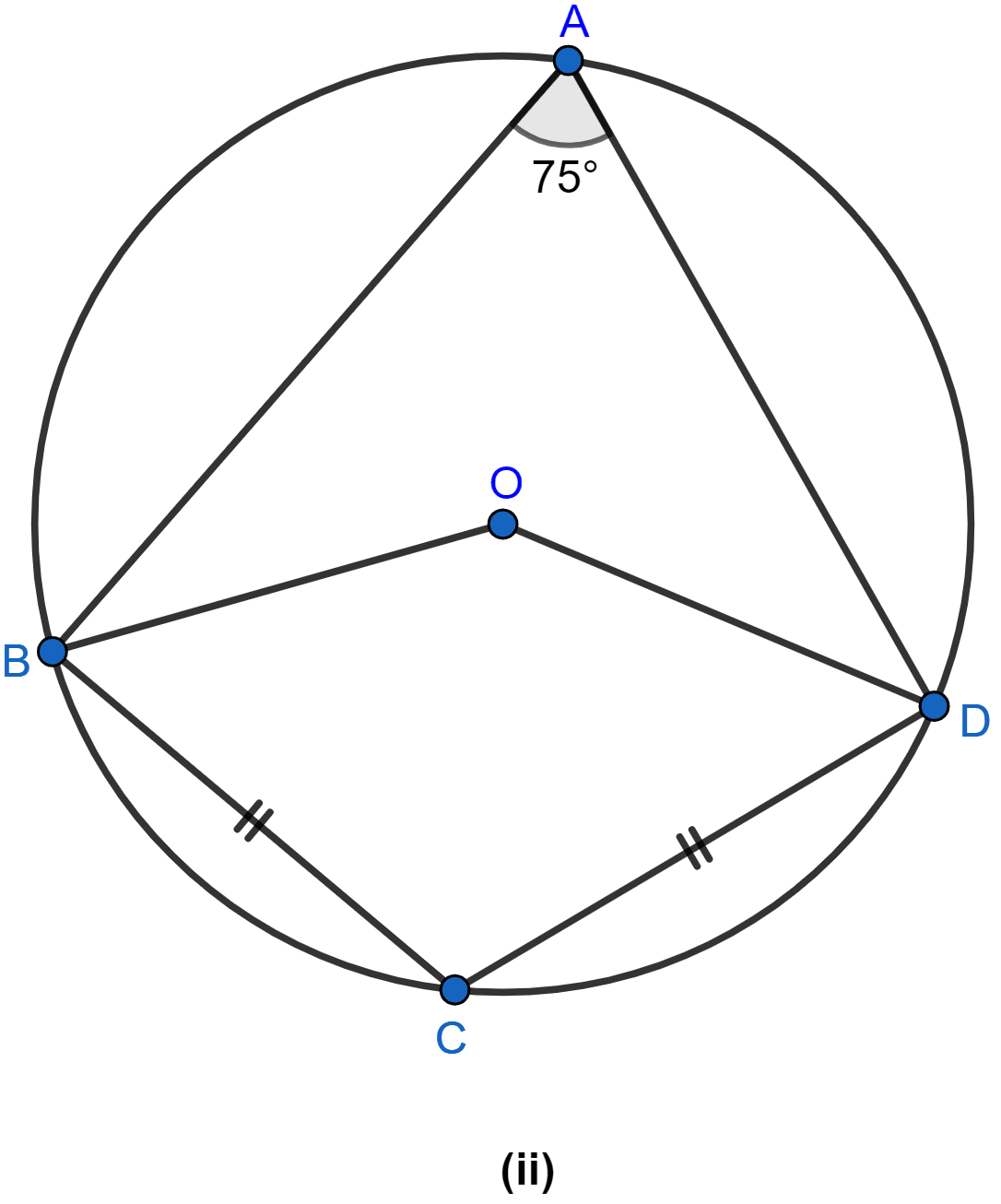
In the figure (ii) given below, O is the center of the circle. If ∠BAD = 75° and BC = CD, find:
(i) ∠BOD
(ii) ∠BCD
(iii) ∠BOC
(iv) ∠OBD