Mathematics
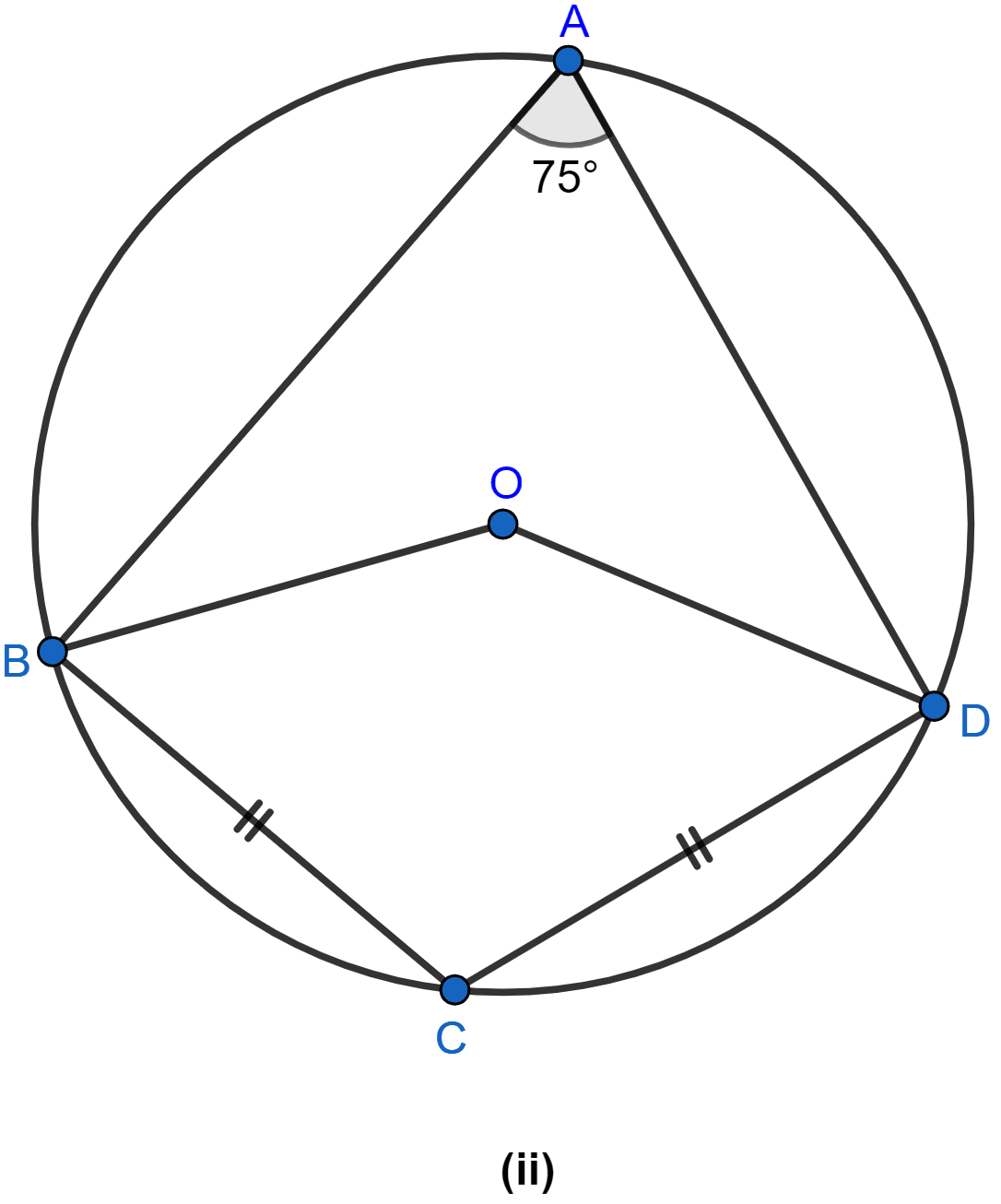
In the figure (ii) given below, O is the center of the circle. If ∠BAD = 75° and BC = CD, find:
(i) ∠BOD
(ii) ∠BCD
(iii) ∠BOC
(iv) ∠OBD
Circles
43 Likes
Answer
Join OC and BD as shown in the figure below:
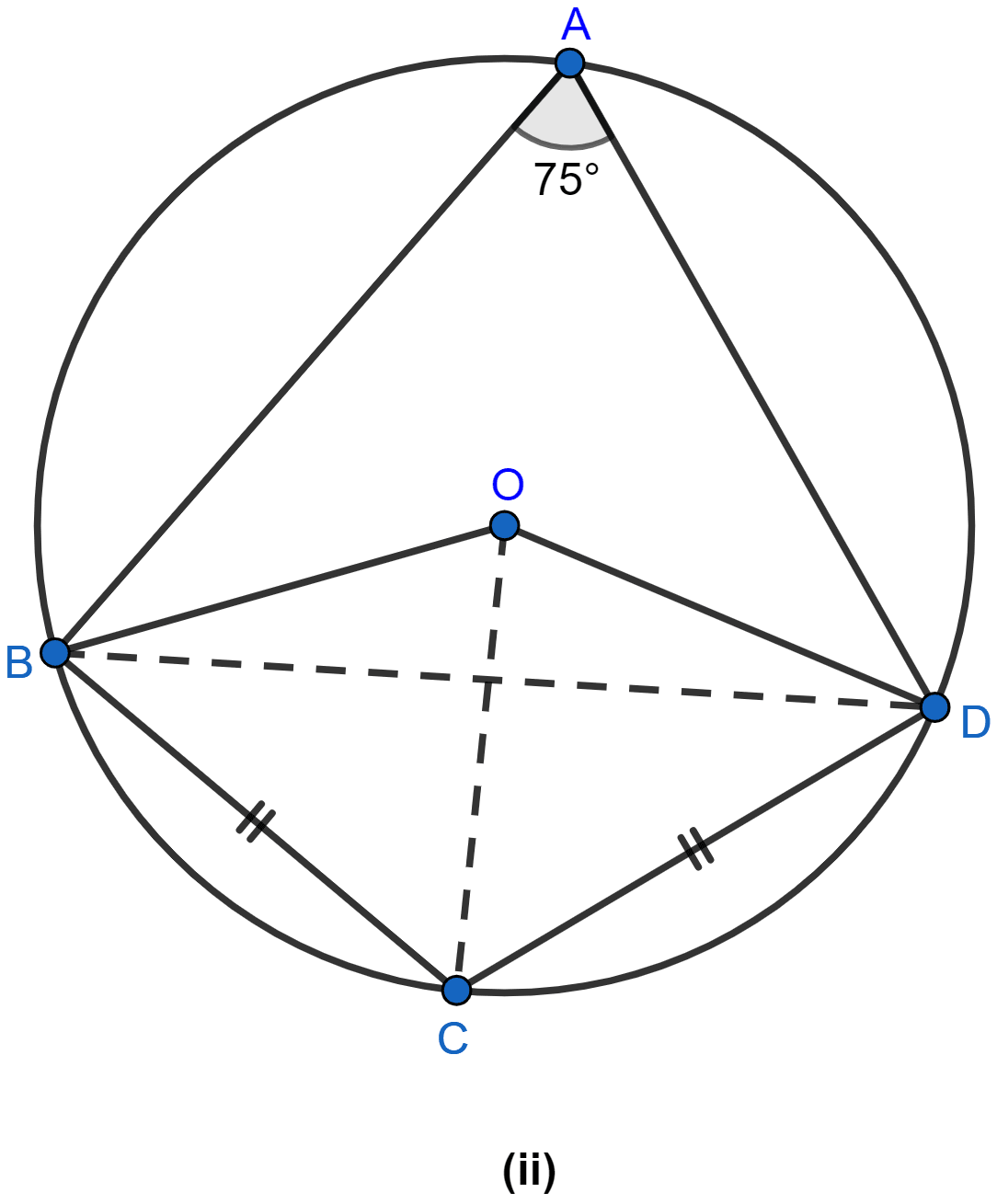
(i) ∠BOD = 2 × ∠BAD (∵ angle subtended by an arc at center is double the angle subtended at any point on the remaining part of the circle.)
∠BOD = 2 × 75° = 150°.
Hence, the value of ∠BOD = 150°.
(ii) ABCD is a cyclic quadrilateral as all of its vertices lie on the circumference of the circle.
We know that sum of opposite angles of a cyclic quadrilateral = 180°.
⇒ ∠BCD + ∠BAD = 180°
⇒ ∠BCD + 75° = 180°
⇒ ∠BCD = 180° - 75°
⇒ ∠BCD = 105°.
Hence, the value of ∠BCD = 105°.
(iii) Join OC.
As equal chords of a circle subtend equal angles at the center and chord BC = chord CD, so ∠BOC = ∠COD.
∠BOC = ∠BOD = = 75°.
Hence, the value of ∠BOC = 75°.
(iv) Join BD.
Since, OB = OD
∴ ∠OBD = ∠ODB = x
Since sum of angles of triangle = 180°
In △OBD
⇒ ∠BOD + ∠OBD + ∠ODB = 180°
⇒ 150° + x + x = 180°
⇒ 150° + 2x = 180°
⇒ 2x = 180° - 150°
⇒ 2x = 30°
⇒ x = 15°.
Hence, the value of ∠OBD = 15°.
Answered By
23 Likes
Related Questions
In the figure (ii) given below, O is the center of the circle. If ∠OAD = 50°, find the values of x and y.

In the figure (i) given below, O is the center of the circle. If ∠COD = 40° and ∠CBE = 100°, then find :
(i) ∠ADC
(ii) ∠DAC
(iii) ∠ODA
(iv) ∠OCA

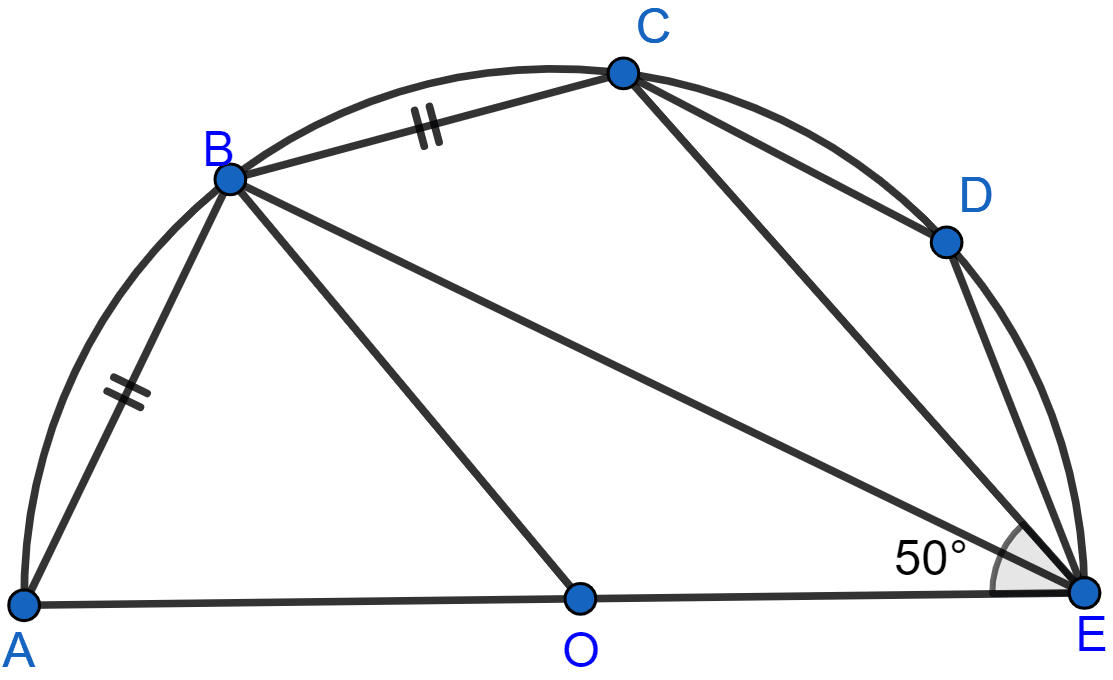
In the adjoining figure, O is the center and AOE is the diameter of the semicircle ABCDE. If AB = BC and ∠AEB = 50°, find :
(i) ∠CBE
(ii) ∠CDE
(iii) ∠AOB.
Prove that OB is parallel to EC.
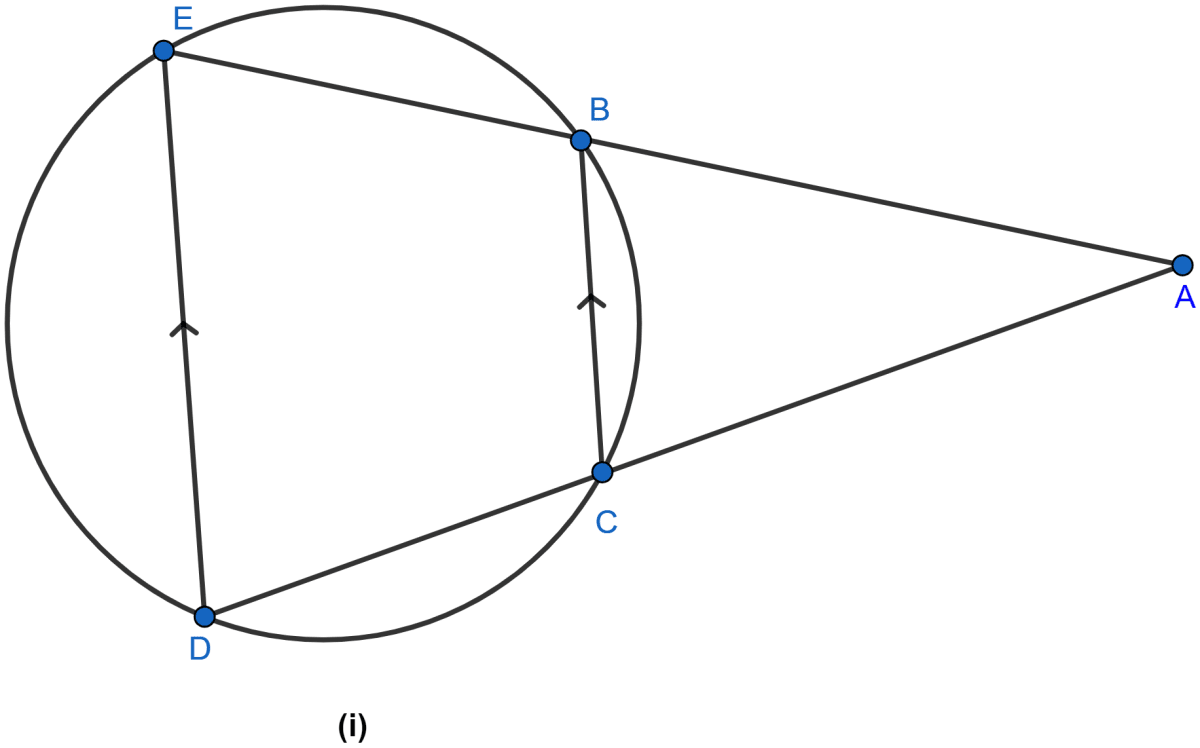
In the figure (i) given below, ED and BC are two parallel chords of the circle and ABE, ACD are two st. lines. Prove that AED is an isosceles triangle.