Mathematics
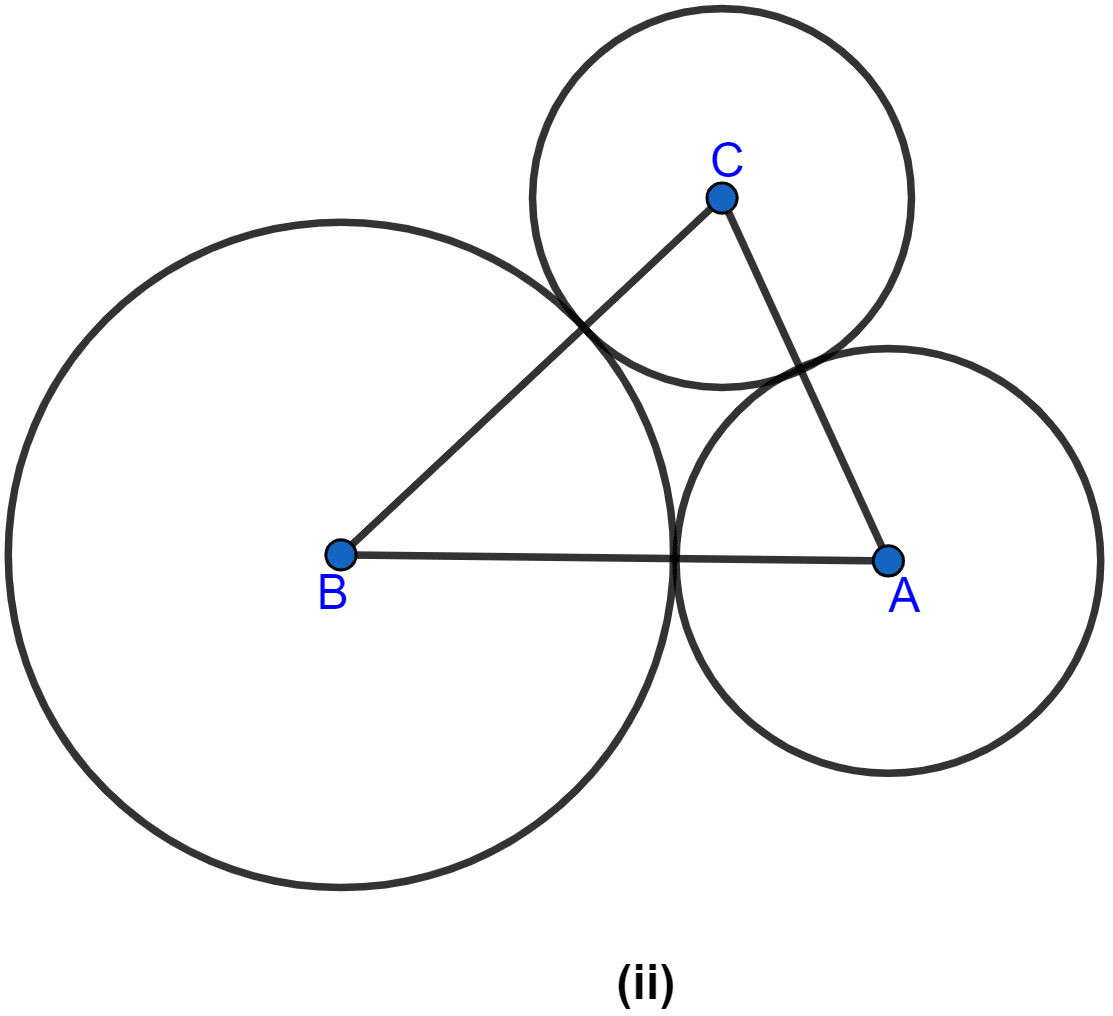
In the figure (ii) given below, ABC is a triangle with AB = 10 cm, BC = 8 cm and AC = 6 cm (not drawn to scale). Three circles are drawn touching each other with vertices A, B and C as their centres. Find the radii of the three circles.
Answer
Given, AB = 10 cm, BC = 8 cm, AC = 6 cm
Let the radius of the circles with centre A, B and C be x cm, y cm and z cm.
From figure,
AB = 10 cm.
⇒ x + y = 10 cm ….(i)
BC = 8 cm.
⇒ y + z = 8 cm ….(ii)
AC = 6 cm.
⇒ x + z = 6 cm …..(iii)
Adding eqn. (i), (ii) and (iii) we get,
⇒ x + y + y + z + x + z = (10 + 8 + 6) cm
⇒ 2x + 2y + 2z = 24 cm
⇒ 2(x + y + z) = 24 cm
⇒ x + y + z = 12 cm …..(iv)
Now, (iv) - (i) we get,
⇒ x + y + z - (x + y) = (12 - 10) cm
⇒ x + y + z - x - y = 2 cm
⇒ z = 2 cm.
Also, by (iv) - (ii) we get,
⇒ x + y + z - (y + z) = (12 - 8) cm
⇒ x + y + z - y - z = 4 cm
⇒ x = 4 cm
Also, by (iv) - (iii) we get,
⇒ x + y + z - (x + z) = (12 - 6) cm
⇒ x + y + z - x - z = 6 cm
⇒ y = 6 cm.
Hence, the radius of the circle with centre A, B and C are 4 cm, 6 cm and 2 cm.
Related Questions
Three circles of radii 2 cm, 3 cm and 4 cm touch each other externally. Find the perimeter of the triangle obtained on joining the centres of these circles.
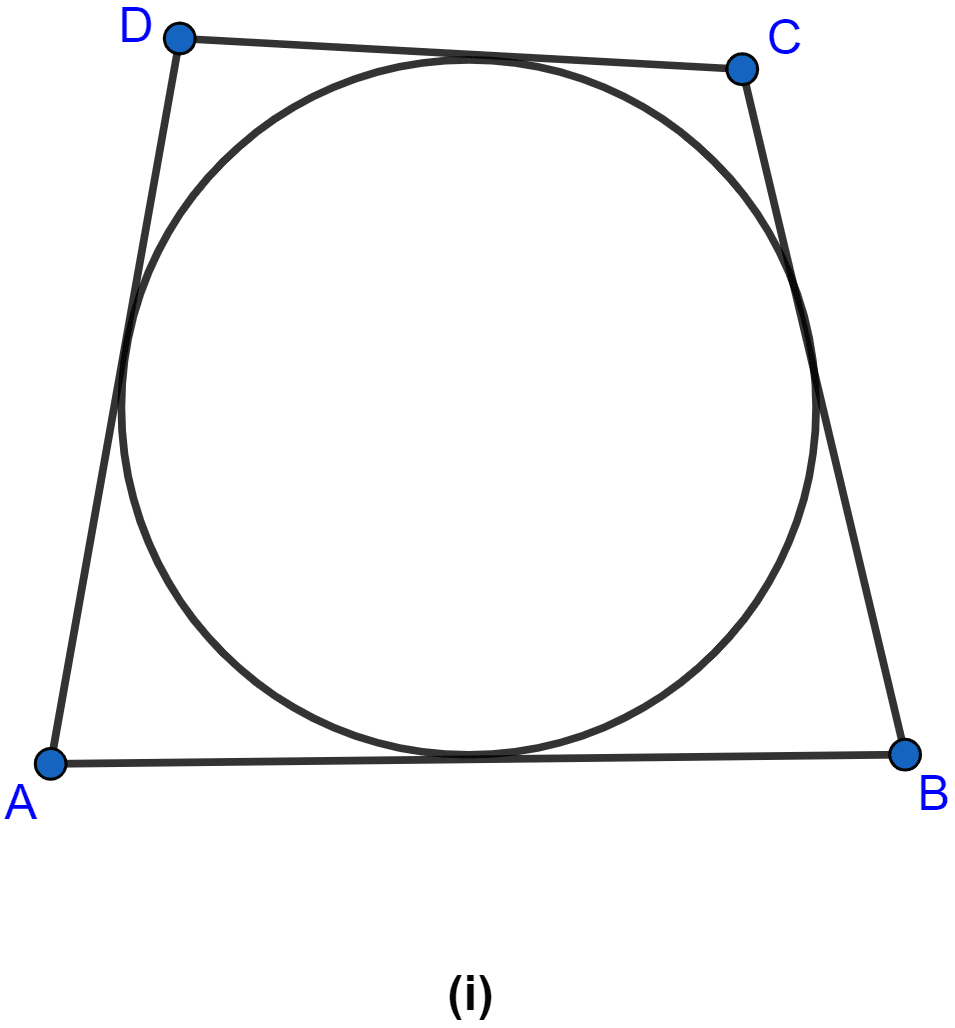
In the figure (i) given below, the sides of the quadrilateral touch the circle. Prove that AB + CD = BC + DA.
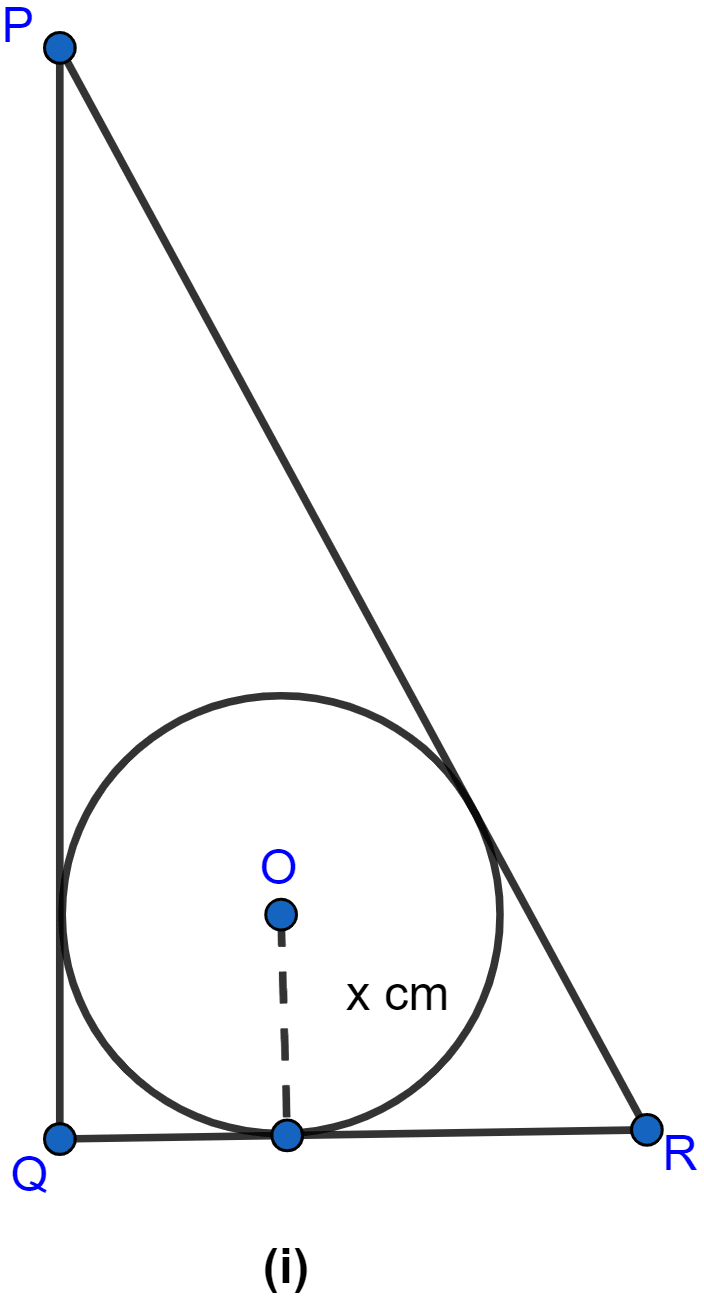
In the figure (i) given below, PQ = 24 cm, QR = 7 cm and ∠PQR = 90°. Find the radius of the inscribed circle of △PQR.
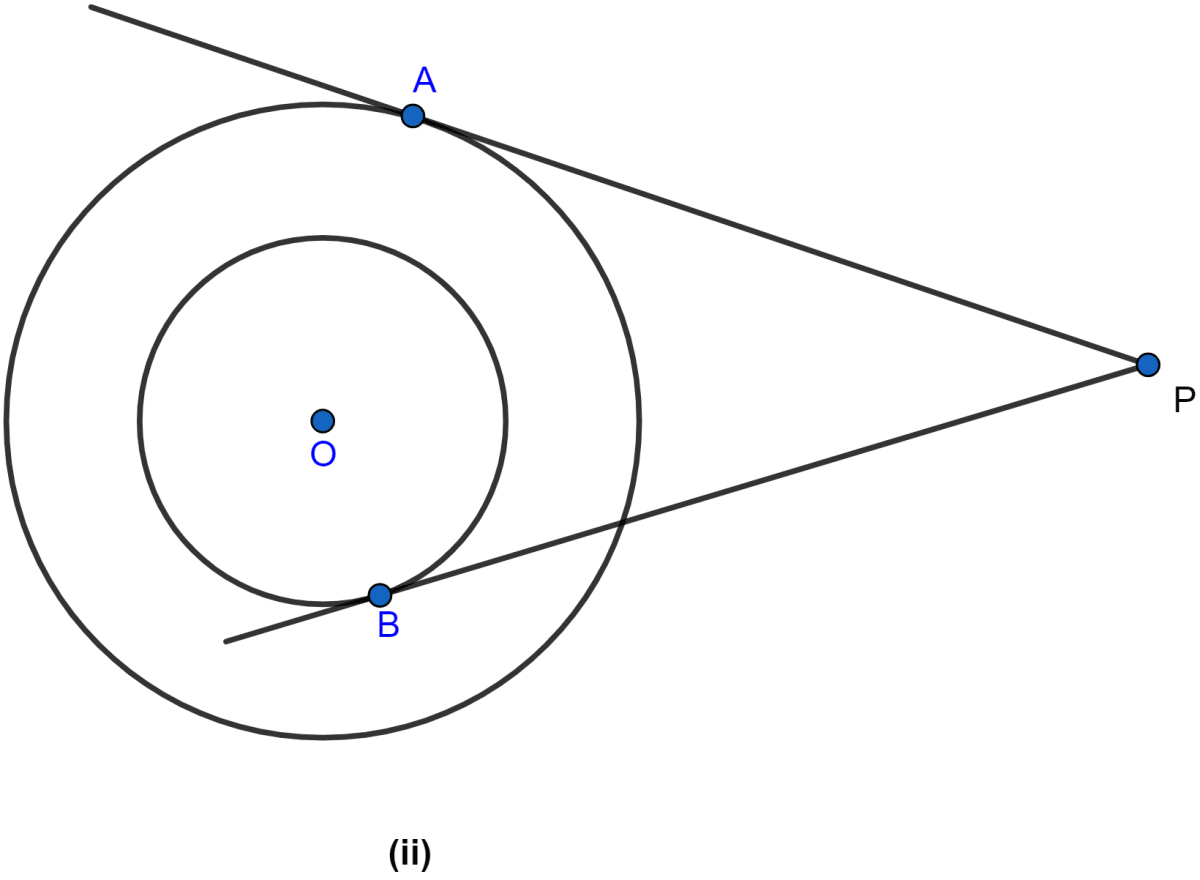
In the figure (ii) given below, two concentric circles with centre O are of radii 5 cm and 3 cm. From an external point P, tangents PA and PB are drawn to these circles. If AP = 12 cm, find BP.