Mathematics
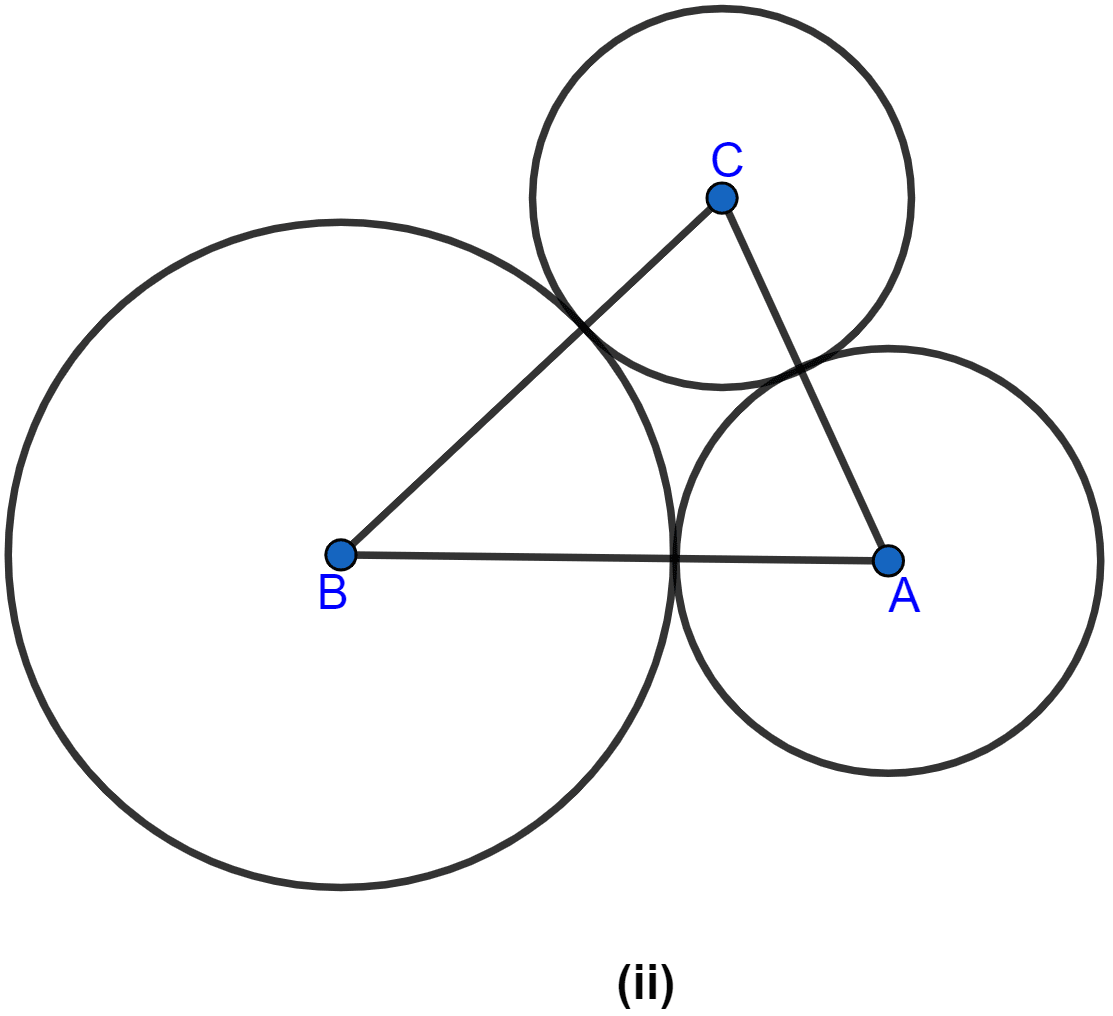
Three circles of radii 2 cm, 3 cm and 4 cm touch each other externally. Find the perimeter of the triangle obtained on joining the centres of these circles.
Circles
30 Likes
Answer
Three circles with centres A, B and C touch each other externally and the radii of these circles are 2 cm, 3 cm and 4 cm respectively.
From figure,

By joining the centres of circles, triangle ABC is formed in which,
AB = 2 + 3 = 5 cm
BC = 3 + 4 = 7 cm
CA = 4 + 2 = 6 cm.
Therefore, perimeter of the triangle ABC = AB + BC + CA = 5 + 7 + 6 = 18 cm.
Hence, the perimeter of triangle ABC = 18 cm.
Answered By
21 Likes
Related Questions
If a, b, c are the sides of a right angled triangle where c is the hypotenuse, prove that the radius r of the circle which touches the sides of the triangle is given by r = .
In the given figure, PB is a tangent to a circle with centre O at B. AB is a chord of length 24 cm at a distance of 5 cm from the centre. If the length of the tangent is 20 cm, find the length of OP.

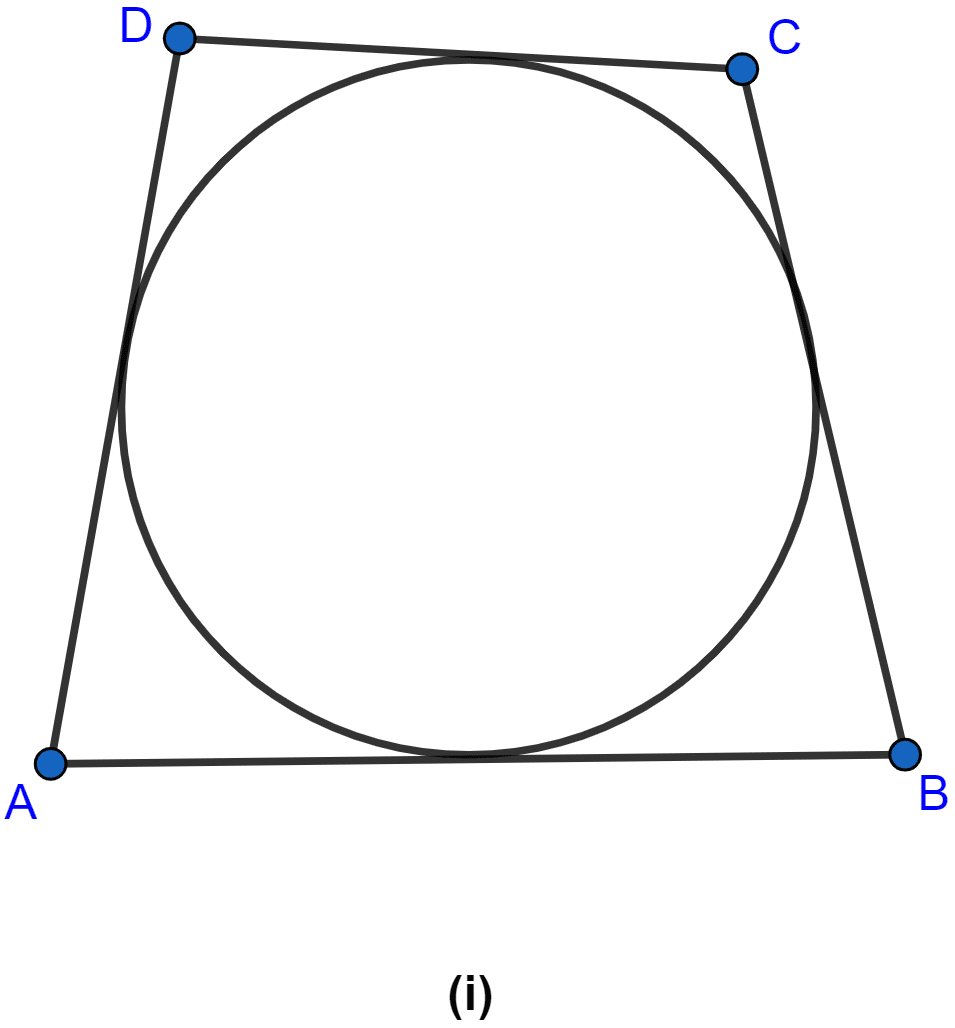
In the figure (i) given below, the sides of the quadrilateral touch the circle. Prove that AB + CD = BC + DA.
In the figure (ii) given below, ABC is a triangle with AB = 10 cm, BC = 8 cm and AC = 6 cm (not drawn to scale). Three circles are drawn touching each other with vertices A, B and C as their centres. Find the radii of the three circles.