Mathematics
In the figure (i) given below, O is the centre of the circle and SP is a tangent. If ∠SRT = 65°, find the values of x, y and z.

Answer
From figure,
In △SRT,
SR ⊥ ST (∵ tangent is perpendicular to radius from that point.)
so, ∠TSR = 90°
Since, sum of angles in a triangle = 180°
⇒ ∠TSR + ∠SRT + ∠STR = 180°
⇒ 90° + 65° + x = 180°
⇒ x + 155° = 180°
⇒ x = 25°.
SQ subtends ∠SOQ at the centre and ∠STQ on point D.
∴ ∠SOQ = 2∠STQ (∵ angle subtended at centre by an arc is double the angle subtended at remaining part of circle.)
y = 2x = 2 × 25° = 50°.
In △OSP,
Since, sum of angles in a triangle = 180
⇒ ∠OSP + ∠SOP + ∠SPO = 180°
⇒ 90° + y + z = 180°
⇒ 90° + 50° + z = 180°
⇒ z + 140° = 180°
⇒ z = 180° - 140° = 40°.
Hence, the value of x = 25°, y = 50° and z = 40°.
Related Questions
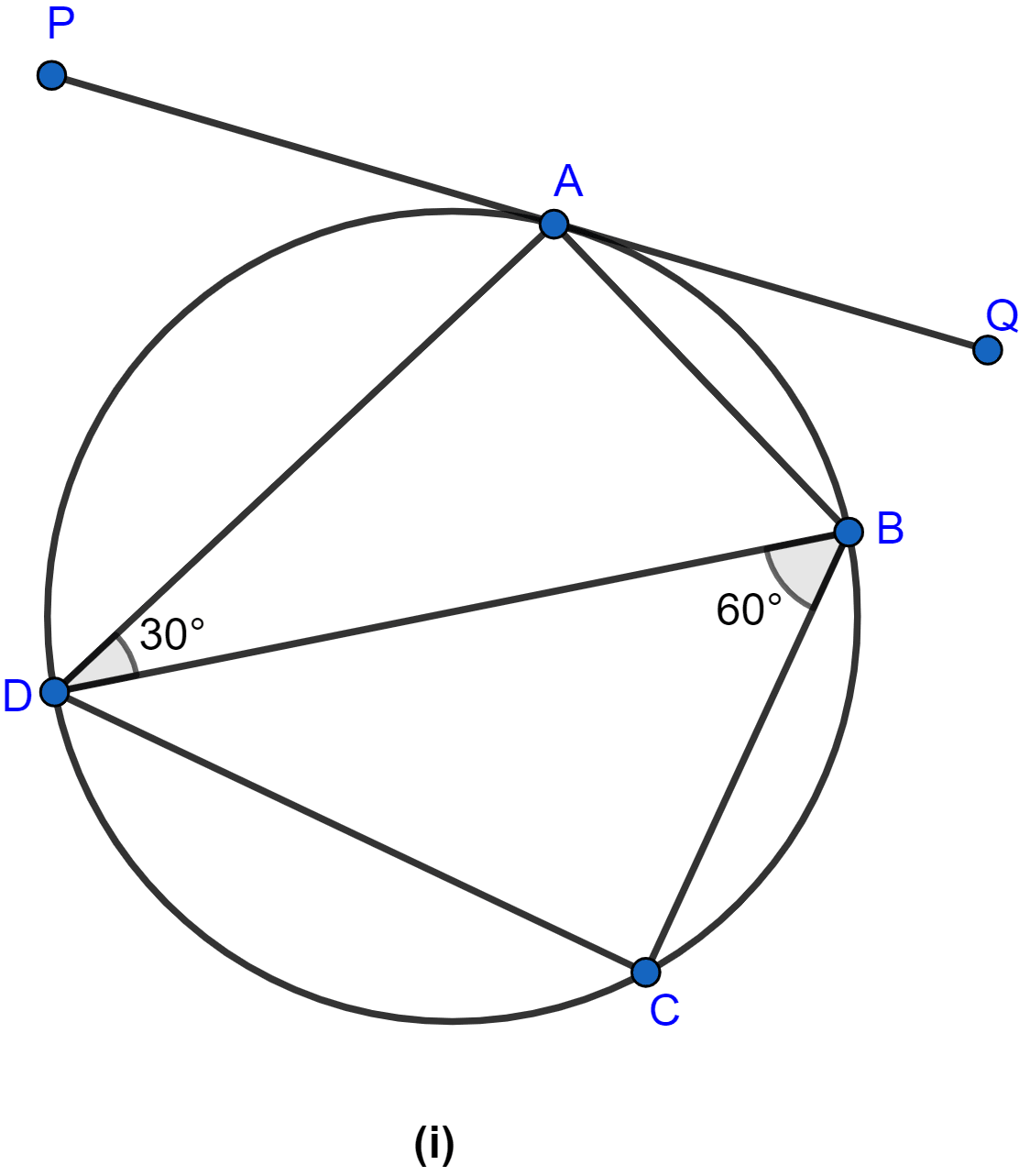
In the figure (i) given below, PQ is a tangent to the circle at A, DB is a diameter, ∠ADB = 30° and ∠CBD = 60°, calculate
(i) ∠QAB
(ii) ∠PAD
(iii) ∠CDB.
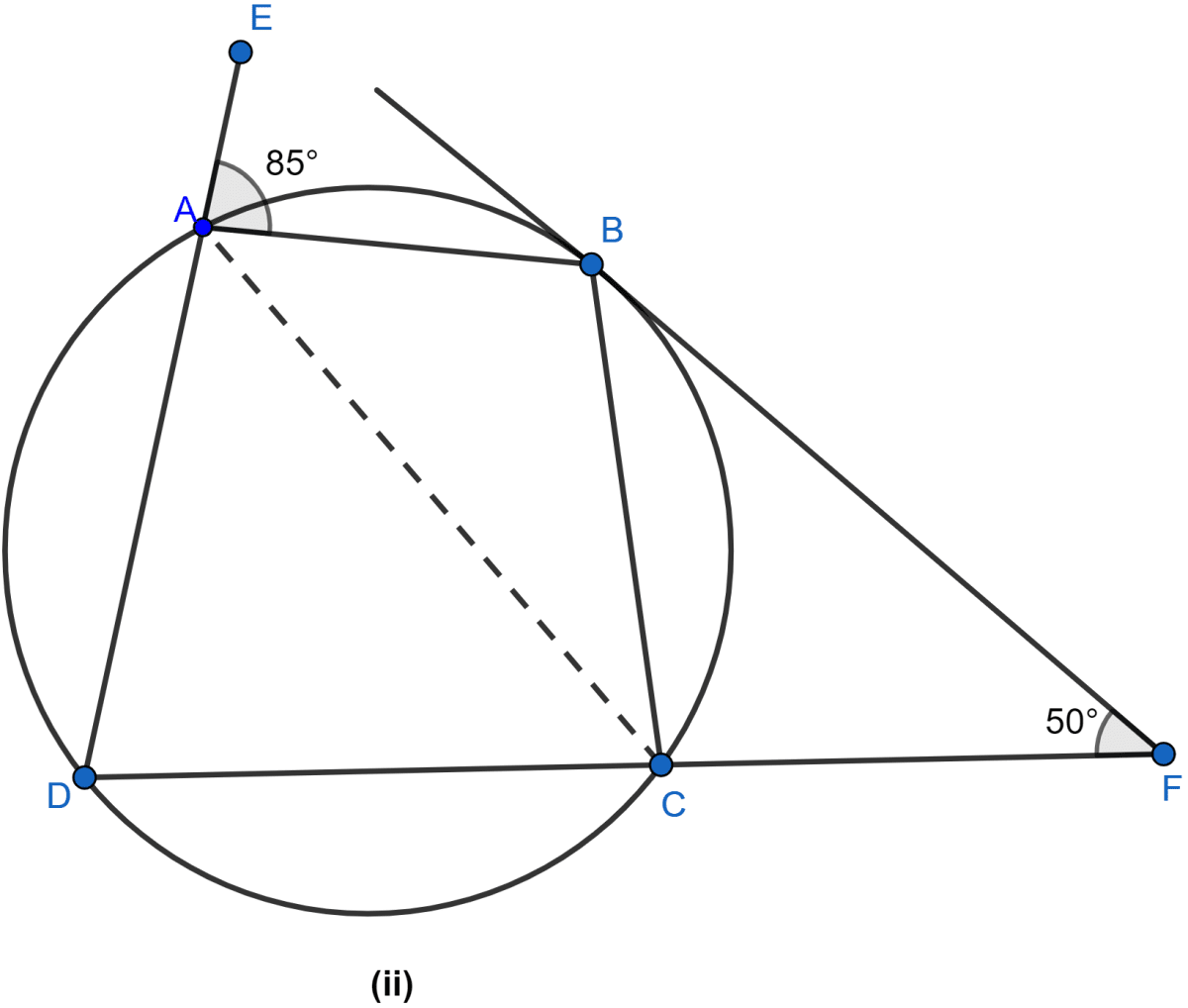
In the figure (ii) given below, ABCD is a cyclic quadrilateral. The tangent to the circle at B meets DC produced at F. If ∠EAB = 85° and ∠BFC = 50°, find ∠CAB.
In the figure (ii) given below, O is the centre of the circle. PS and PT are tangents and ∠SPT = 84°. Calculate the sizes of the angles TOS and TQS.
In the adjoining figure, O is the centre of the circle. Tangents to the circle at A and B meet at C. If ∠ACO = 30°, find
(i) ∠BCO
(ii) ∠AOB
(iii) ∠APB
