Mathematics
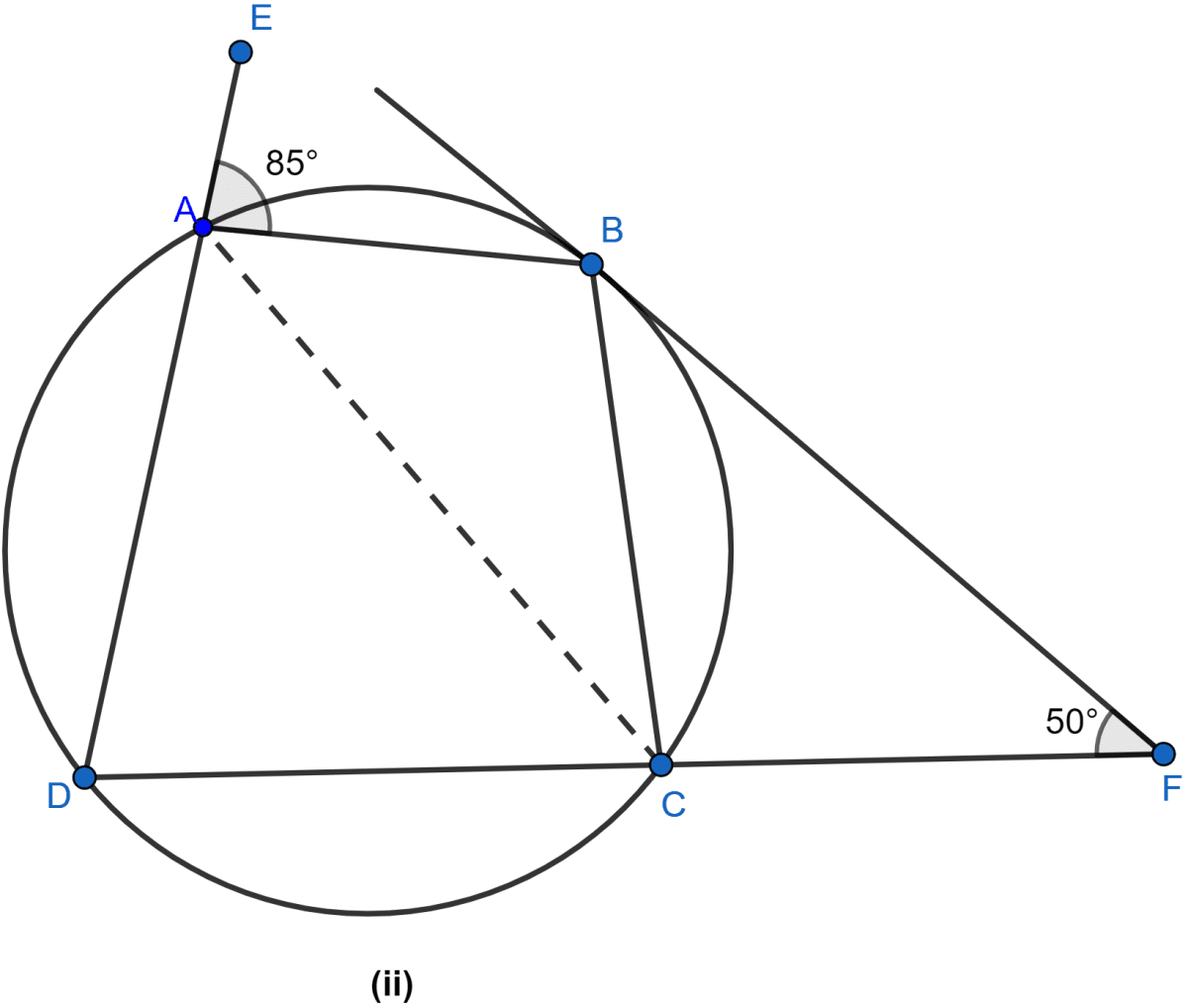
In the figure (ii) given below, ABCD is a cyclic quadrilateral. The tangent to the circle at B meets DC produced at F. If ∠EAB = 85° and ∠BFC = 50°, find ∠CAB.
Circles
60 Likes
Answer
ABCD is a cyclic quadrilateral.
In cyclic quadrilateral, the exterior angle = opposite interior angle.
∴ ∠BCD = ∠EAB = 85°
From figure,
⇒ ∠BCD + ∠BCF = 180° (∵ both are linear pair)
⇒ ∠BCF + 85° = 180°
⇒ ∠BCF = 95°.
Now in △BCF,
Since, sum of angles in a triangle is 180°.
⇒ ∠BCF + ∠BFC + ∠CBF = 180°
⇒ 95° + 50° + ∠CBF = 180°
⇒ ∠CBF + 145° = 180°
⇒ ∠CBF = 35°.
We know, BF is a tangent and BC is a chord.
∴ ∠CAB = ∠CBF = 35° (∵ angles in alternate segment are equal.)
⇒ ∠CAB = 35°.
Hence, the value of ∠CAB = 35°.
Answered By
40 Likes
Related Questions
In the figure (i) given below, PQ is a tangent to the circle at A, DB is a diameter, ∠ADB = 30° and ∠CBD = 60°, calculate
(i) ∠QAB
(ii) ∠PAD
(iii) ∠CDB.
In the figure (ii) given below, O is the centre of the circle. PS and PT are tangents and ∠SPT = 84°. Calculate the sizes of the angles TOS and TQS.
In the given figure, tangents PQ and PR are drawn from an external point P to a circle such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQ. Find ∠RQS.
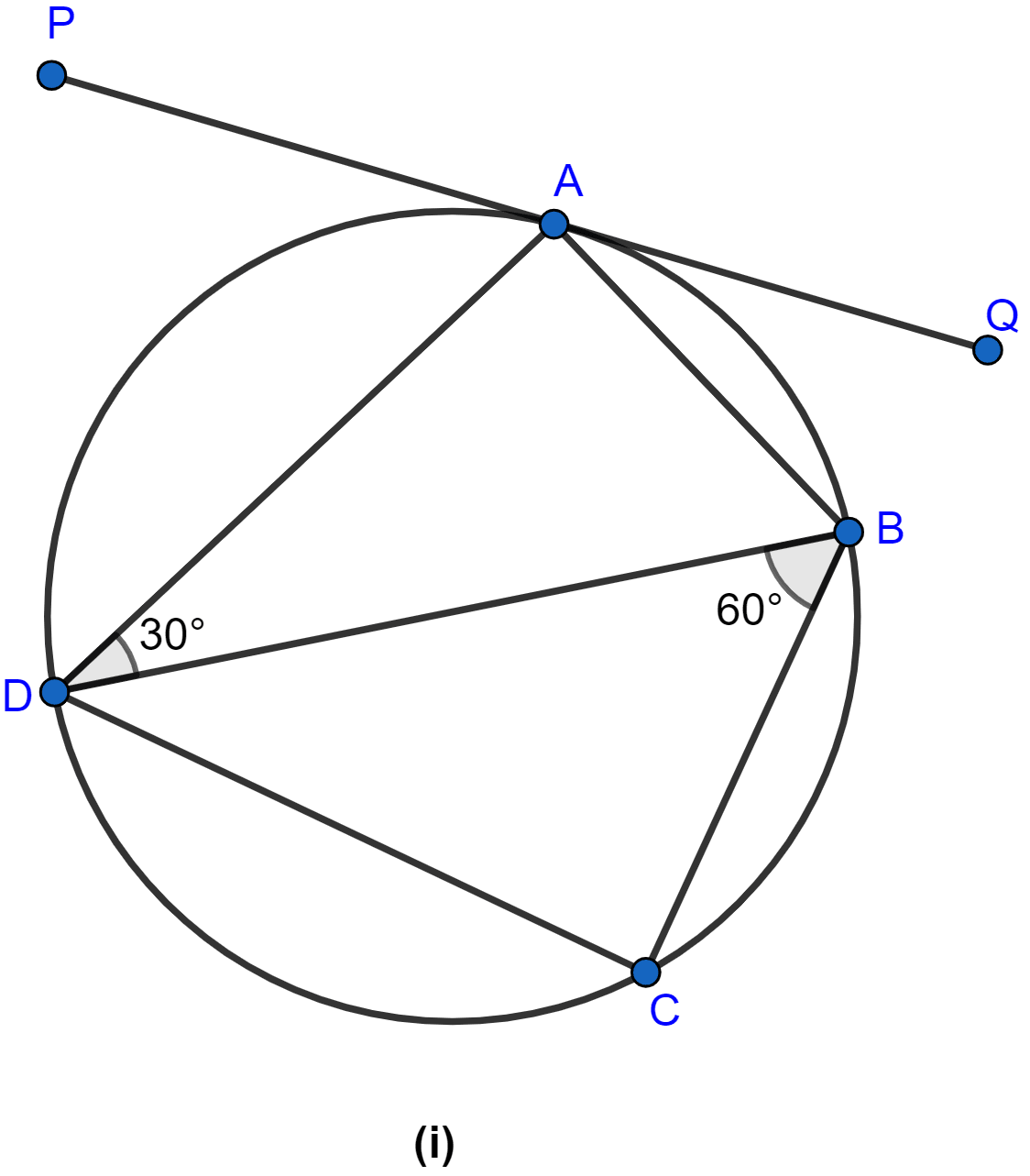
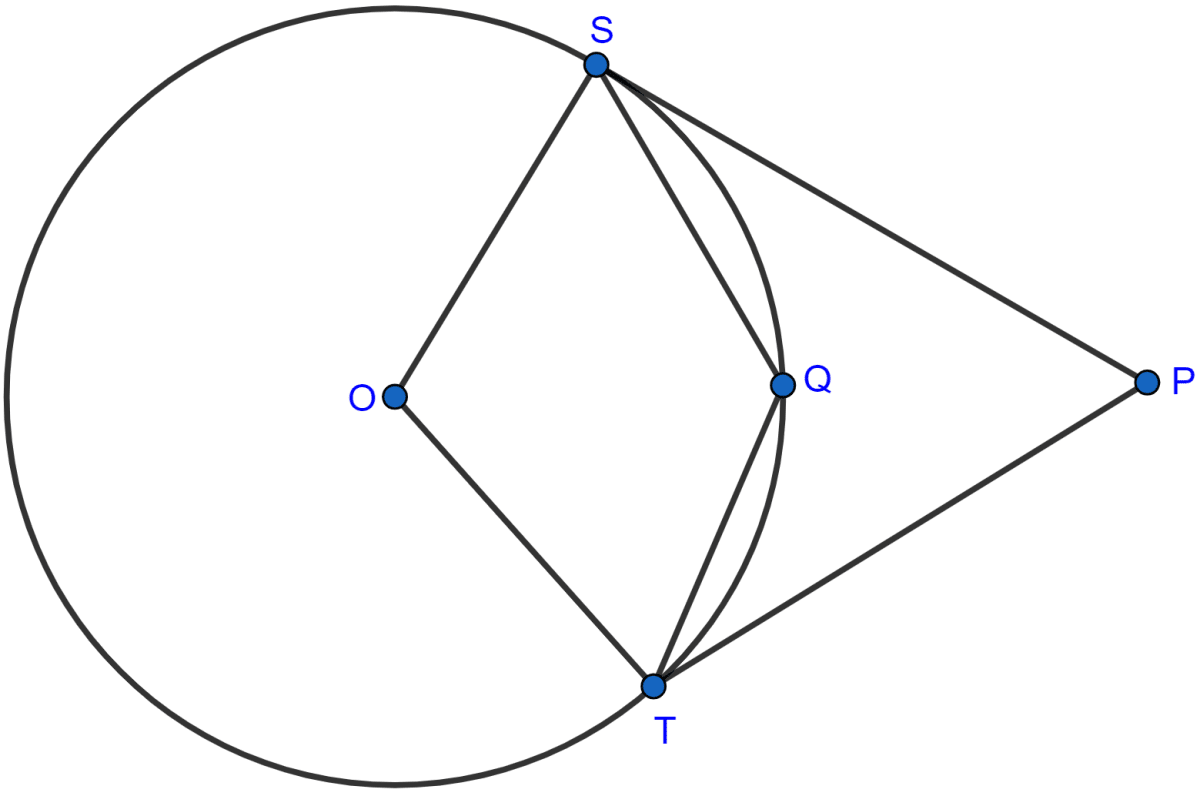
In the figure (i) given below, O is the centre of the circle and SP is a tangent. If ∠SRT = 65°, find the values of x, y and z.
