Mathematics
In the figure given below, D and E are mid-points of AB, BC respectively and DF || BC. Prove that DBEF is a parallelogram. Calculate AC if AF = 2.6 cm.
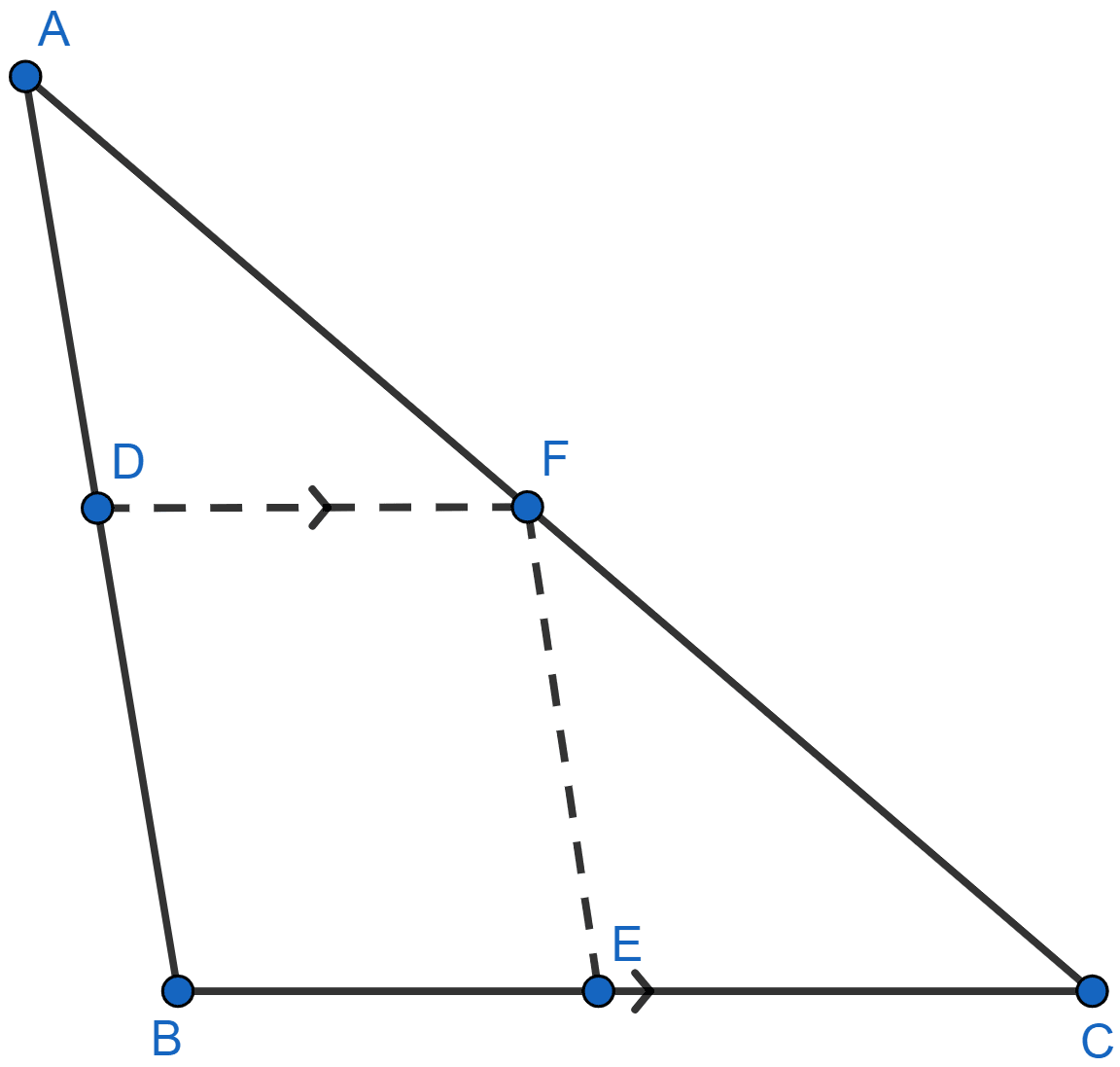
Answer
In △ABC,
D is the midpoint of AB and DF || BC
∴ F is the midpoint of AC (By converse of mid-point theorem)
F and E are midpoints of AC and BC respectively
∴ EF || AB ⇒ EF || DB …..(1)
From figure,
⇒ DF || BE ……(2)
Using 1 and 2,
⇒ EF || DB and DF || BE
Hence, proved that DBEF is a parallelogram.
F is the midpoint of AC we get,
AC = 2 × AF = 2 × 2.6 = 5.2 cm
Hence, AC = 5.2 cm
Related Questions
In the figure given below, D, E and F are mid-points of the sides BC, CA and AB respectively of △ ABC. If AB = 6 cm, BC = 4.8 cm and CA = 5.6 cm, find the perimeter of
(i) the trapezium of FBCE
(ii) the triangle DEF.
Prove that four triangles formed by joining in pairs, the mid-points of the sides of a triangle are congruent to each other.
If D, E and F are mid-points of the sides AB, BC and CA respectively of an isosceles triangle, ABC, prove that △DEF is also isosceles.
In the figure given below, D and E are mid-points of the sides AB and AC respectively. If BC = 5.6 cm and ∠B = 72°, compute
(i) DE
(ii) ∠ADE
