Mathematics
In the figure, AB is the chord of a circle with centre O and DOC is a line segment such that BC = DO. If ∠C = 20°, find angle AOD.

Answer
Join OB.
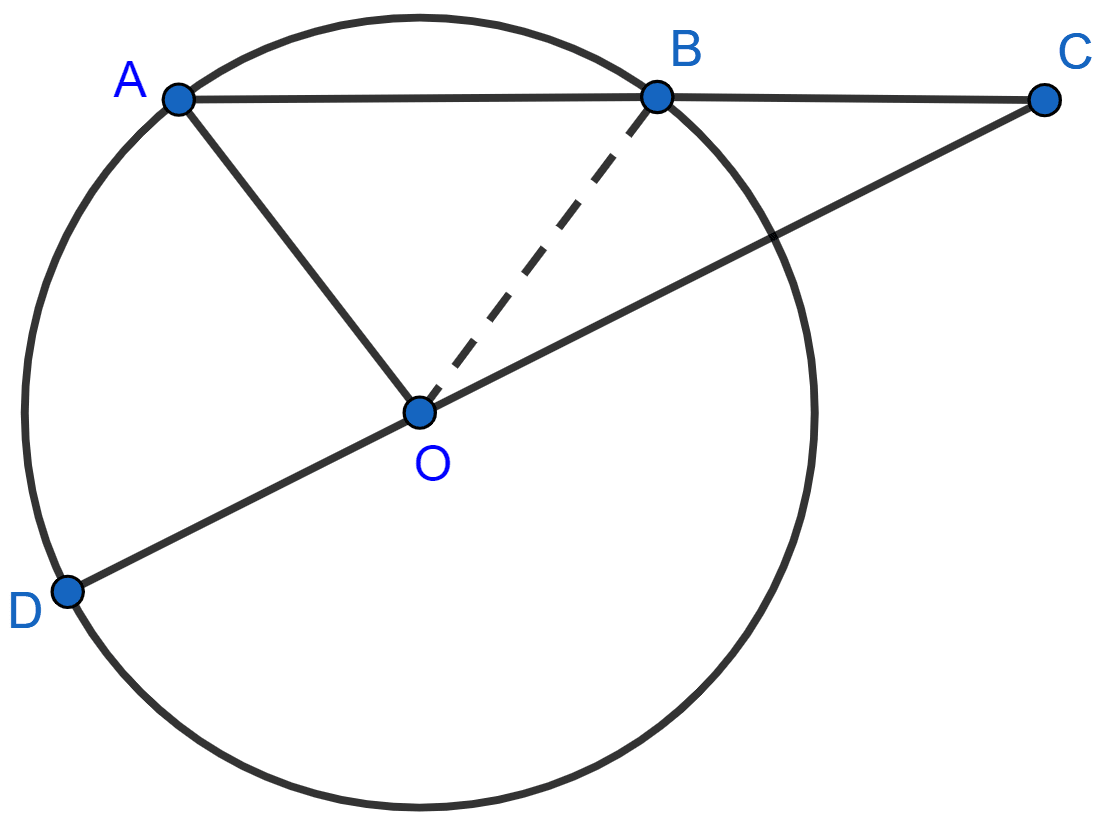
Given,
BC = OD = radius of circle
⇒ BC = OB.
As, angles opposite to equal sides are equal.
⇒ ∠BOC = ∠BCO = 20°.
An exterior angle is equal to the sum of two opposite interior angles.
∴ ∠ABO = ∠BCO + ∠BOC = 20° + 20° = 40° …………(1)
Now in ∆OAB,
OA = OB [Radii of the same circle]
As, angles opposite to equal sides are equal.
∠OAB = ∠ABO = 40° [from (1)]
By angle sum property of triangle,
⇒ ∠AOB + ∠OAB + ∠OBA = 180°
⇒ ∠AOB + 40° + 40° = 180°
⇒ ∠AOB + 80° = 180°
⇒ ∠AOB = 180° - 80°
⇒ ∠AOB = 100°
As DOC is a straight line,
⇒ ∠AOD + ∠AOB + ∠BOC = 180°
⇒ ∠AOD + 100° + 20° = 180°
⇒ ∠AOD = 180° - 120° = 60°.
Hence, ∠AOD = 60°.
Related Questions
Show that the circle drawn on any one of the equal sides of an isosceles triangle as diameter bisects the base.
P is the midpoint of an arc APB of a circle. Prove that the tangent drawn at P will be parallel to the chord AB.
In the given figure, ABCD is a cyclic quadrilateral, PQ is tangent to the circle at point C and BD is its diameter. If ∠DCQ = 40° and ∠ABD = 60°, find:
(i) ∠DBC
(ii) ∠BCP
(iii) ∠ADB
