Mathematics
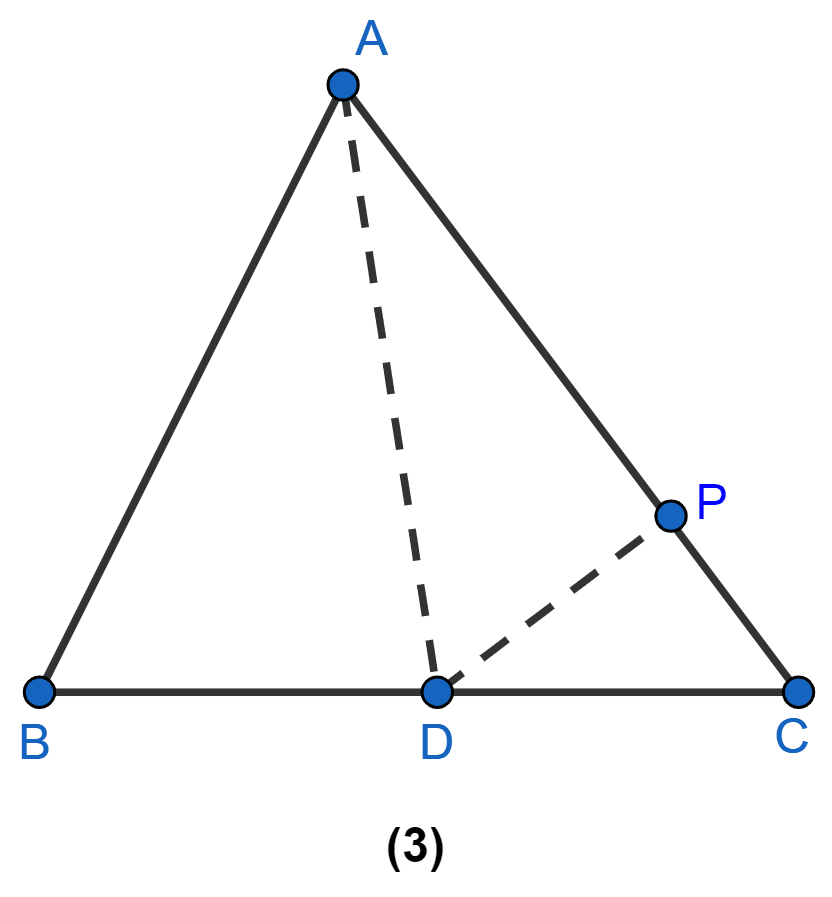
In the figure (3) given below, AD is a median of △ABC and P is a point in AC such that area of △ADP : area of △ABD = 2 : 3. Find
(i) AP : PC
(ii) area of △PDC : area of △ABC
Theorems on Area
15 Likes
Answer
(i) From figure,
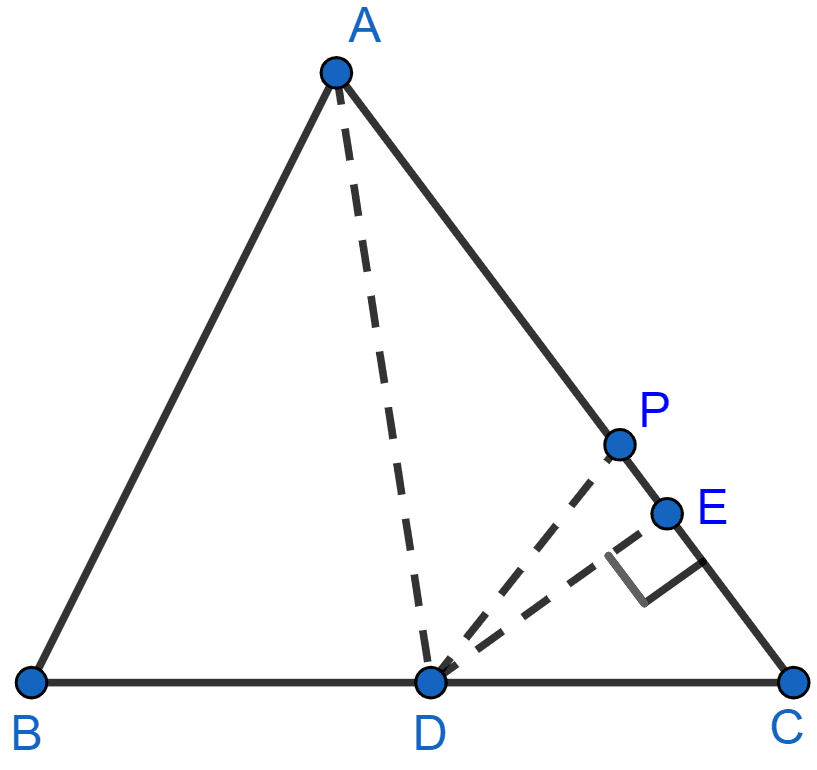
Let DE be altitude on base AC.
Median divides a triangle into two triangles of equal area.
AD is the median of ∆ABC,
Area of ∆ABD = Area of ∆ADC = Area of ∆ABC …….(1)
It is given that,
⇒ area of ∆ADP : area of ∆ABD = 2 : 3
⇒ area of ∆ADP : area of ∆ADC = 2 : 3
Let AP = 2x and AC = 3x.
From figure,
PC = AC - AP = 3x - 2x = x.
Hence, AP : PC = 2 : 1
(ii) We know that,
PC : AC = x : 3x = 1 : 3
So,
Since, AD is median of ∆ABC so,
area of ∆ADC = area of ∆ABC
Substituting above value in 1 we get,
Hence, proved that area of △PDC : area of △ABC = 1 : 6.
Answered By
9 Likes
Related Questions
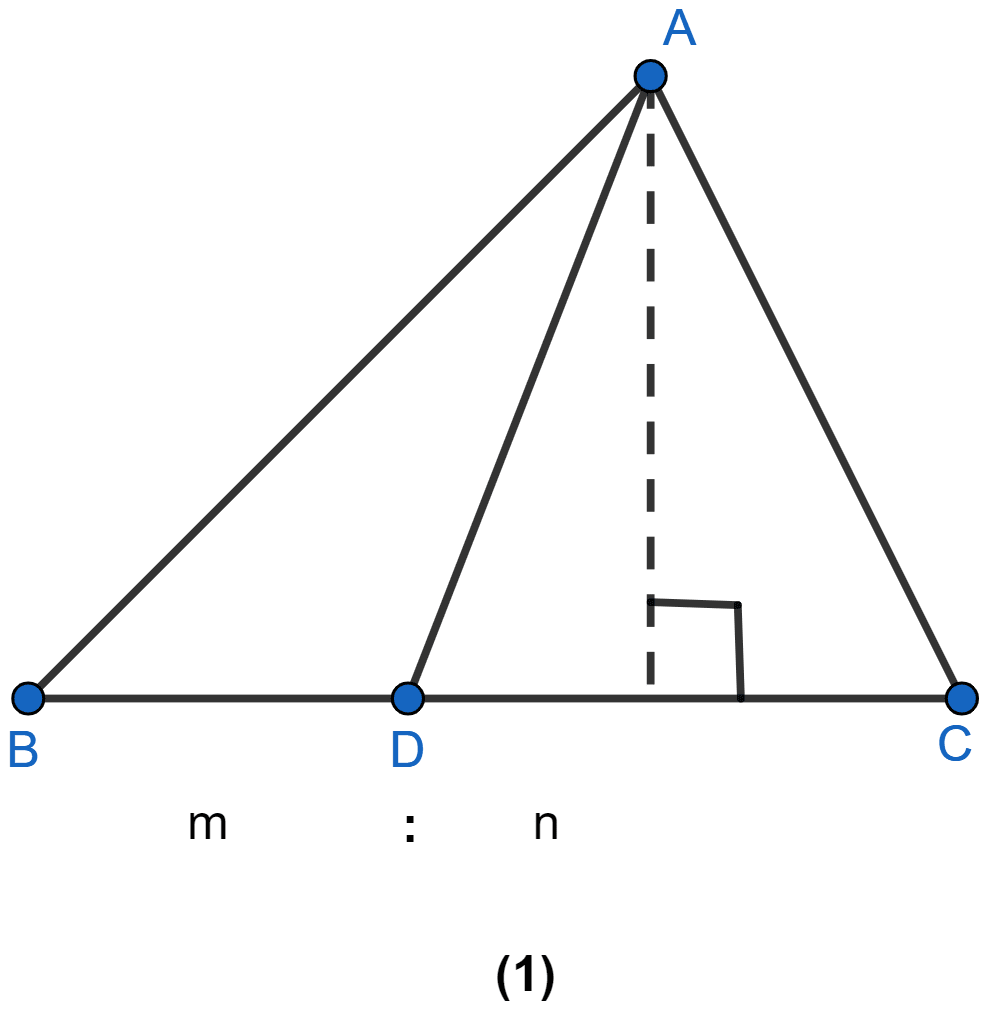
In figure (1) given below, point D divides the side BC of ∆ABC in the ratio m : n. Prove that area of ∆ABD : area of ∆ADC = m : n.
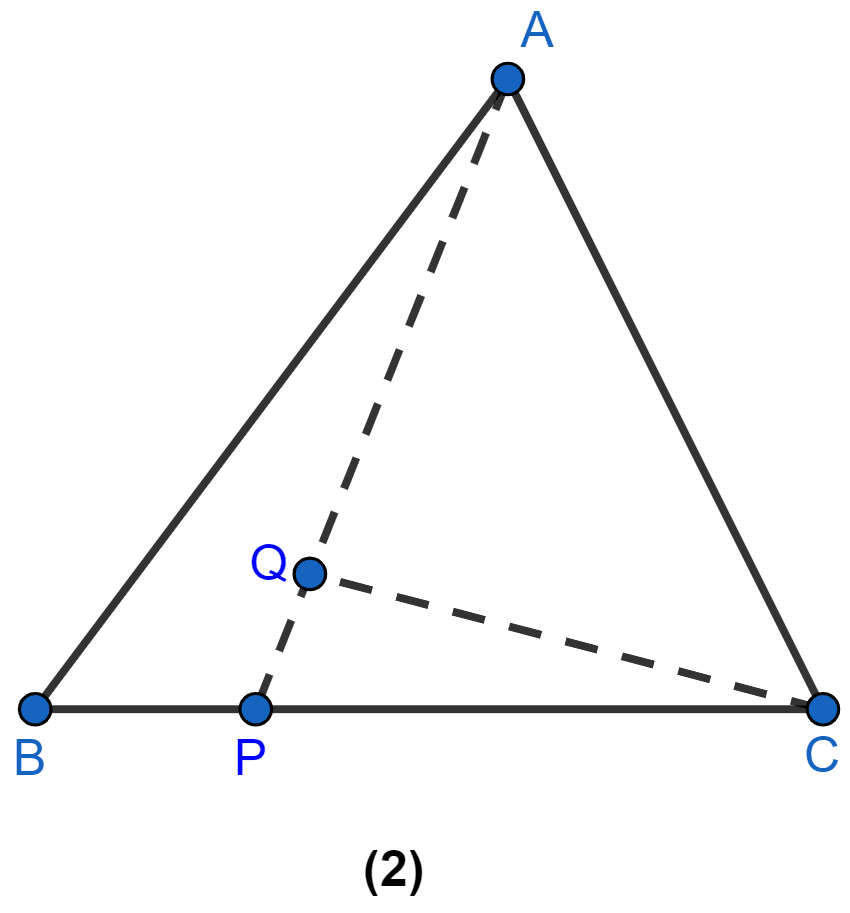
In the figure (2) given below, P is a point on the side BC of ∆ABC such that PC = 2BP, and Q is a point on AP such that QA = 5PQ, find area of ∆AQC : area of ∆ABC.
In figure (1) given below, area of parallelogram ABCD is 29 cm2. Calculate the height of parallelogram ABEF if AB = 5.8 cm.

In figure (2) given below, area of ∆ABD is 24 sq. units. If AB = 8 units, find the height of △ABC.
