Mathematics
In figure (1) given below, area of parallelogram ABCD is 29 cm2. Calculate the height of parallelogram ABEF if AB = 5.8 cm.

Theorems on Area
16 Likes
Answer
||gm ABCD and ||gm ABEF are on same base (AB) and between the same parallel lines AB and DE, so their areas are equal.
Area of ||gm ABEF = Area of ||gm ABCD = 29 cm2.
Area of ||gm ABEF = base × height
⇒ 29 = AB × height
⇒ 29 = 5.8 × height
⇒ Height =
= 5 cm.
The height of parallelogram ABEF is 5 cm.
Answered By
10 Likes
Related Questions
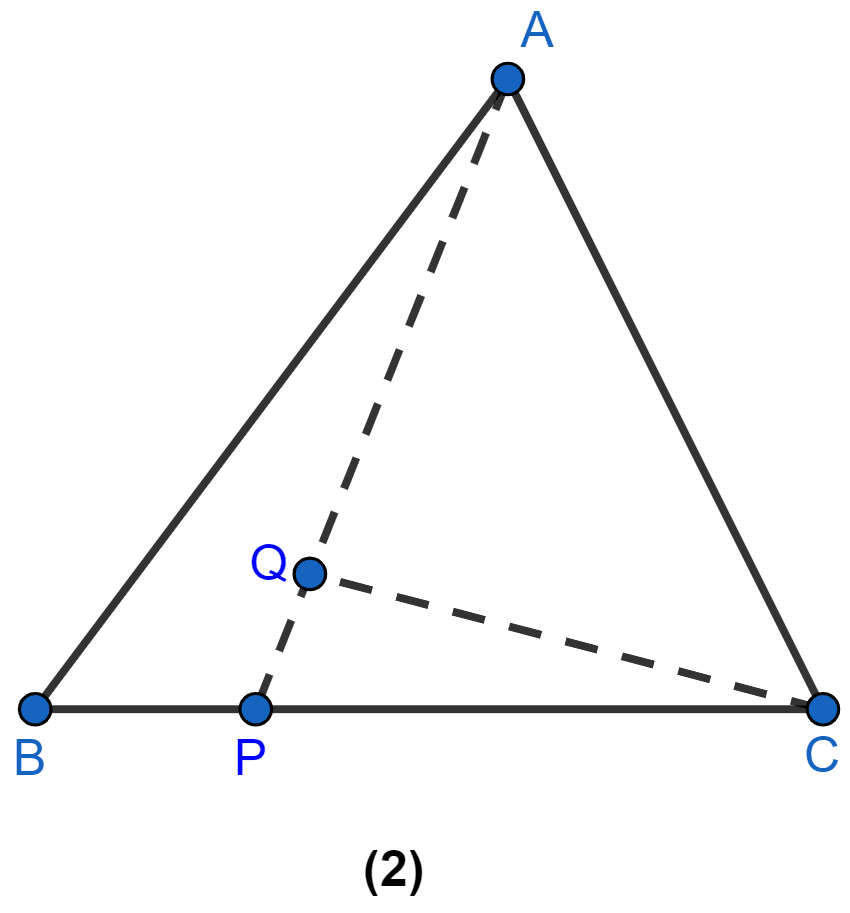
In the figure (2) given below, P is a point on the side BC of ∆ABC such that PC = 2BP, and Q is a point on AP such that QA = 5PQ, find area of ∆AQC : area of ∆ABC.
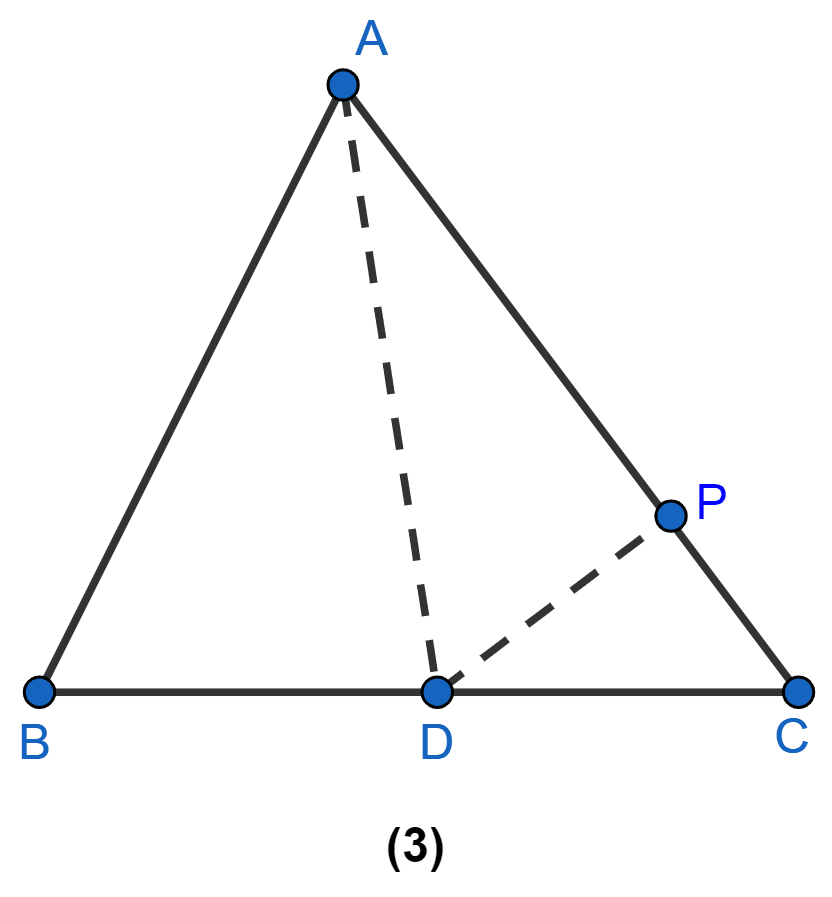
In the figure (3) given below, AD is a median of △ABC and P is a point in AC such that area of △ADP : area of △ABD = 2 : 3. Find
(i) AP : PC
(ii) area of △PDC : area of △ABC
In figure (2) given below, area of ∆ABD is 24 sq. units. If AB = 8 units, find the height of △ABC.

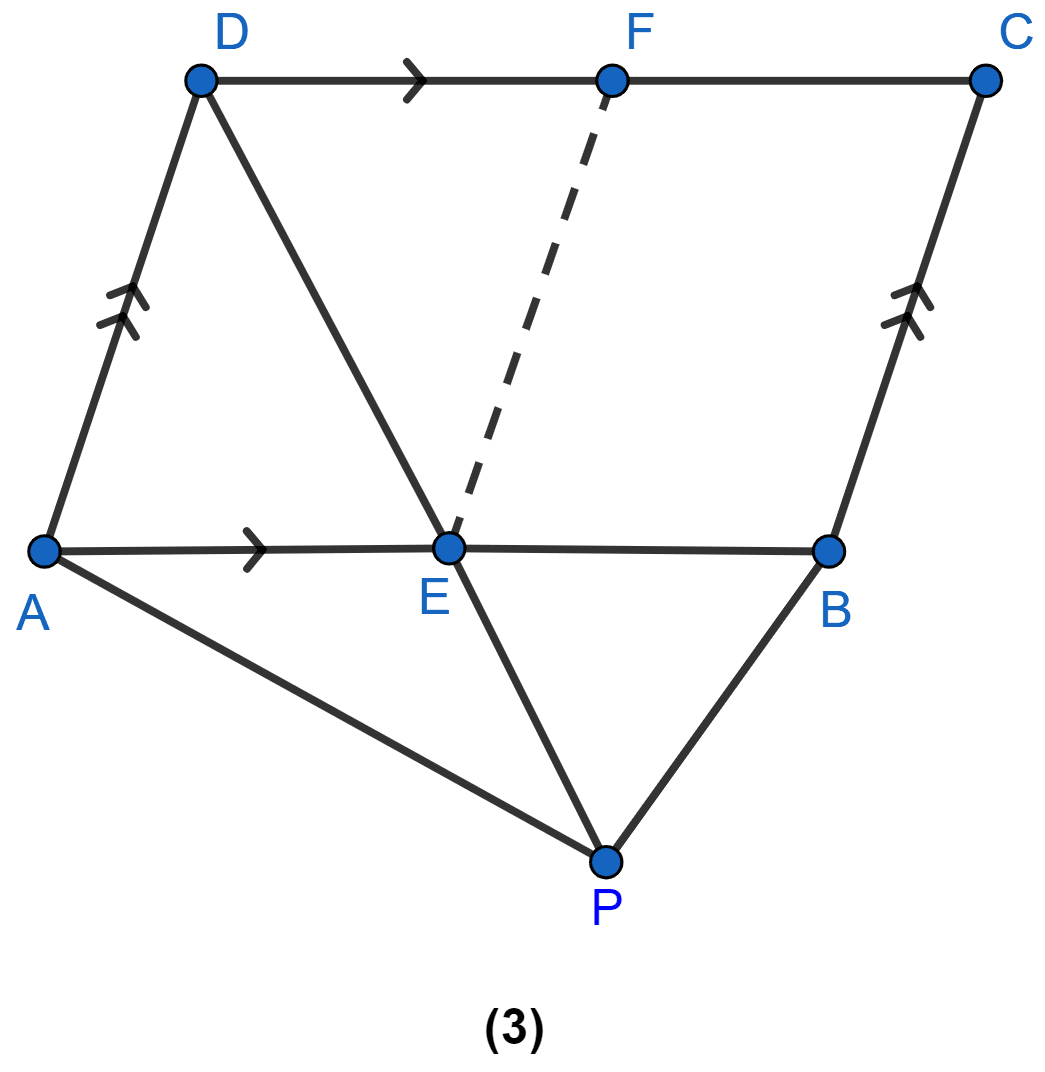
In figure (3) given below, E and F are midpoints of sides AB and CD, respectively, of parallelogram ABCD. If the area of parallelogram ABCD is 36 cm2,
(i) state the area of ∆APD.
(ii) Name the parallelogram whose area is equal to the area of ∆APD.