Mathematics
In the figure (2) given below, O is any point inside a parallelogram ABCD. Prove that (i) area of ∆OAB + area of ∆OCD = area of || gm ABCD. (ii) area of ∆OBC + area of ∆OAD = area of || gm ABCD.
Related Questions
In the figure (2) given below, DE || BC. Prove that
(i) area of ∆ACD = area of ∆ABE
(ii) area of ∆OBD = area of ∆OCE.

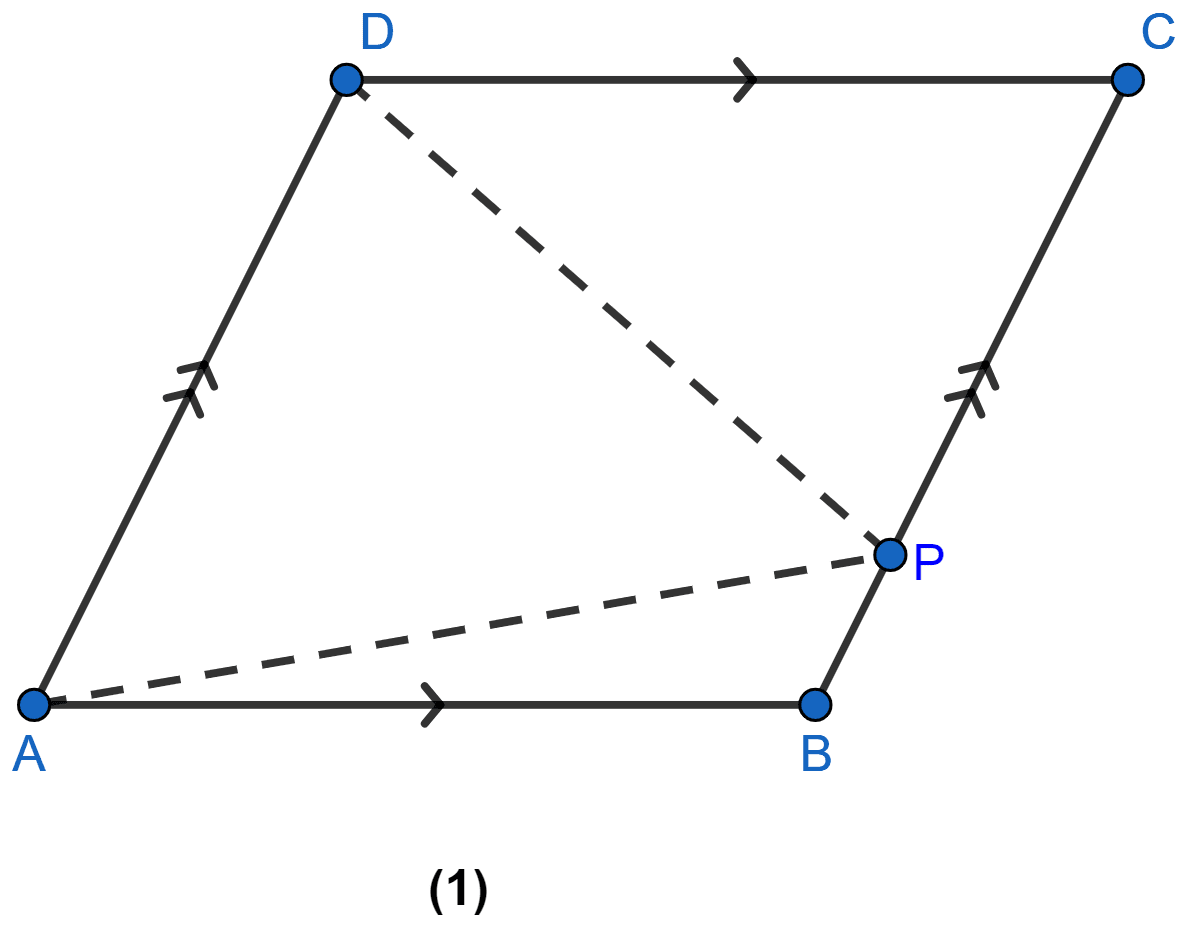
In figure (1) given below, ABCD is a parallelogram and P is any point in BC. Prove that, Area of ∆ABP + area of ∆DPC = Area of ∆APD.
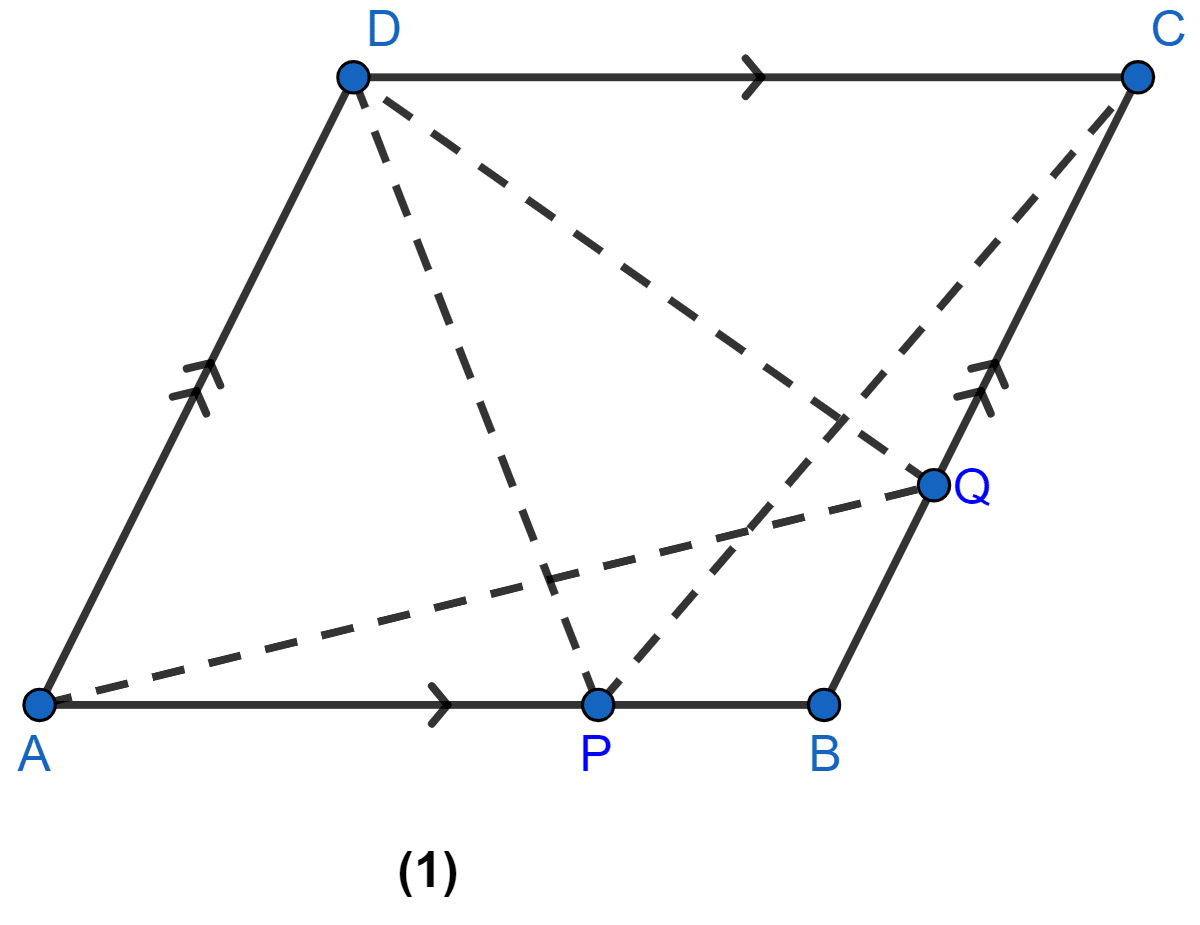
In figure (1) given below, ABCD is a parallelogram. P, Q are any two points on the sides AB and BC respectively. Prove that
area of ∆CPD = area of ∆AQD.