Mathematics
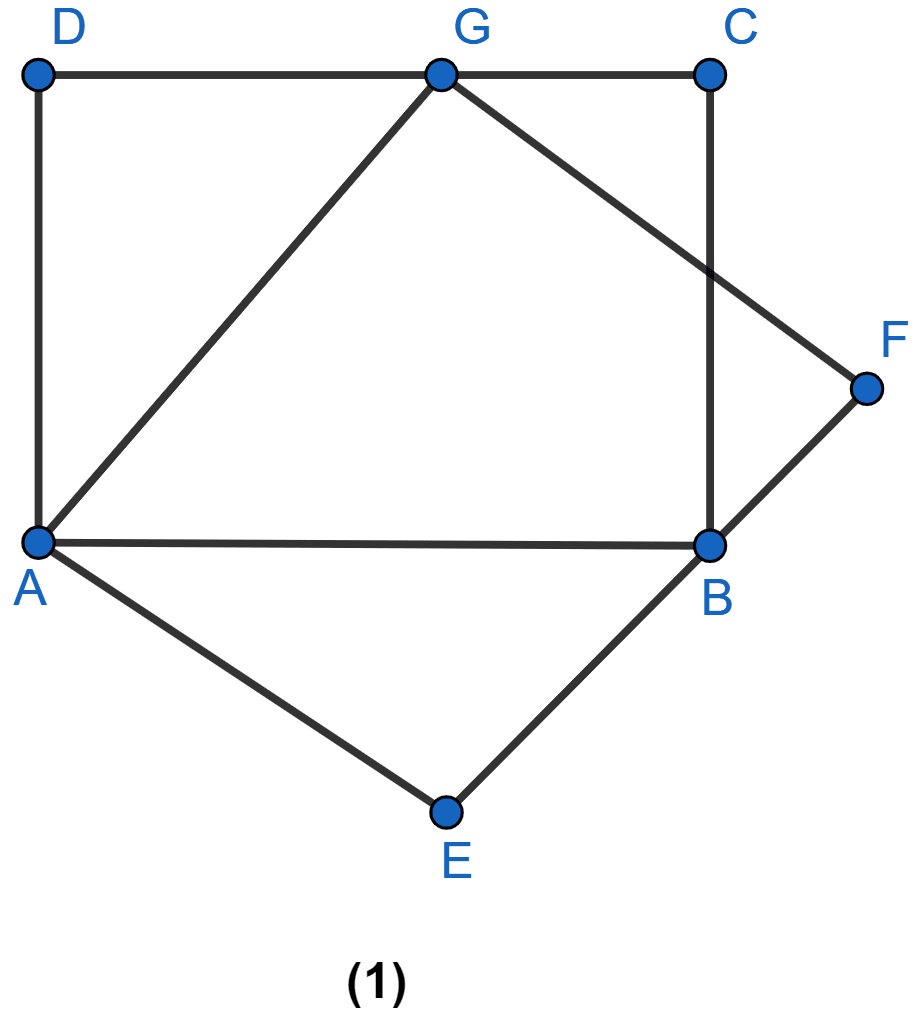
In the figure (1) given, ABCD and AEFG are two parallelograms. Prove that area of || gm ABCD = area of || gm AEFG.
Theorems on Area
14 Likes
Answer
(a) Join BG.
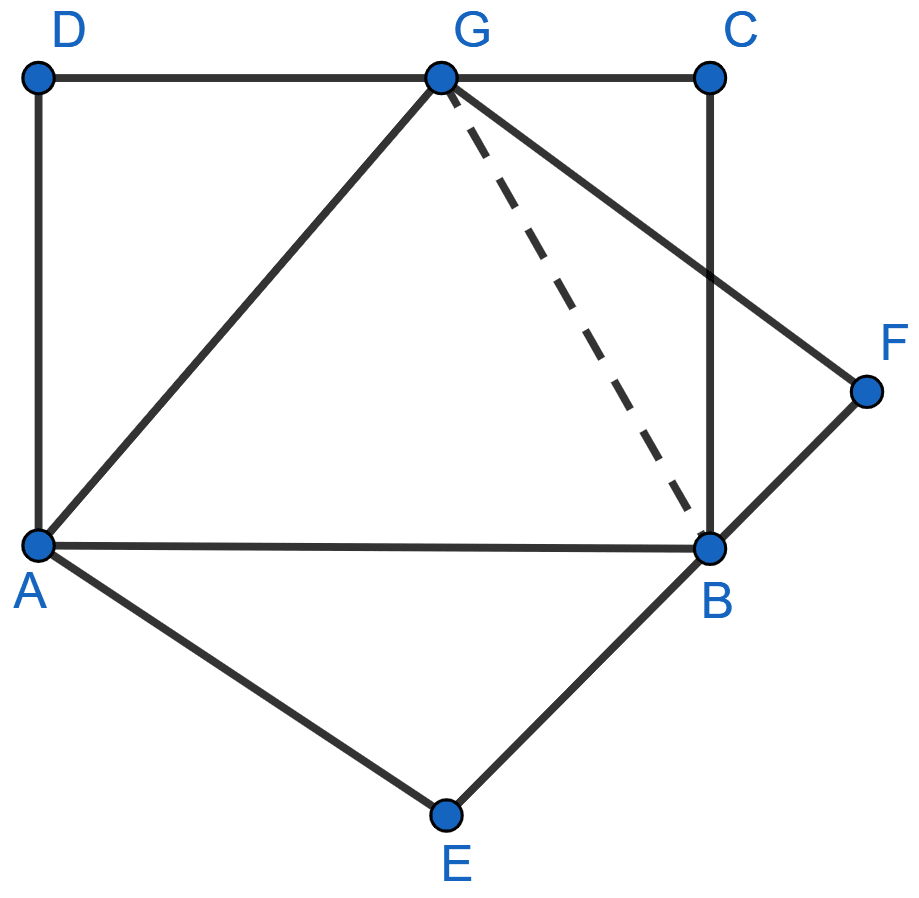
We know that,
Since, ∆ABG and || gm ABCD lie on same base AB and between same parallel lines AB and CD.
Area of ∆ABG = Area of ||gm ABCD ……(i)
Since, ∆ABG and || gm AEFG lie on same base AG and between same parallel lines AG and EF.
Area of ∆ABG = Area of ||gm AEFG ……(ii)
From (i) and (ii) we get,
Area of || gm ABCD = Area of || gm AEFG
⇒ Area of || gm ABCD = Area of || gm AEFG
Hence, proved that area of || gm ABCD = area of || gm AEFG.
Answered By
10 Likes
Related Questions
In figure (2) given below, DE is drawn parallel to the diagonal AC of the quadrilateral ABCD to meet BC produced at point E. Prove that area of quad. ABCD = area of ∆ABE.

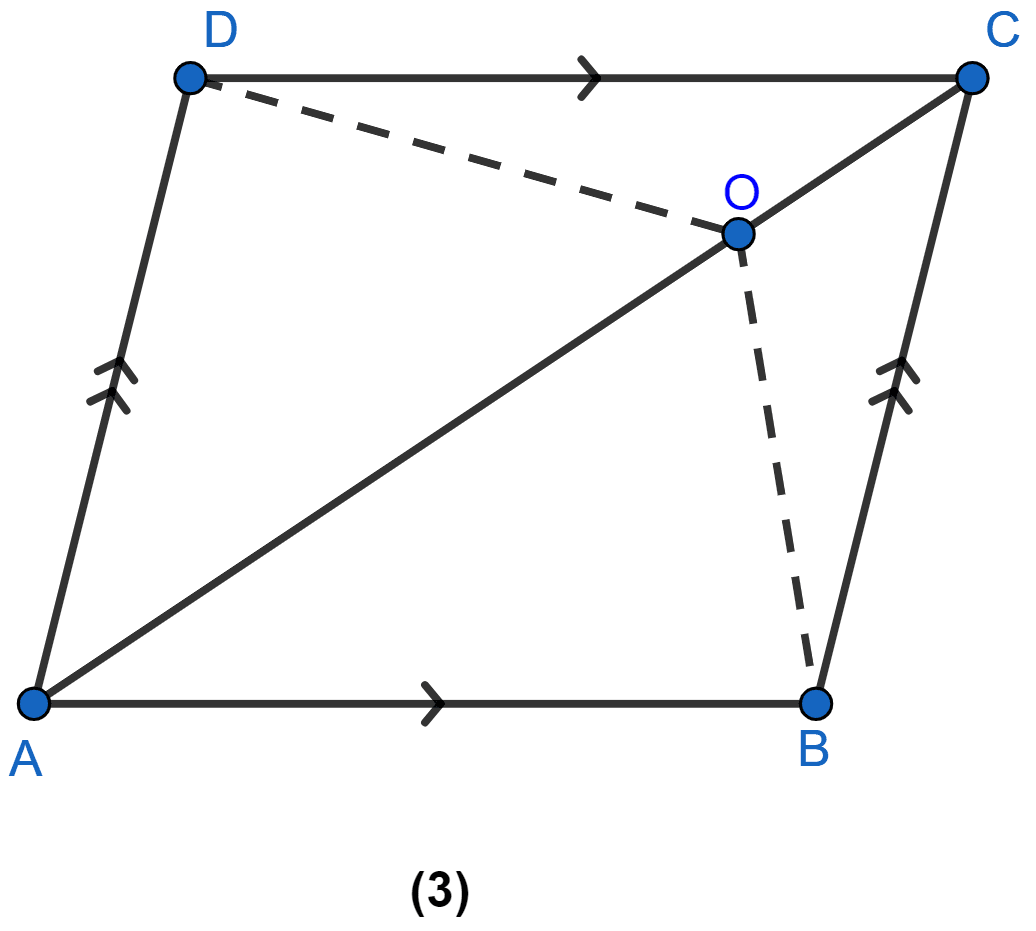
In the figure (3) given below, ABCD is a parallelogram. O is any point on the diagonal AC of the parallelogram. Show that the area of ∆AOB is equal to the area of ∆AOD.
In figure (2) given below, the side AB of the parallelogram ABCD is produced to E. A straight line through A is drawn parallel to CE to meet CB produced at F and parallelogram BFGE is completed. Prove that
area of || gm BFGE = area of || gm ABCD.
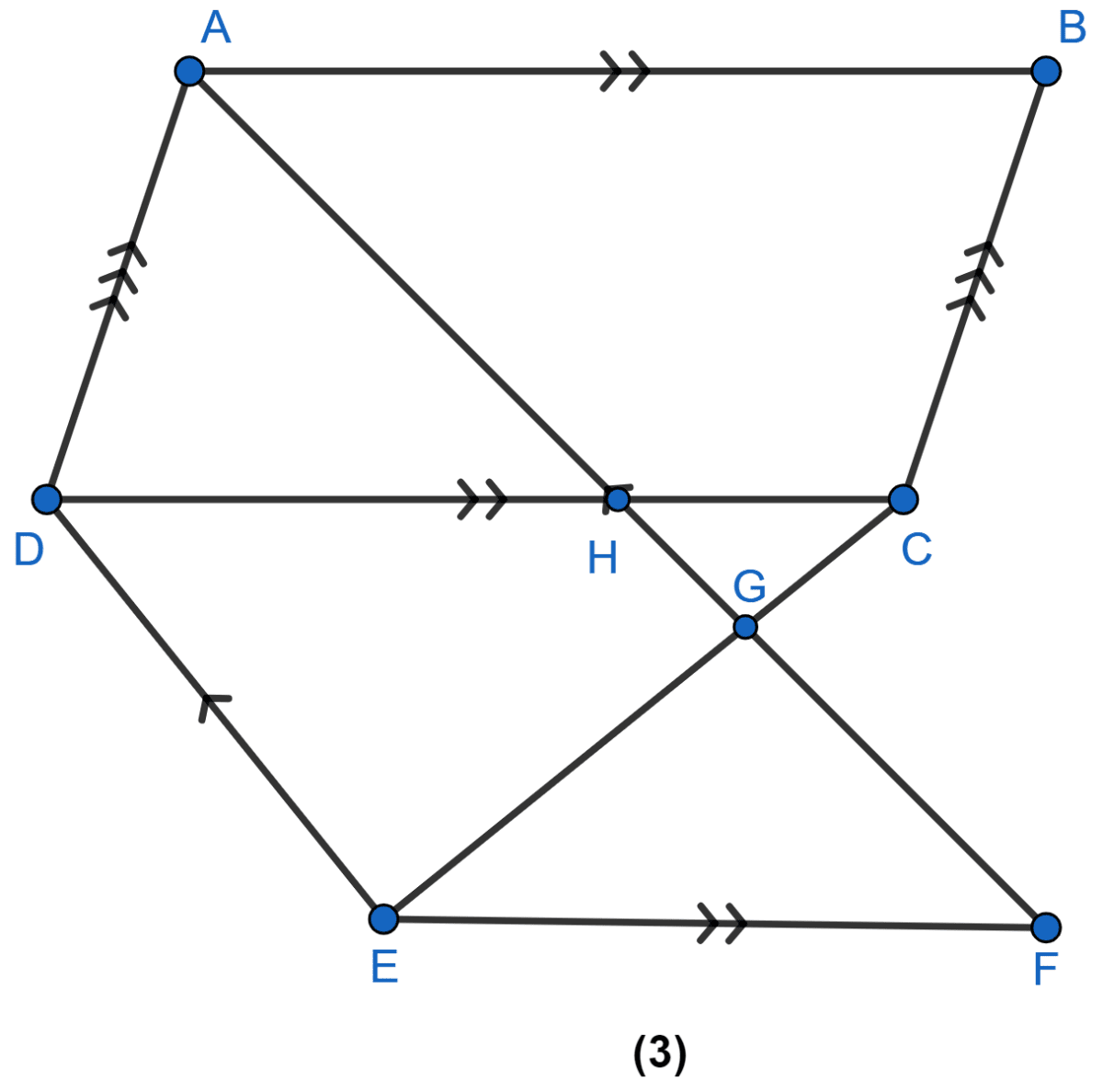
In figure (3) given below, AB || DC || EF, AD || BE and DE || AF. Prove that the area of DEFH is equal to the area of ABCD.