Mathematics
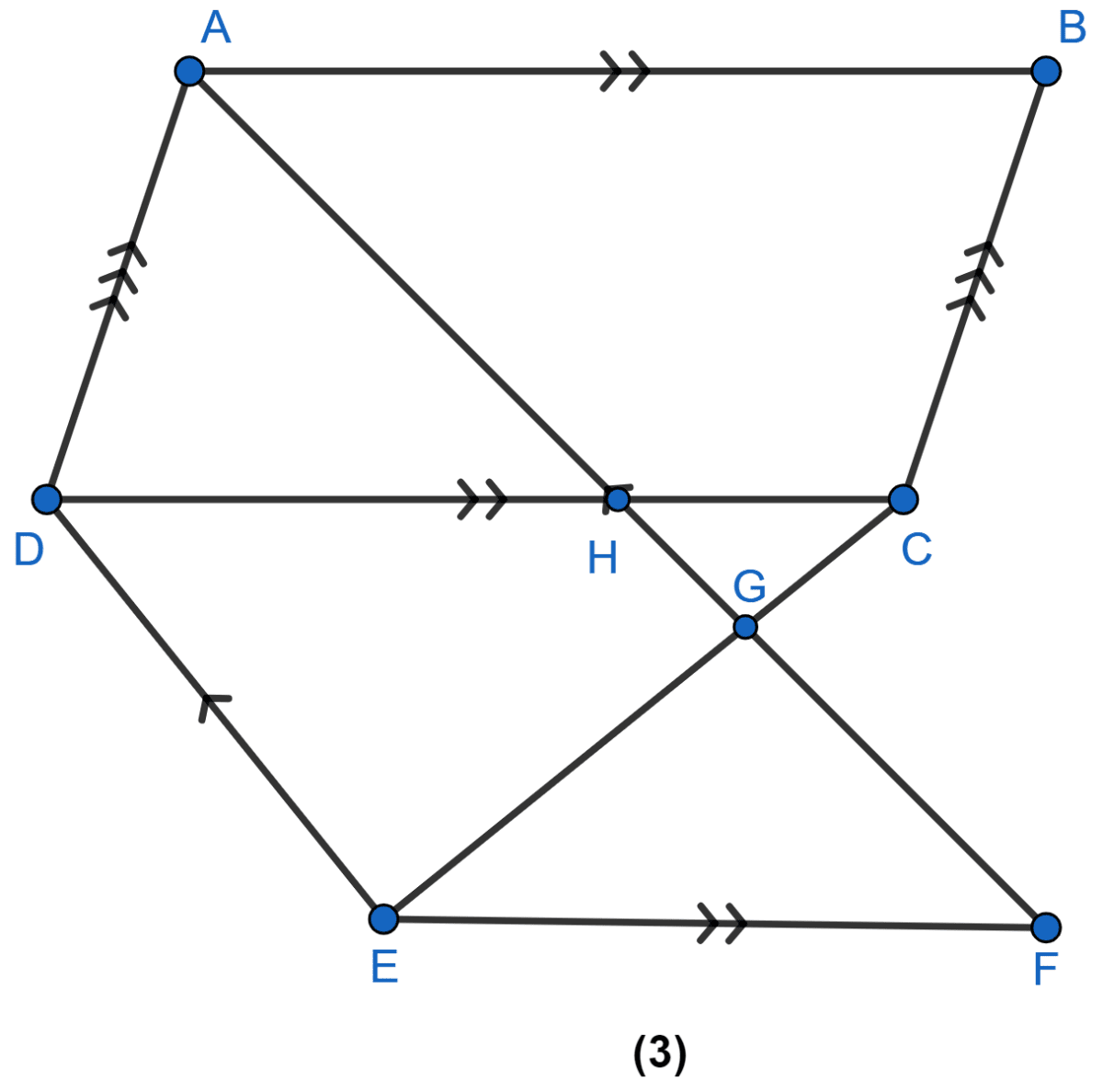
In figure (3) given below, AB || DC || EF, AD || BE and DE || AF. Prove that the area of DEFH is equal to the area of ABCD.
Theorems on Area
19 Likes
Answer
We know that,
AD || BE ⇒ AD || EG
ED || FA ⇒ ED || GA
Since, opposite sides are parallel.
Hence, ADEG is a parallelogram.
Since || gm ABCD and || gm ADEG lie on same base AD and between same parallel lines AD and EB,
area of || gm ABCD = area of ||gm ADEG ……. (i)
We know that,
ED || FA ⇒ DE || FH
DH || EF
Since, opposite sides are parallel.
Hence, DEFH is a parallelogram.
Since || gm DEFH and || gm ADEG lie on same base DE and between same parallel lines DE and FA,
area of ||gm DEFH = area of ||gm ADEG ……. (ii)
From (i) and (ii) we get,
⇒ area of ||gm ABCD = area of ||gm DEFH
Hence, proved that area of ||gm ABCD = area of ||gm DEFH.
Answered By
9 Likes
Related Questions
ABCD is a rectangle and P is the mid-point of AB. DP is produced to meet CB at Q. Prove that the area of rectangle ABCD = area of ∆DQC.
Any point D is taken on the side BC of a ∆ABC and AD is produced to E such that AD = DE, prove that area of ∆BCE = area of ∆ABC.
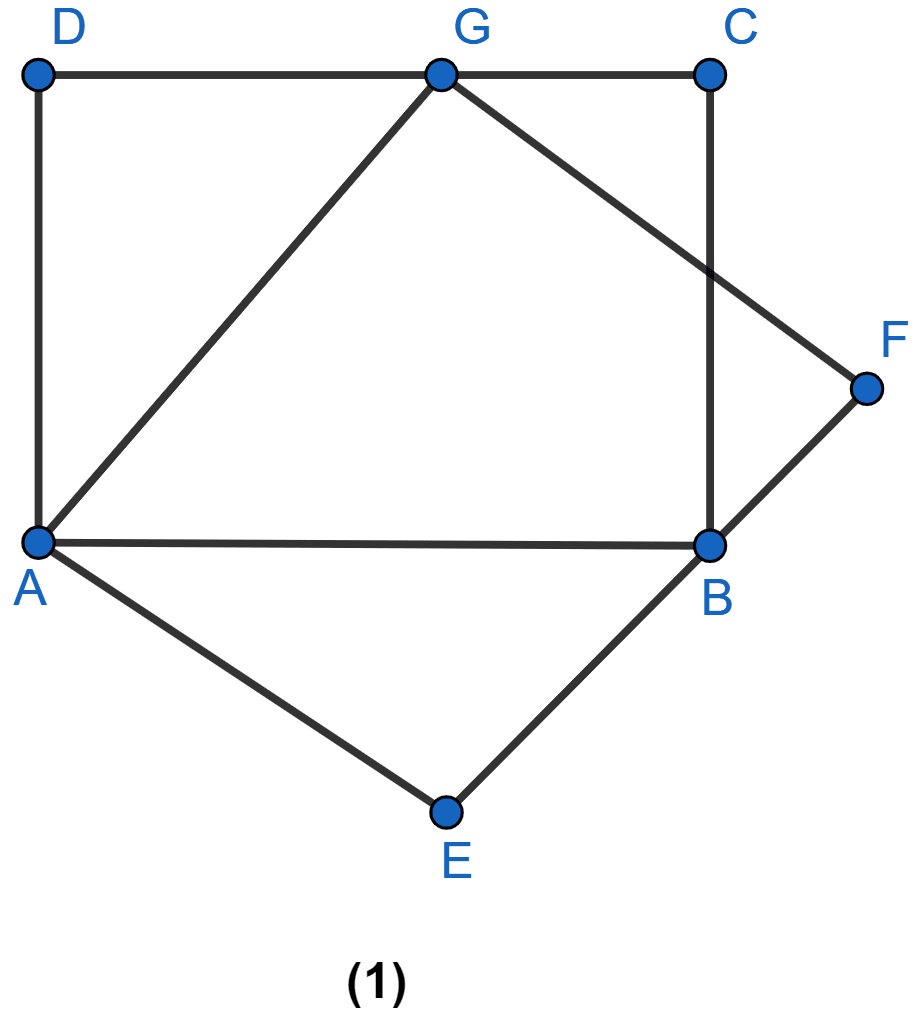
In the figure (1) given, ABCD and AEFG are two parallelograms. Prove that area of || gm ABCD = area of || gm AEFG.
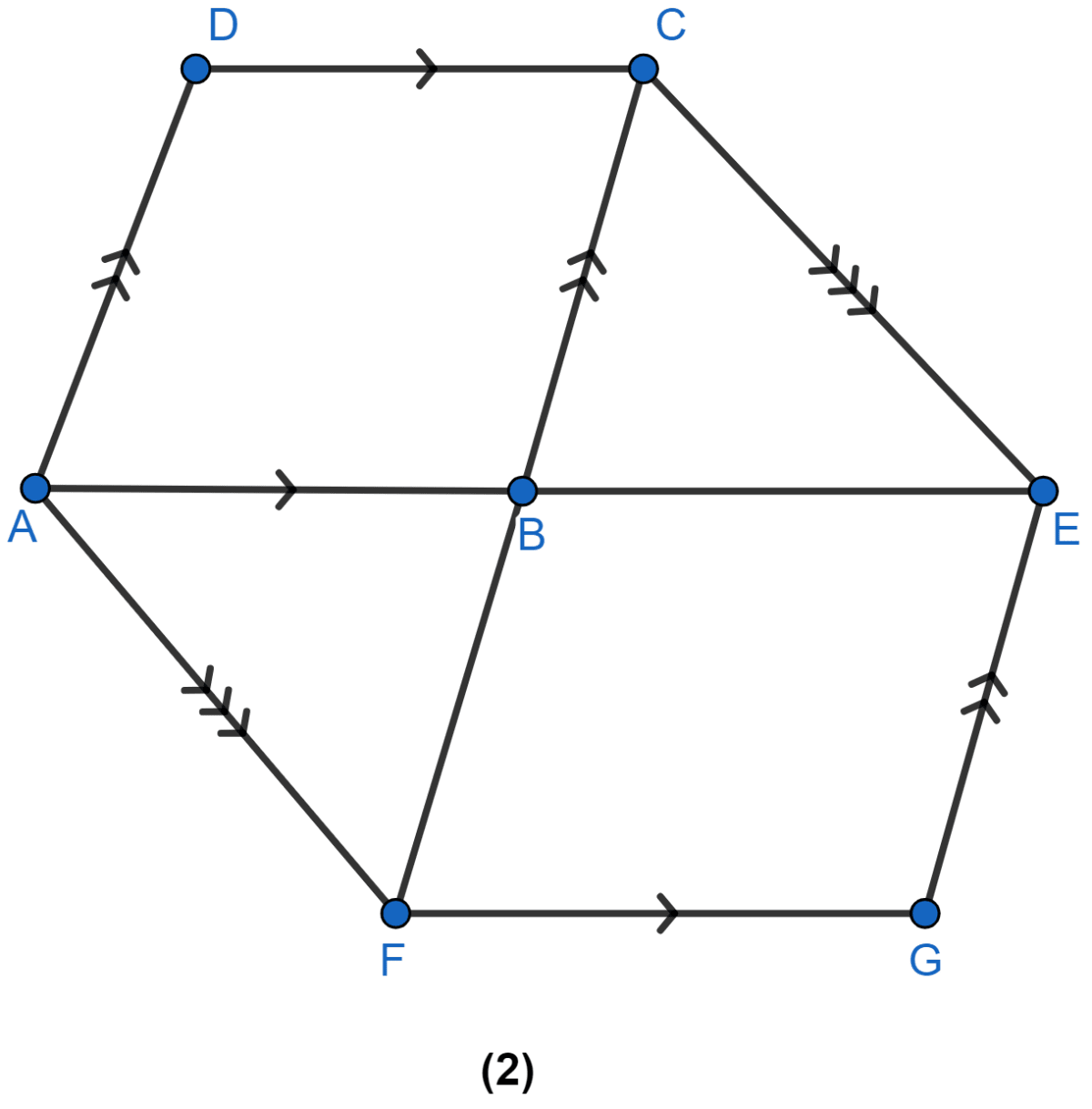
In figure (2) given below, the side AB of the parallelogram ABCD is produced to E. A straight line through A is drawn parallel to CE to meet CB produced at F and parallelogram BFGE is completed. Prove that
area of || gm BFGE = area of || gm ABCD.
