Mathematics
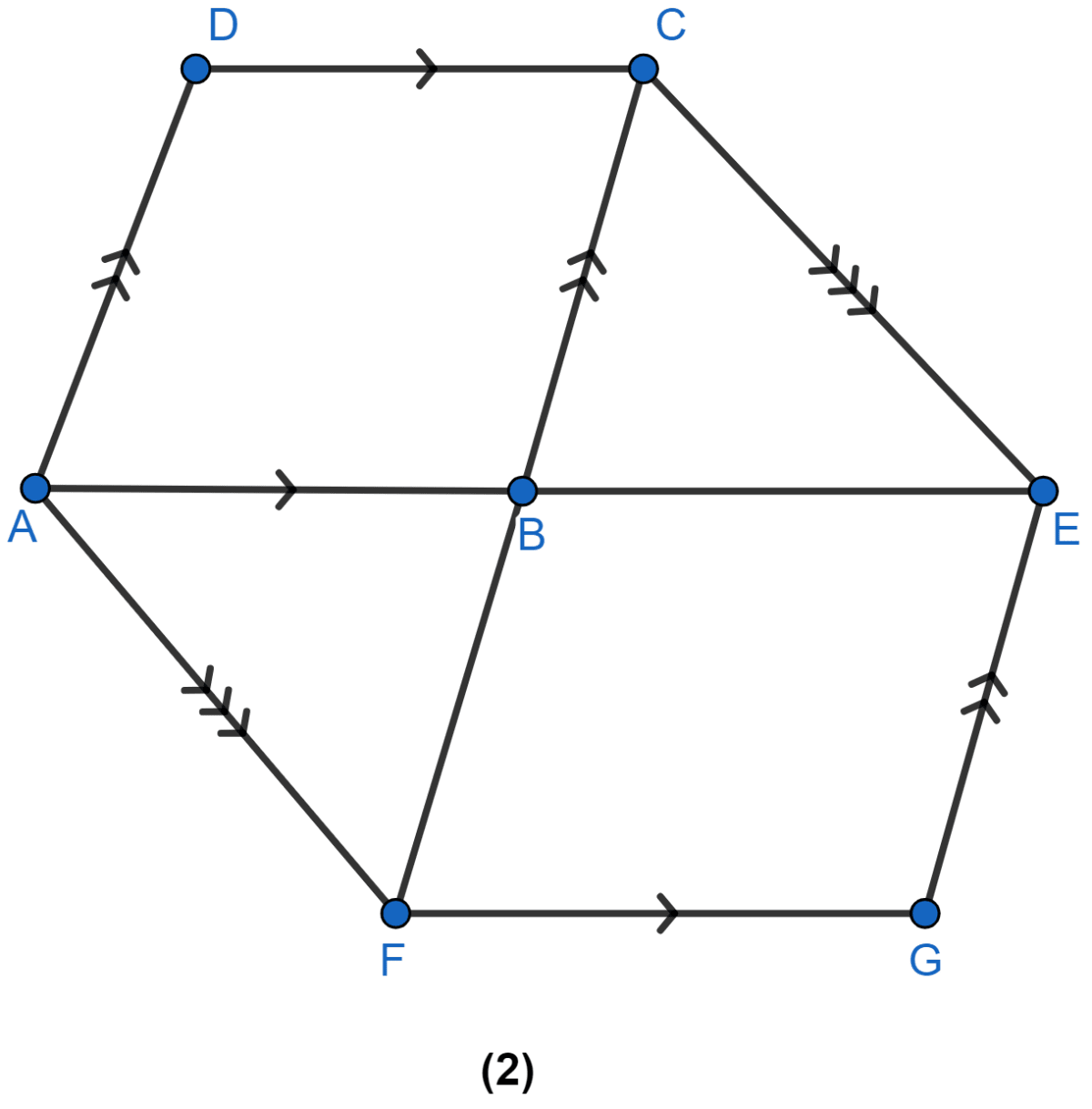
In figure (2) given below, the side AB of the parallelogram ABCD is produced to E. A straight line through A is drawn parallel to CE to meet CB produced at F and parallelogram BFGE is completed. Prove that
area of || gm BFGE = area of || gm ABCD.
Theorems on Area
16 Likes
Answer
Join AC and EF.
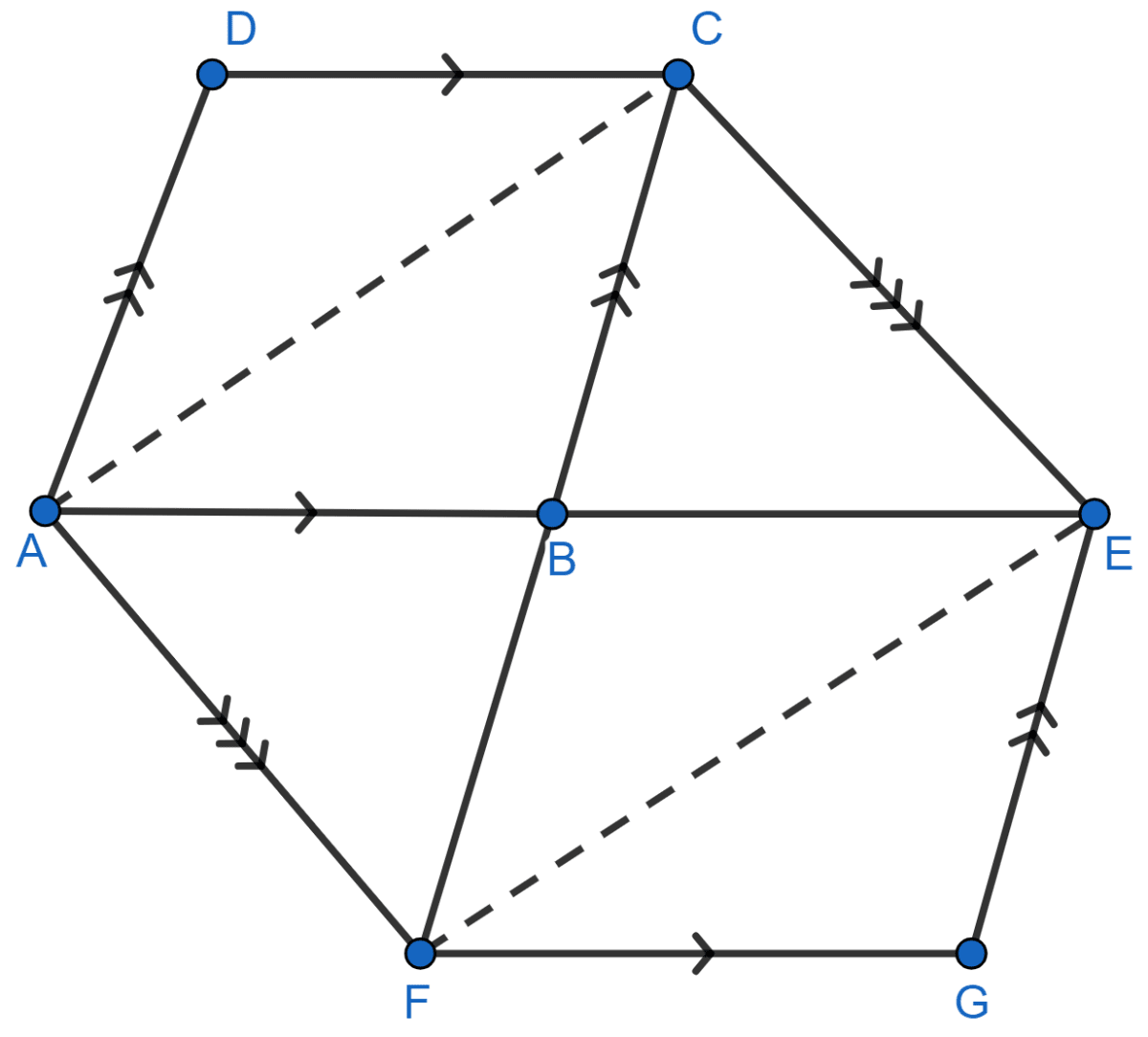
Since, ∆AFC and ∆AFE lie on same base AF and between same parallel lines AF and CE so,
area of ∆AFC = area of ∆AFE
Now, subtract area of ∆ABF on both sides,
area of (∆AFC - ∆ABF) = area of (∆AFE – ∆ABF)
area of ∆ABC = area of ∆BEF
2 area of ∆ABC = 2 area of ∆BEF …….(i)
From figure,
As || gm ABCD and ∆ABC lie on same base AB and between same parallel lines AB and DC.
Area of ∆ABC = Area of || gm ABCD
Area of || ABCD = 2 Area of ∆ABC ………(ii)
As || gm BFGE and ∆BEF lie on same base BE and between same parallel lines FG and BE.
Area of ∆BEF = Area of || gm BFGE
Area of || BFGE = 2 Area of ∆BEF ………(iii)
Substituting value from (ii) and (iii) in (i) we get,
Area of || ABCD = Area of || BFGE.
Hence, proved that area of || ABCD = area of || BFGE.
Answered By
14 Likes
Related Questions
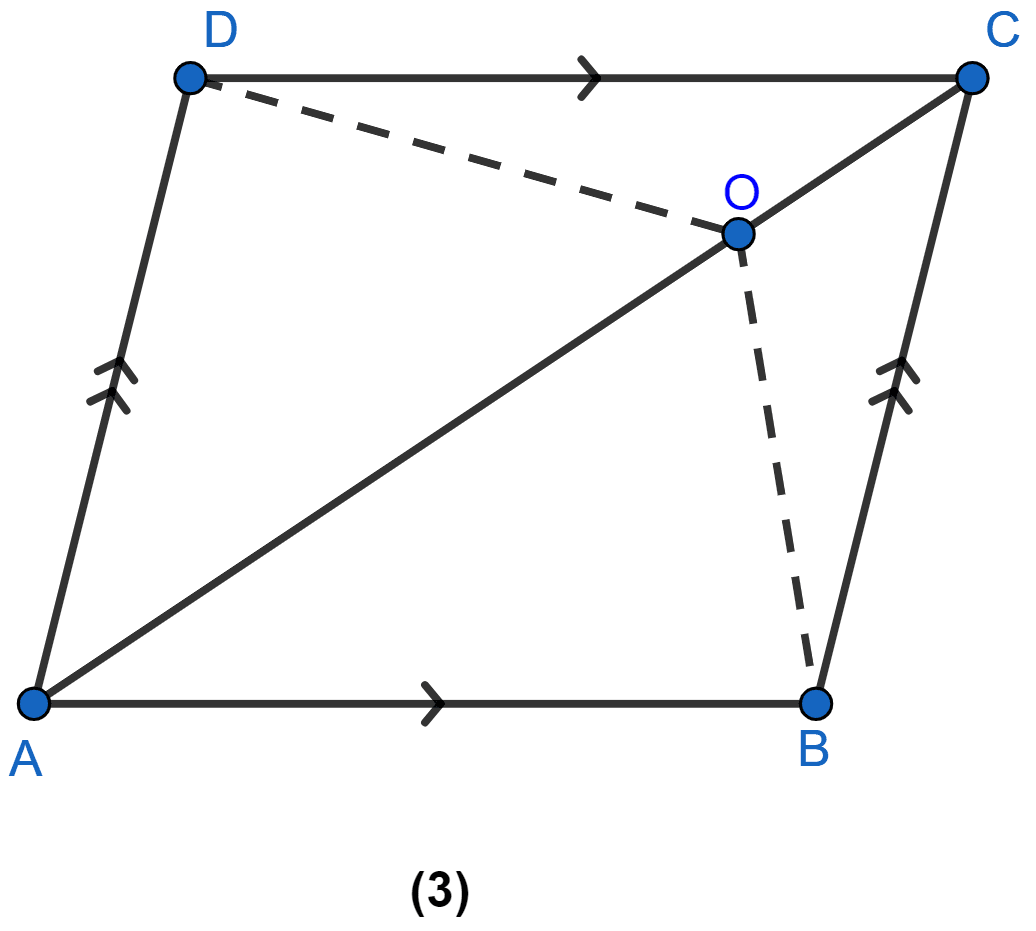
In the figure (3) given below, ABCD is a parallelogram. O is any point on the diagonal AC of the parallelogram. Show that the area of ∆AOB is equal to the area of ∆AOD.
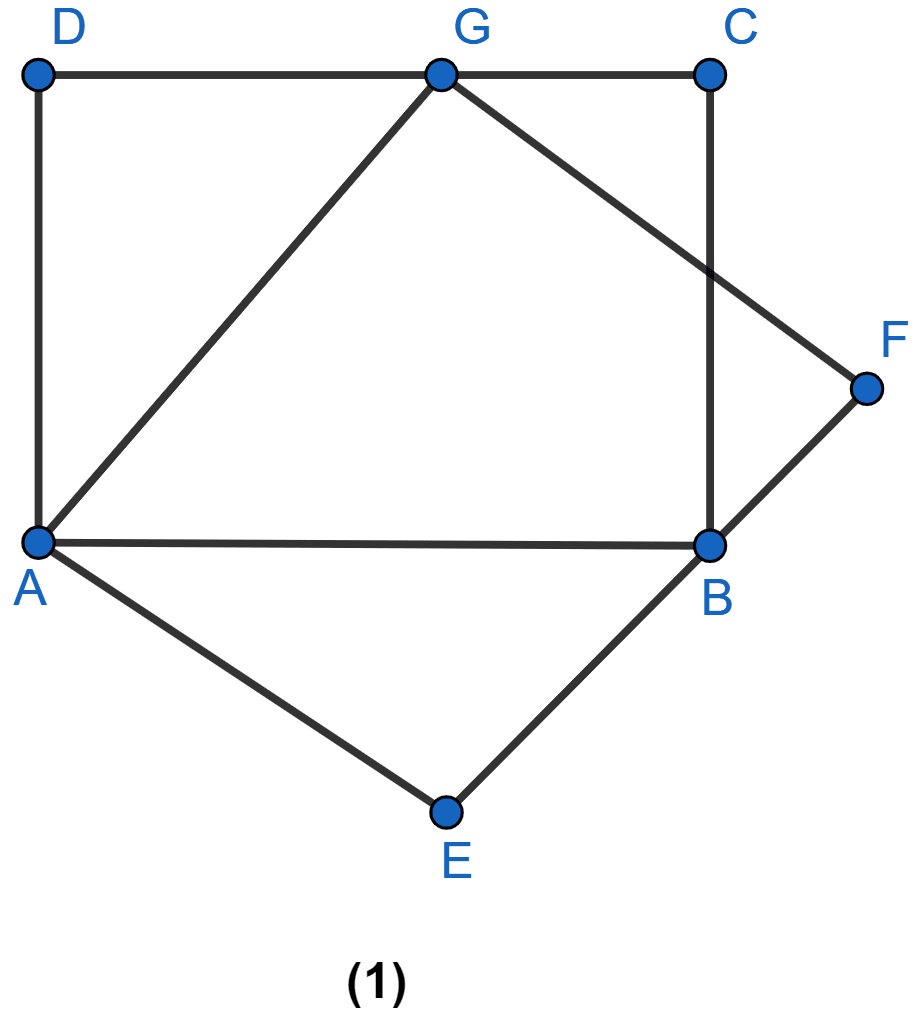
In the figure (1) given, ABCD and AEFG are two parallelograms. Prove that area of || gm ABCD = area of || gm AEFG.
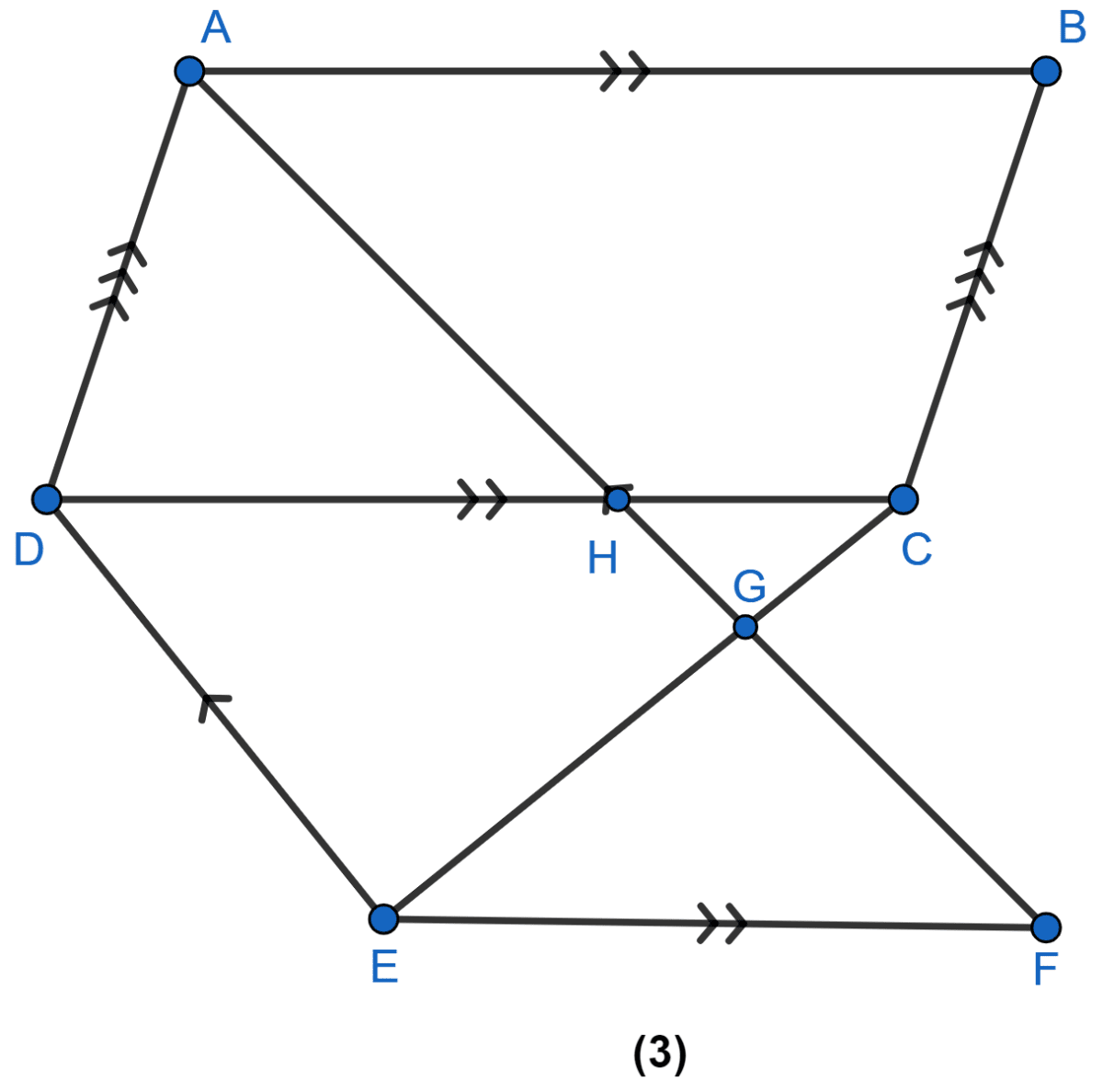
In figure (3) given below, AB || DC || EF, AD || BE and DE || AF. Prove that the area of DEFH is equal to the area of ABCD.
Any point D is taken on the side BC of a ∆ABC and AD is produced to E such that AD = DE, prove that area of ∆BCE = area of ∆ABC.