Mathematics
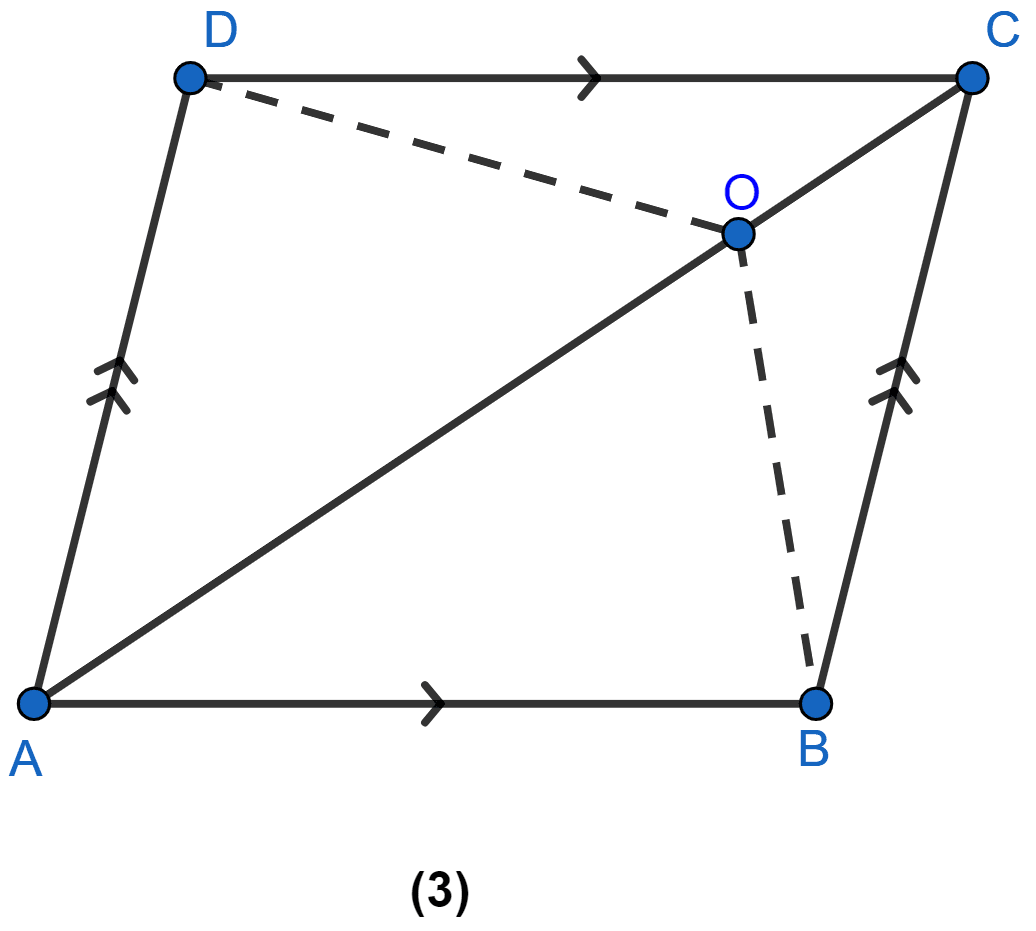
In the figure (3) given below, ABCD is a parallelogram. O is any point on the diagonal AC of the parallelogram. Show that the area of ∆AOB is equal to the area of ∆AOD.
Theorems on Area
26 Likes
Answer
Join BD, which meets AC at P.
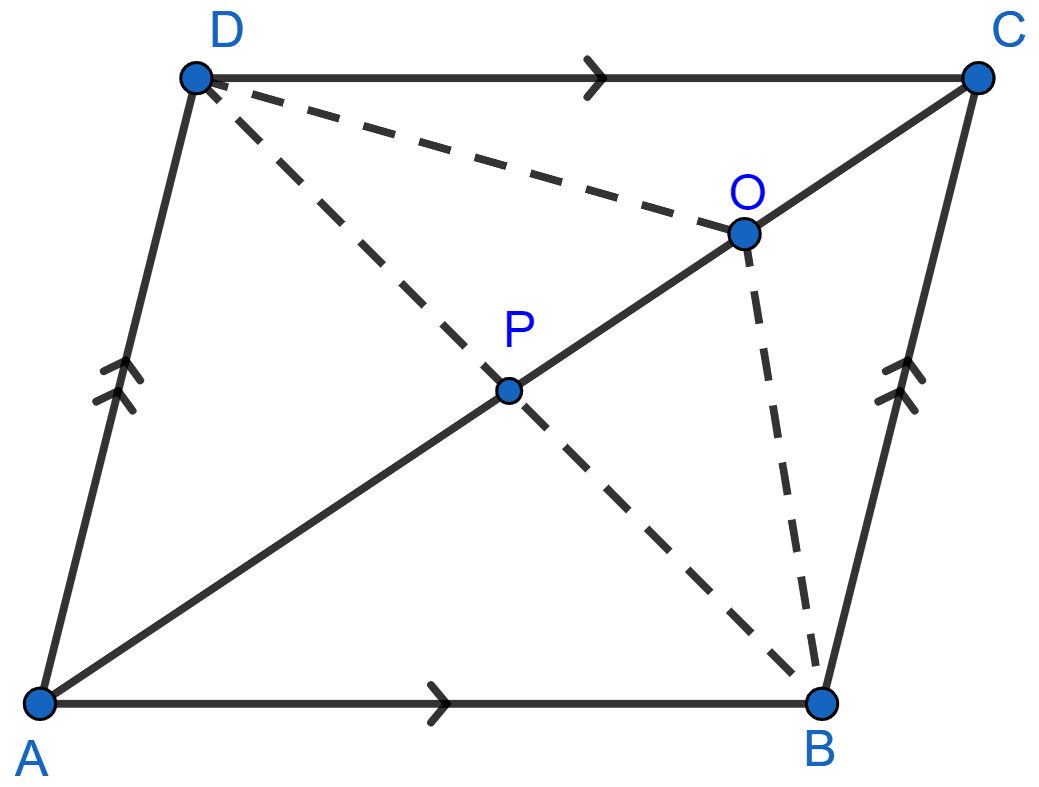
In ∆ABD, AP is the median (As P is mid-point of BD because diagonals of || gm bisect each other).
Since, median of triangle divides it into two triangles of equal area.
∴ Area of ∆ABP = Area of ∆ADP …….(i)
Similarly,
PO is median of ∆BOD,
∴ Area of ∆BOP = Area of ∆POD …….(ii)
Now, adding (i) and (ii), and we get
⇒ Area of ∆ABP + Area of ∆BOP = Area of ∆ADP + Area of ∆POD
⇒ Area of ∆AOB = Area of ∆AOD.
Hence, proved that area of ∆AOB = area of ∆AOD.
Answered By
21 Likes
Related Questions
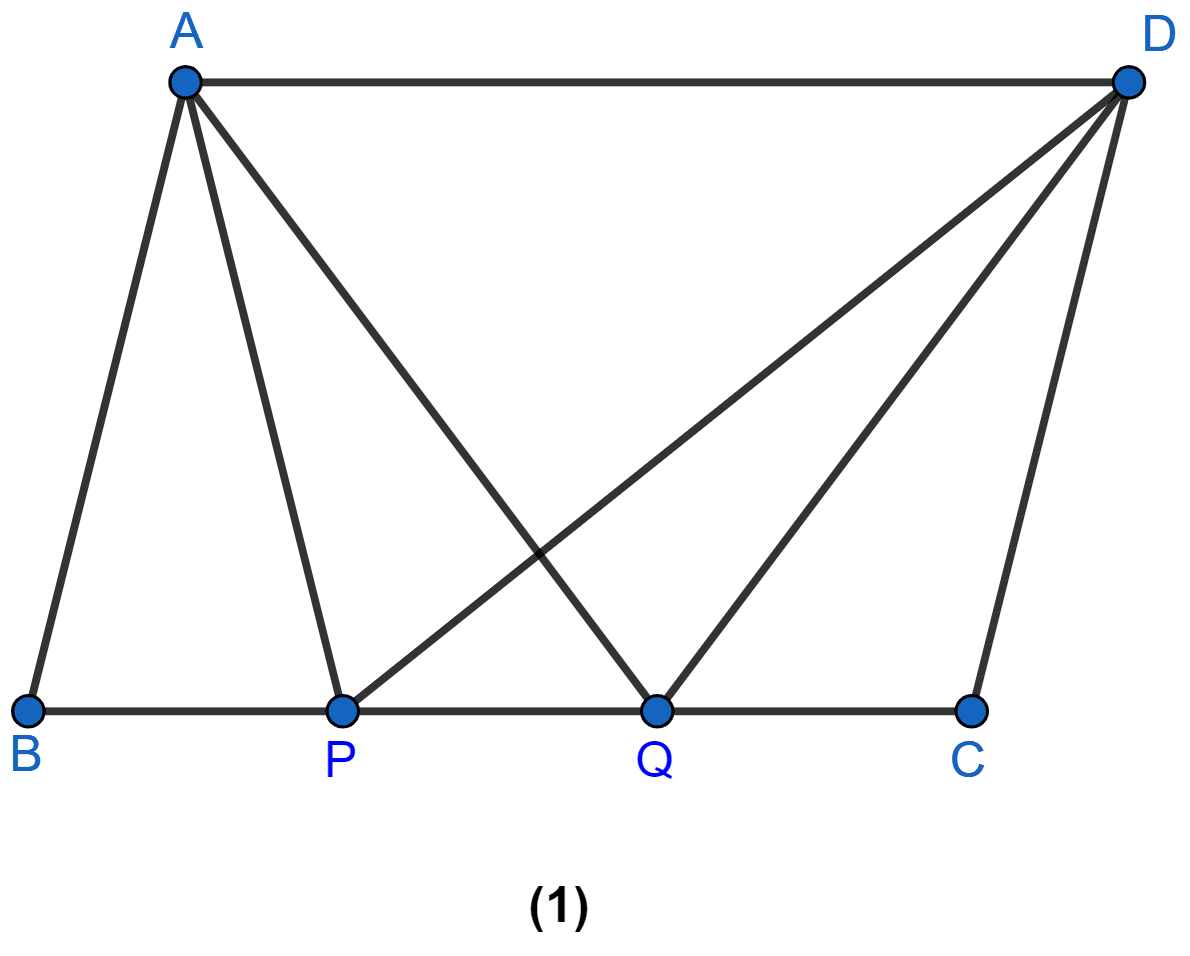
In figure (1) given below, ABCD is a parallelogram. Points P and Q on BC trisect BC into three equal parts. Prove that :
area of ∆APQ = area of ∆DPQ = (area of ||gm ABCD)
In figure (2) given below, DE is drawn parallel to the diagonal AC of the quadrilateral ABCD to meet BC produced at point E. Prove that area of quad. ABCD = area of ∆ABE.

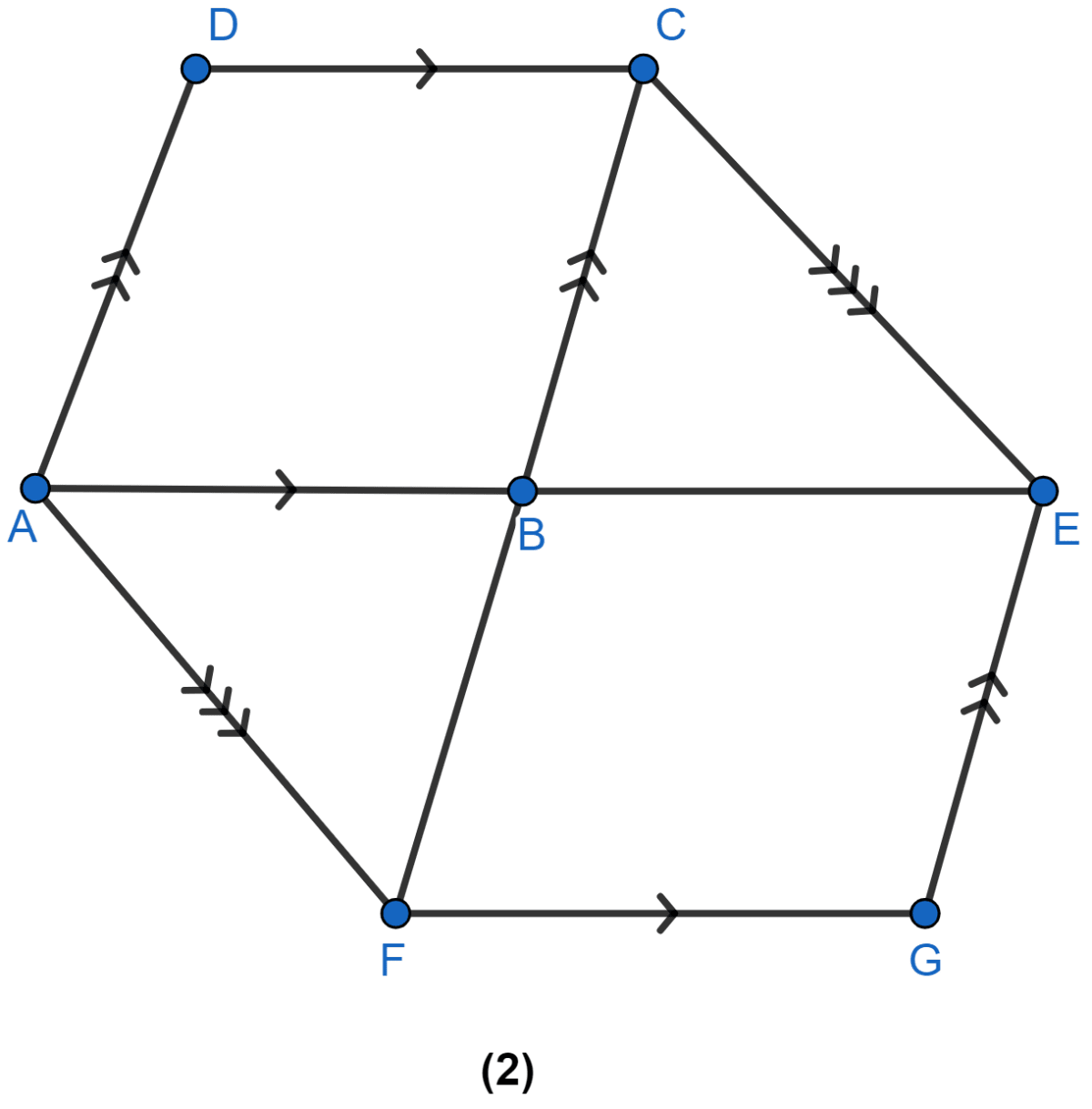
In the figure (1) given, ABCD and AEFG are two parallelograms. Prove that area of || gm ABCD = area of || gm AEFG.
In figure (2) given below, the side AB of the parallelogram ABCD is produced to E. A straight line through A is drawn parallel to CE to meet CB produced at F and parallelogram BFGE is completed. Prove that
area of || gm BFGE = area of || gm ABCD.