Mathematics
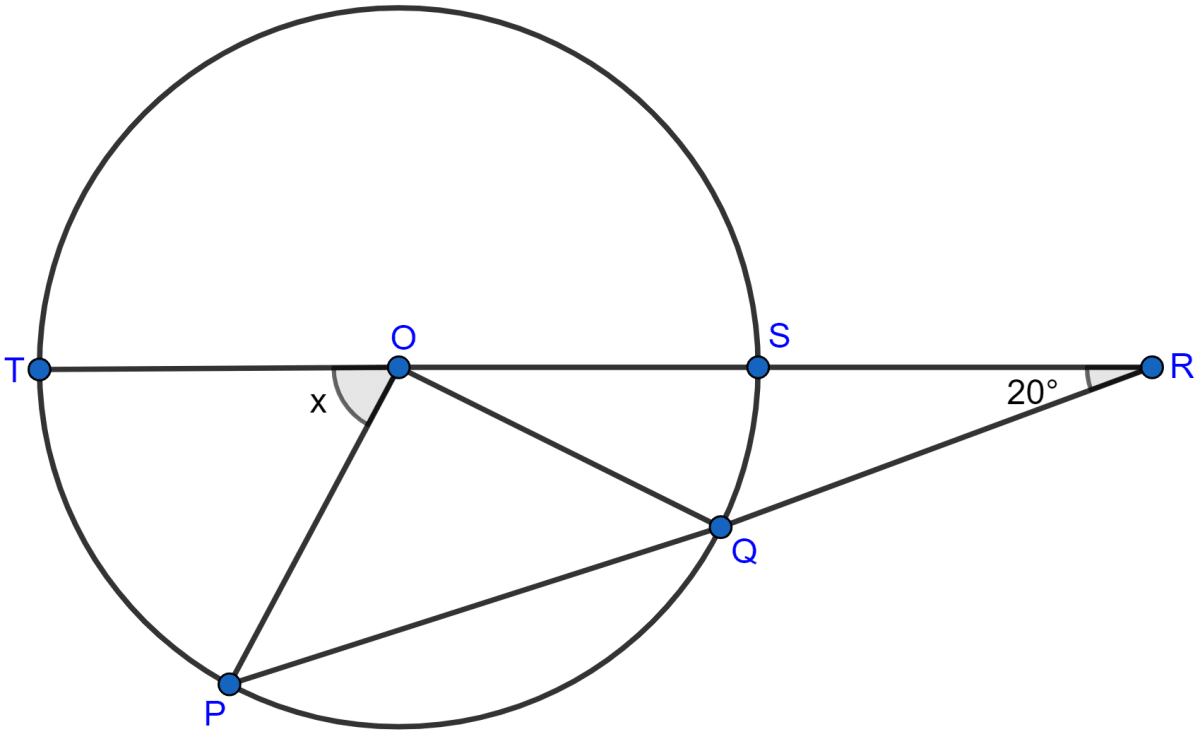
In the adjoining figure, O is the centre of the circle. If QR = OP and ∠ORP = 20°, find the value of 'x' giving reasons.
Answer
Given,
QR = OP ⇒ QR = OQ
⇒ ∠QOR = ∠ORQ = 20° (∵ angles opposite equal sides of a triangle are equal)
Exterior angle in a triangle is equal to the sum of two opposite interior angles.
∴ ∠OQP = ∠QOR + ∠ORQ = 20° + 20° = 40°.
As OP = OQ, ∠OPQ = ∠OQP
⇒ ∠OPQ = 40°
⇒ ∠OPR = 40°.
Exterior angle in a triangle is equal to the sum of two opposite interior angles.
∴ x = ∠TOP = ∠OPR + ∠ORP = 40° + 20° = 60°.
Hence, the value of x = 60°.
Related Questions
In the figure (i) given below, AC is a tangent to the circle with centre O. If ∠ADB = 55°, find x and y. Give reasons for your answers.
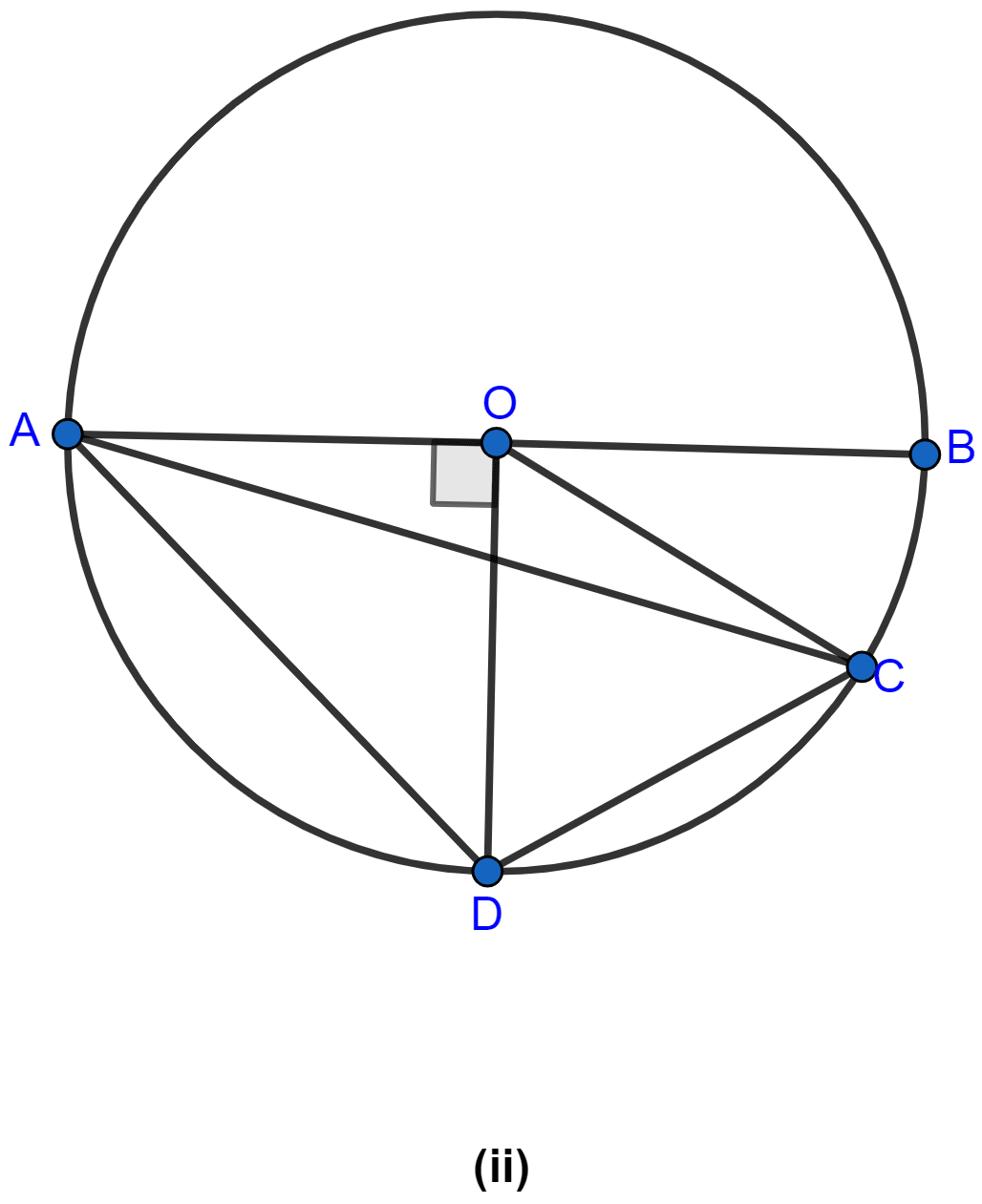
In the figure (ii) given below, AB is a diameter of a circle with centre O. OD is perpendicular to AB and C is a point on the arc DB. Find ∠BAD and ∠ACD.
In the figure (ii) given below, AB is a diameter of the semicircle ABCDE with centre O. If AE = ED and ∠BCD = 140°, find ∠AED and ∠EBD. Also prove that OE is parallel to BD.
In the figure (i) given below, triangle ABC is equilateral. Find ∠BDC and ∠BEC.
