Mathematics
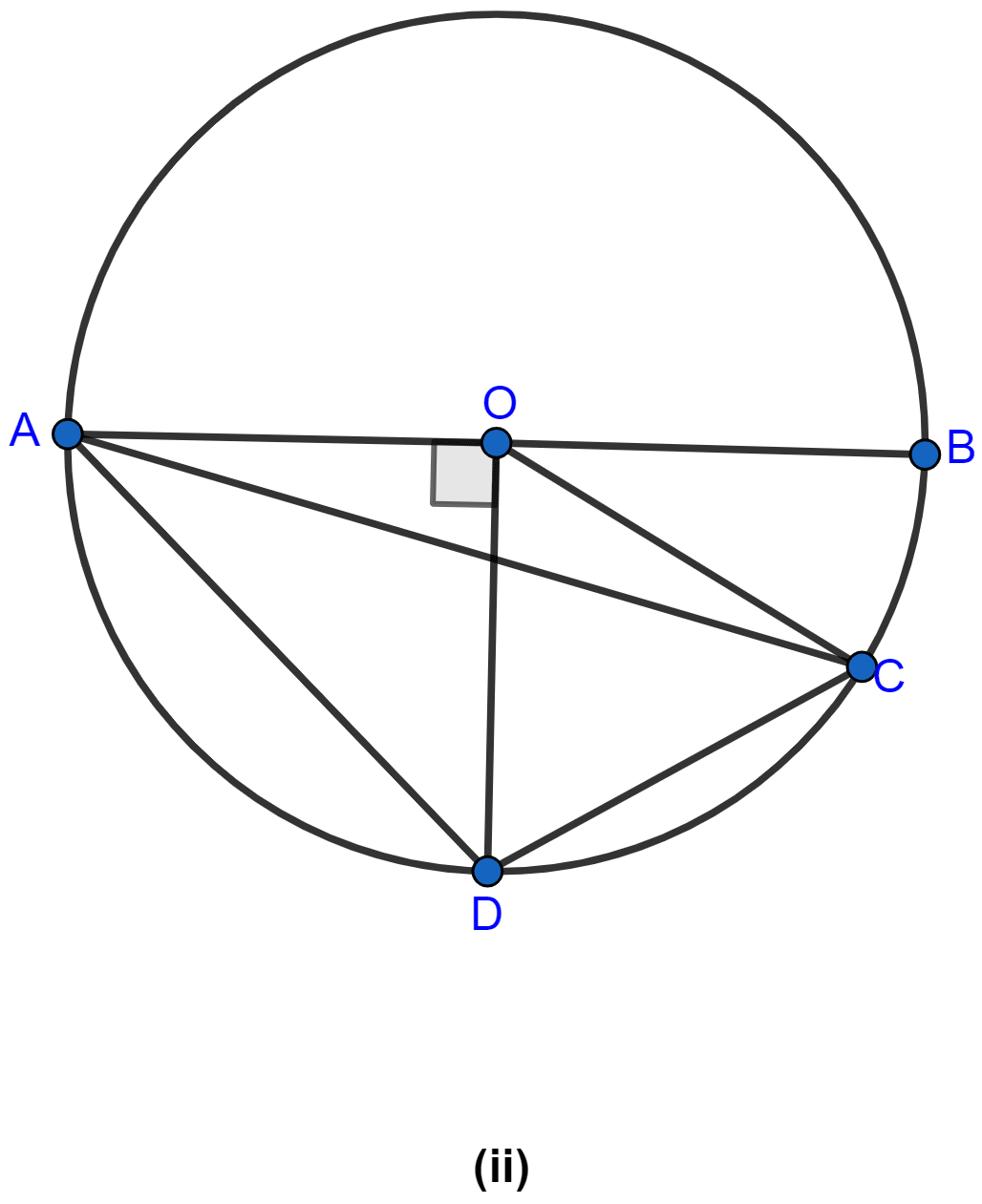
In the figure (ii) given below, AB is a diameter of a circle with centre O. OD is perpendicular to AB and C is a point on the arc DB. Find ∠BAD and ∠ACD.
Circles
23 Likes
Answer
In △AOD, ∠AOD = 90°.
OA = OD (Radii of the semi-circle)
∠OAD = ∠ODA (∵ angles opposite equal side are equal.)
We know that sum of angles in a triangle = 180°.
In △OAD,
⇒ ∠AOD + ∠OAD + ∠ODA = 180°
⇒ 90° + ∠OAD + ∠OAD = 180°
⇒ 90° + 2∠OAD = 180°
⇒ 2∠OAD = 180° - 90°
⇒ ∠OAD = = 45°.
From figure,
∠BAD = ∠OAD = 45°.
Arc AD subtends ∠AOD at the centre and ∠ACD at the remaining part of the circle.
∠AOD = 2∠ACD (∵ angle subtended on centre is double the angle subtended at remaining part of the circle.)
⇒ 90° = 2∠ACD
⇒ ∠ACD = = 45°.
Hence, the value of ∠BAD = 45° and ∠ACD = 45°.
Answered By
14 Likes
Related Questions
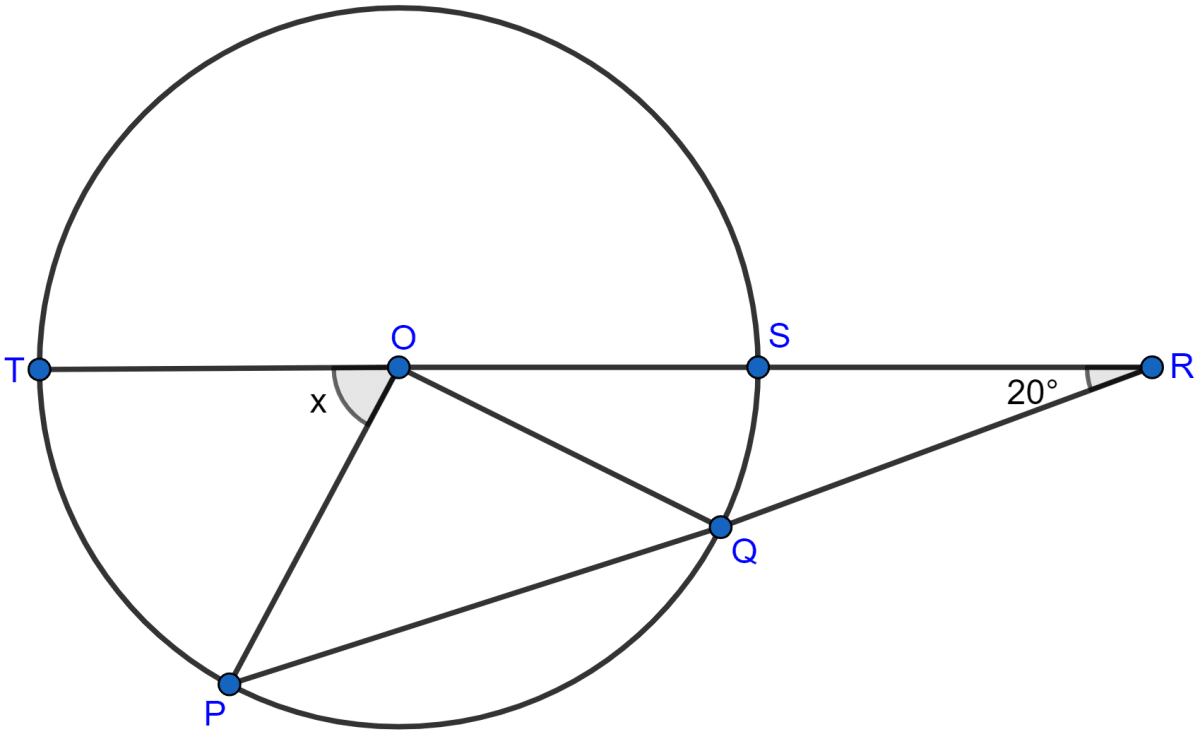
In the adjoining figure, O is the centre of the circle. If QR = OP and ∠ORP = 20°, find the value of 'x' giving reasons.
In the figure (i) given below, triangle ABC is equilateral. Find ∠BDC and ∠BEC.

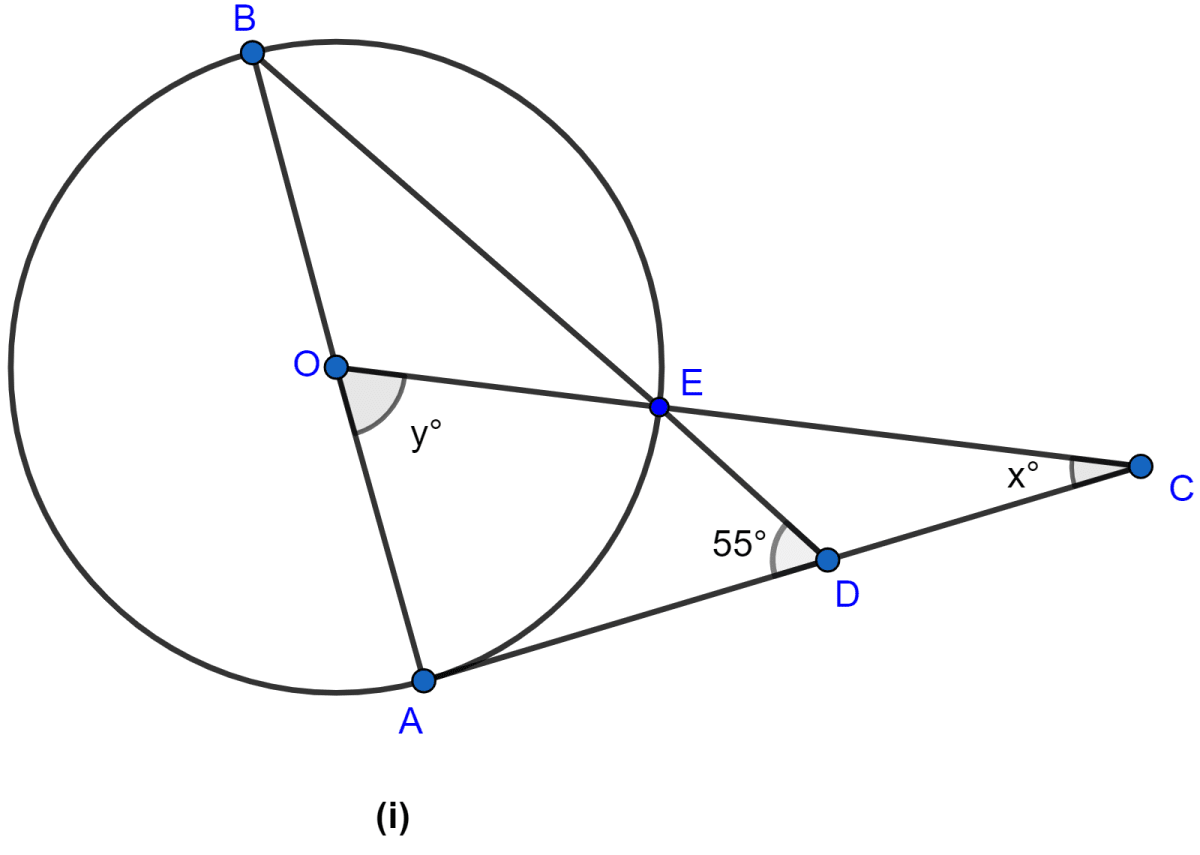
In the figure (i) given below, AC is a tangent to the circle with centre O. If ∠ADB = 55°, find x and y. Give reasons for your answers.
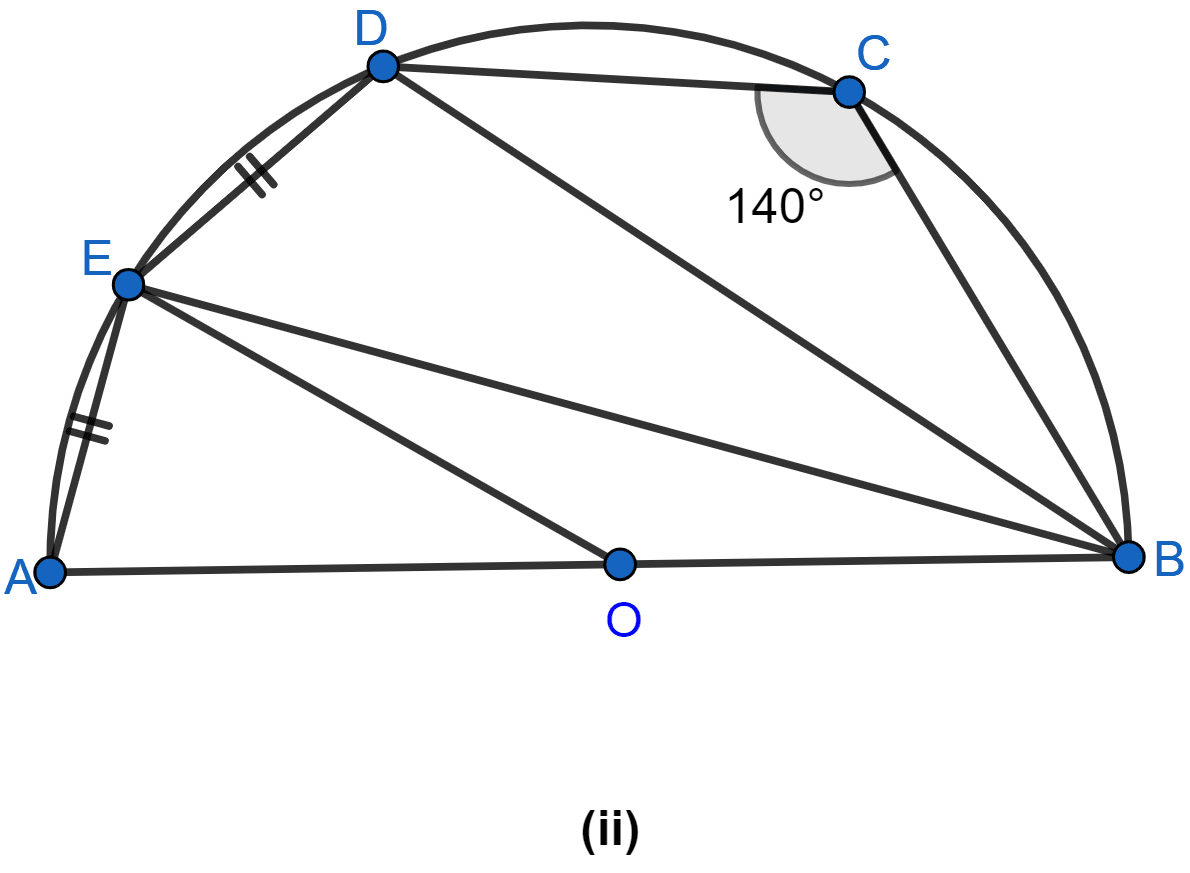
In the figure (ii) given below, AB is a diameter of the semicircle ABCDE with centre O. If AE = ED and ∠BCD = 140°, find ∠AED and ∠EBD. Also prove that OE is parallel to BD.