Mathematics
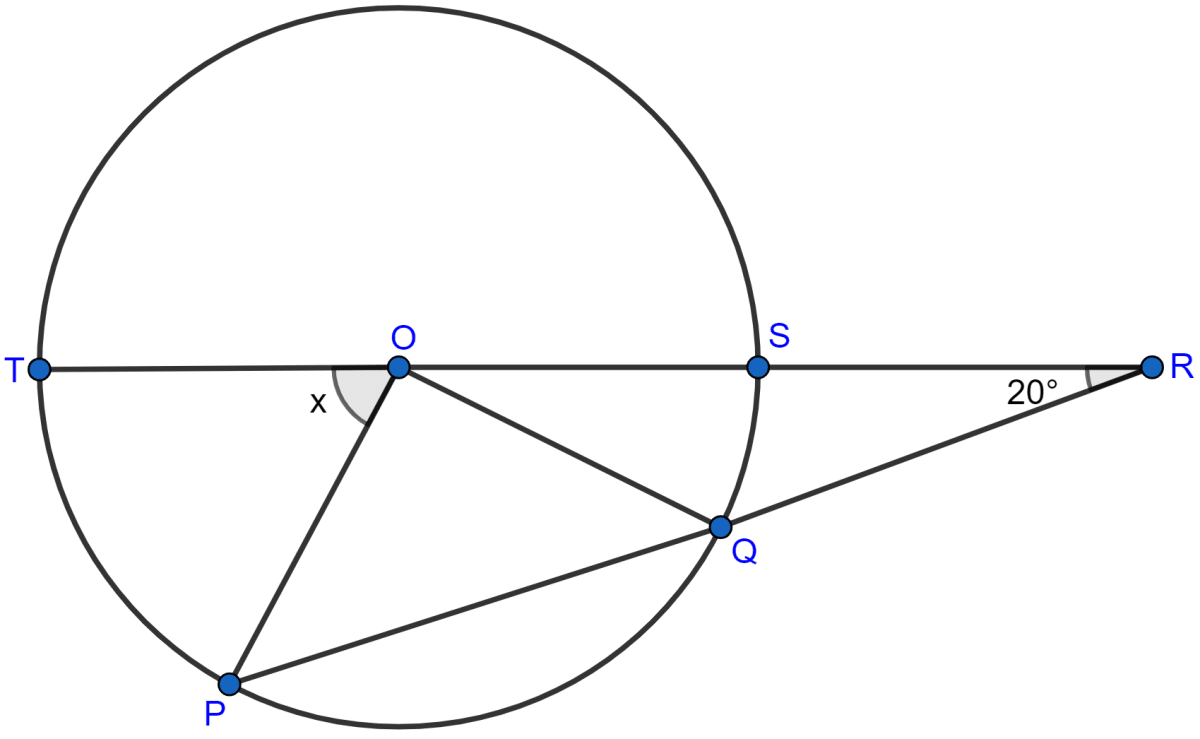
In the adjoining figure, O is the centre of the circle. If QR = OP and ∠ORP = 20°, find the value of 'x' giving reasons.
Circles
23 Likes
Answer
Given,
QR = OP ⇒ QR = OQ
⇒ ∠QOR = ∠ORQ = 20° (∵ angles opposite equal sides of a triangle are equal)
Exterior angle in a triangle is equal to the sum of two opposite interior angles.
∴ ∠OQP = ∠QOR + ∠ORQ = 20° + 20° = 40°.
As OP = OQ, ∠OPQ = ∠OQP
⇒ ∠OPQ = 40°
⇒ ∠OPR = 40°.
Exterior angle in a triangle is equal to the sum of two opposite interior angles.
∴ x = ∠TOP = ∠OPR + ∠ORP = 40° + 20° = 60°.
Hence, the value of x = 60°.
Answered By
15 Likes
Related Questions
In the adjoining figure, PQR is a tangent at Q to a circle. If AB is a chord parallel to PR and ∠BQR = 70°, then ∠AQB is equal to
20°
40°
35°
45°

Two chords AB and CD of a circle intersect externally at a point P. If PC = 15 cm, CD = 7 cm and AP = 12 cm, then AB is
2 cm
4 cm
6 cm
none of these

In the figure (i) given below, triangle ABC is equilateral. Find ∠BDC and ∠BEC.

In the figure (ii) given below, AB is a diameter of a circle with centre O. OD is perpendicular to AB and C is a point on the arc DB. Find ∠BAD and ∠ACD.