Mathematics
Two chords AB and CD of a circle intersect externally at a point P. If PC = 15 cm, CD = 7 cm and AP = 12 cm, then AB is
2 cm
4 cm
6 cm
none of these

Circles
18 Likes
Answer
We know that if two chords of a circle intersect internally or externally, then the products of the lengths of segments are equal.
Hence, from figure,
PA.PB = PC.PD …..(i)
Given,
PC = 15 cm and CD = 7 cm
From figure,
PD = PC - CD = 15 - 7 = 8 cm.
Let BP = x cm then AB = (12 - x) cm
Putting values in equation (i),
⇒ PA.PB = PC.PD
⇒ 12.x = 15.8
⇒ 12x = 120
⇒ x = = 10 cm.
AB = 12 - x = 12 - 10 = 2 cm.
Hence, Option 1 is the correct option.
Answered By
7 Likes
Related Questions
In the adjoining figure, if sides PQ, QR, RS and SP of a quadrilateral PQRS touch a circle at points A, B, C and D respectively, then PD + BQ is equal to
PQ
QR
PS
SR

In the adjoining figure, PQR is a tangent at Q to a circle. If AB is a chord parallel to PR and ∠BQR = 70°, then ∠AQB is equal to
20°
40°
35°
45°

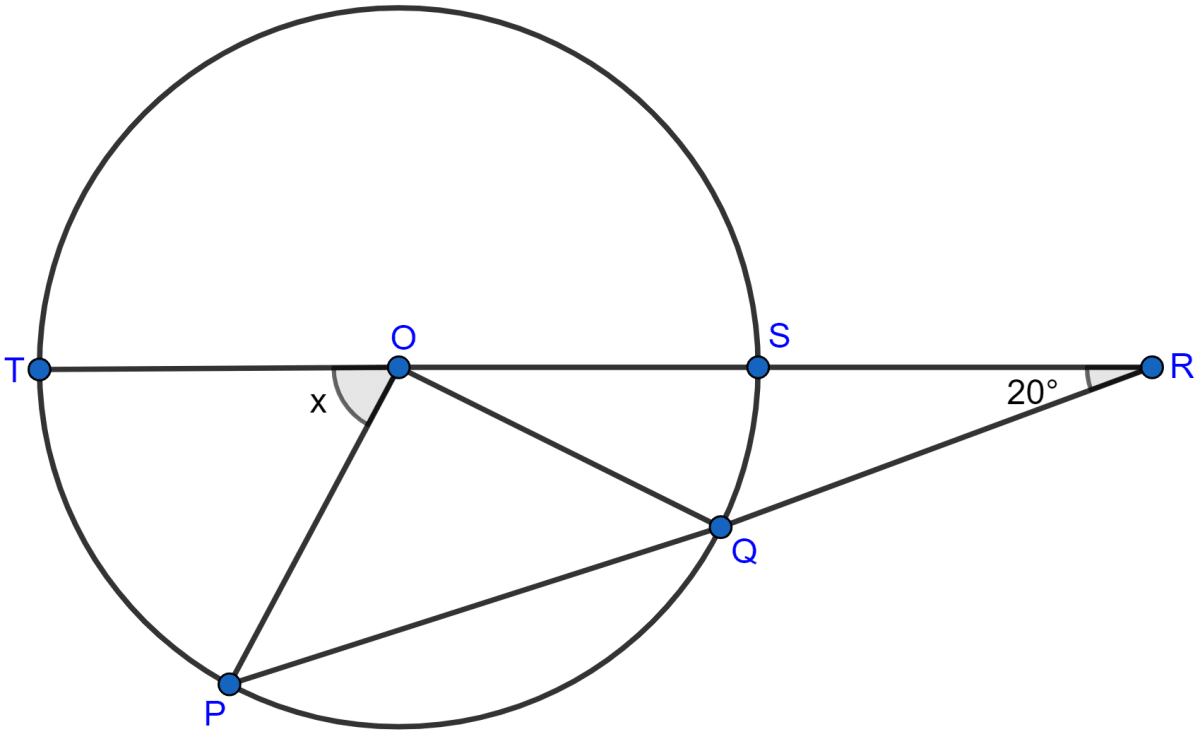
In the adjoining figure, O is the centre of the circle. If QR = OP and ∠ORP = 20°, find the value of 'x' giving reasons.
In the figure (i) given below, triangle ABC is equilateral. Find ∠BDC and ∠BEC.
