Mathematics
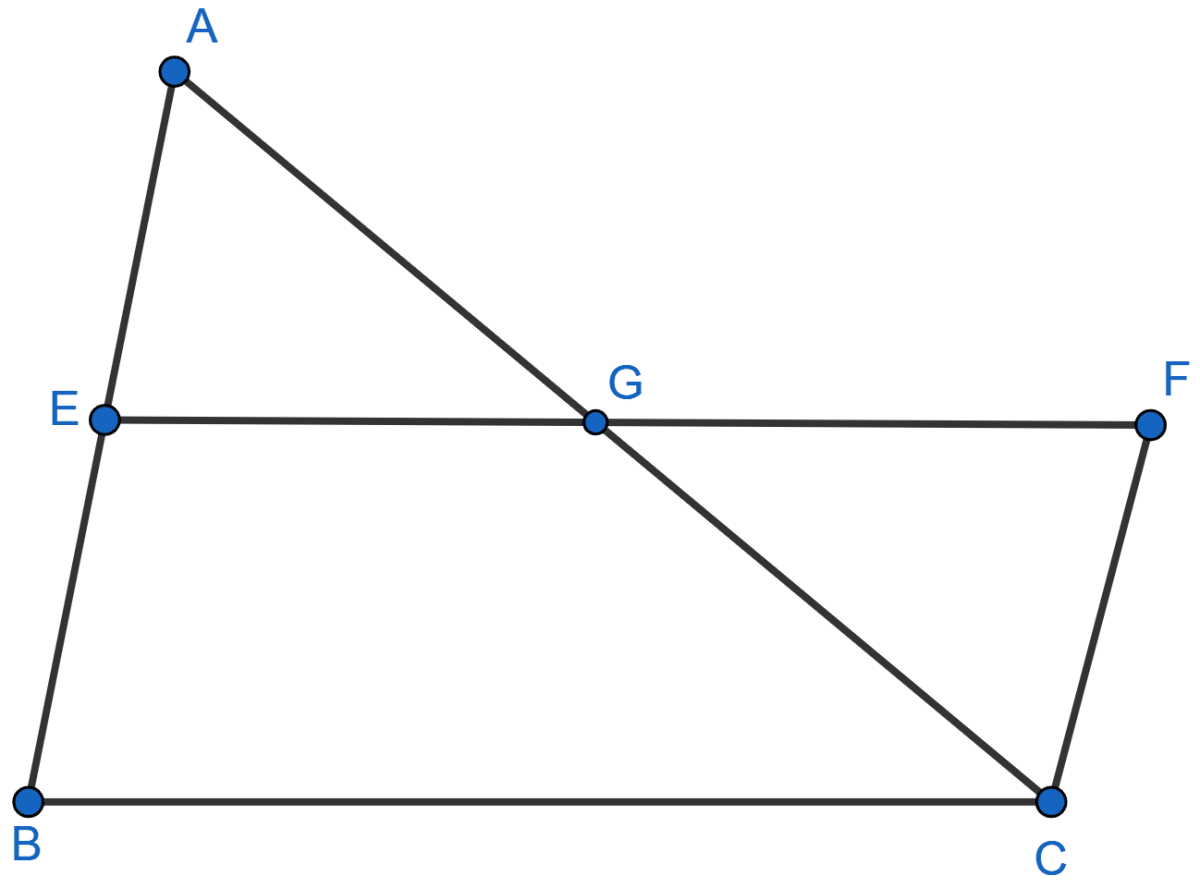
In the adjoining figure, E is the midpoint of the side AB of a triangle ABC and EBCF is a parallelogram. If the area of ∆ ABC is 25 sq. units, find the area of || gm EBCF.
Theorems on Area
19 Likes
Answer
In △ABC,
As E is mid-point of AB and EF || BC so,
G is mid-point of AC (By mid-point theorem)
∴ AG = GC.
In ∆AEG and ∆CFG,
∠EAG = ∠GCF (Alternate angles are equal)
∠EGA = ∠CGF (Vertically opposite angles are equal)
AG = GC (Proved above)
Hence, ∆AEG ≅ ∆CFG (By ASA axiom)
∴ area of ∆AEG = area of ∆CFG ……….(i)
From figure,
area of || gm EBCF = area of quad. BCGE + area of ∆CFG
= area of quad. BCGE + area of ∆AEG ……..(from i)
= area of ∆ABC = 25 sq. units.
Hence, area of ||gm EBCF = 25 sq. units.
Answered By
8 Likes
Related Questions
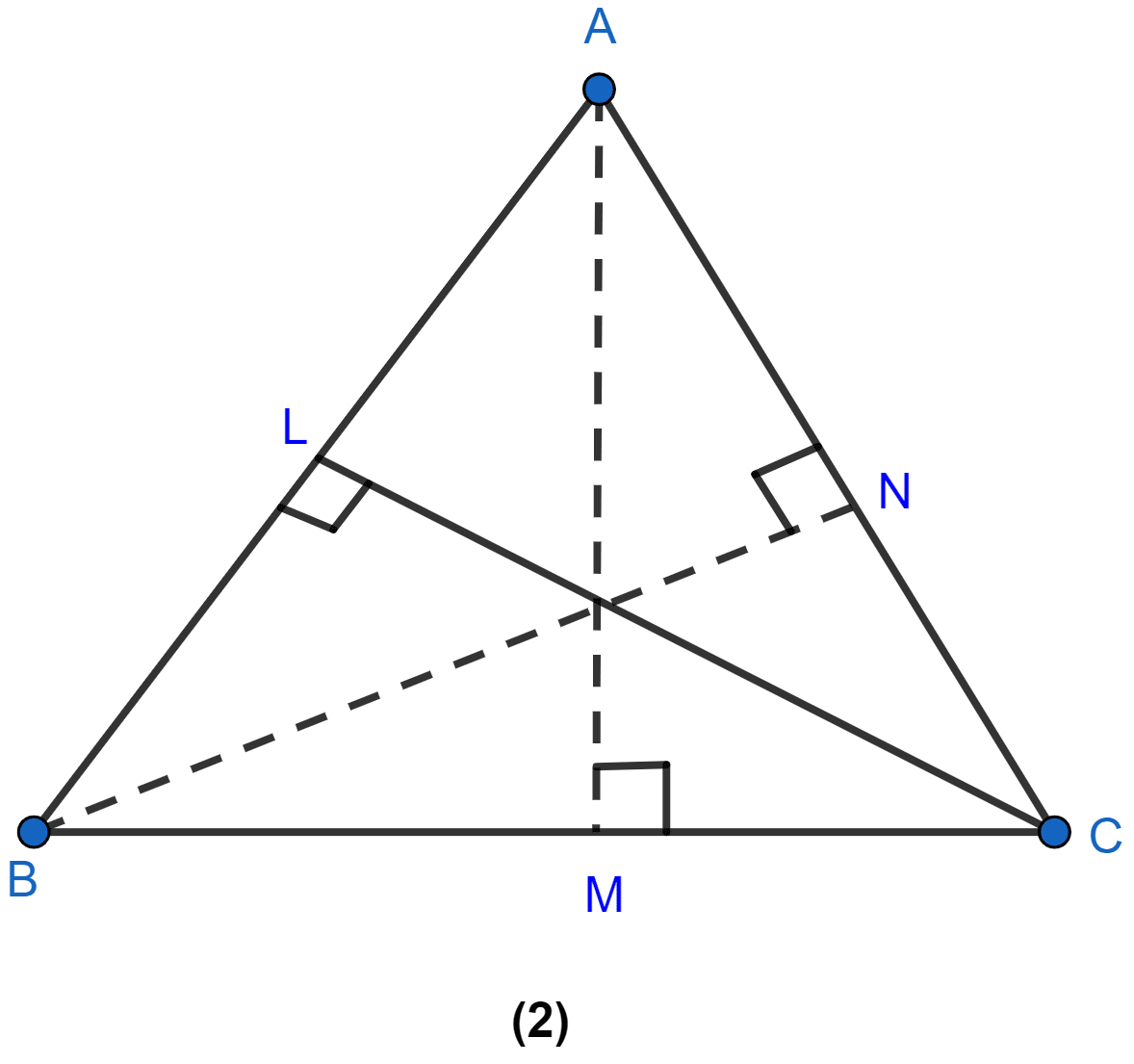
In the figure (2) given below, the perimeter of ∆ABC is 37 cm. If the lengths of the altitudes AM, BN and CL are 5x, 6x, and 4x respectively, calculate the lengths of the sides of ∆ABC.
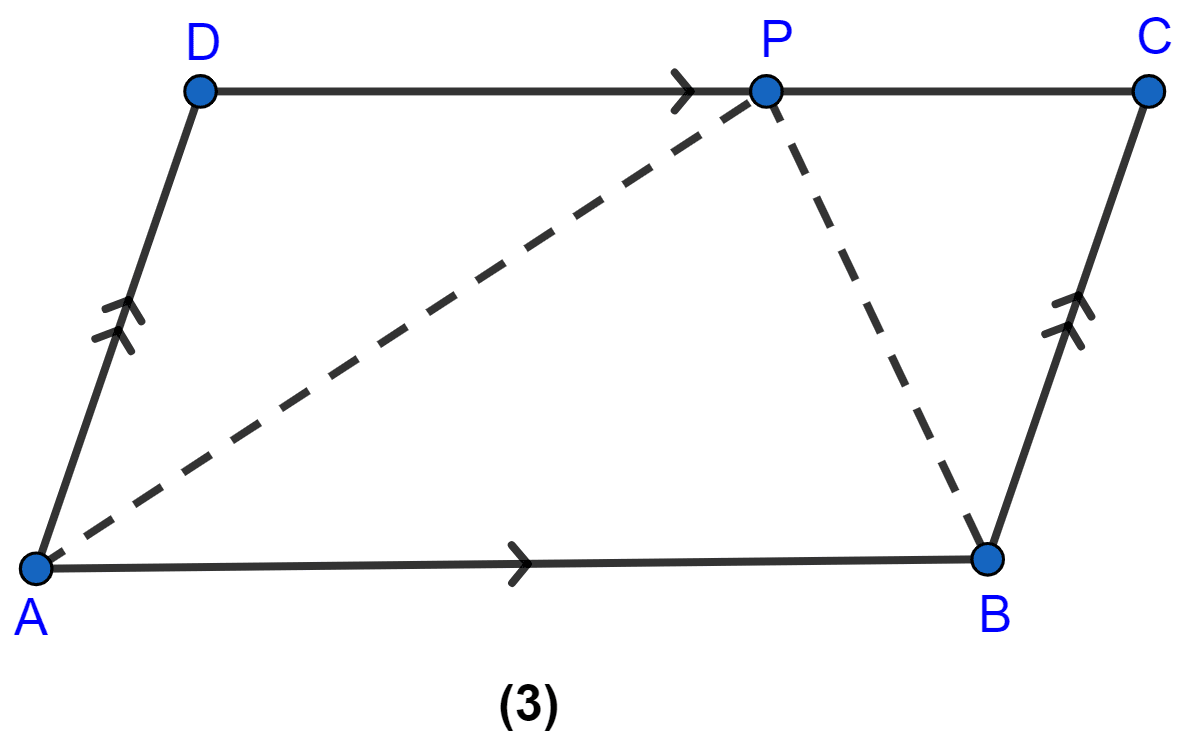
In the figure(3) given below, ABCD is a parallelogram. P is a point on DC such that area of ∆DAP = 25 cm2 and the area of ∆BCP = 15 cm2. Find
(i) area of || gm ABCD
(ii) DP : PC.
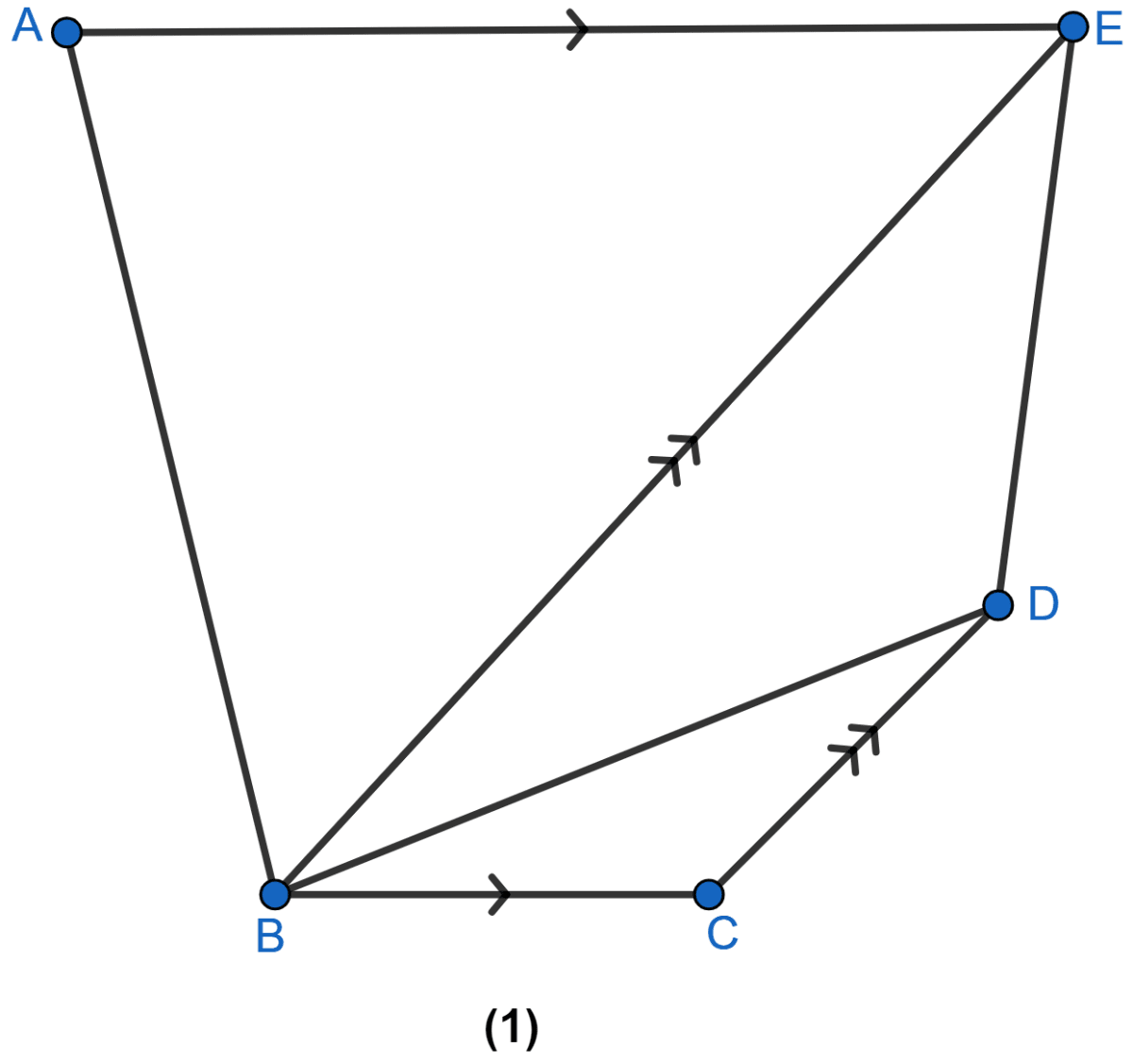
In the figure (1) given below, BC || AE and CD || BE. Prove that
area of ∆ABC= area of ∆EBD.
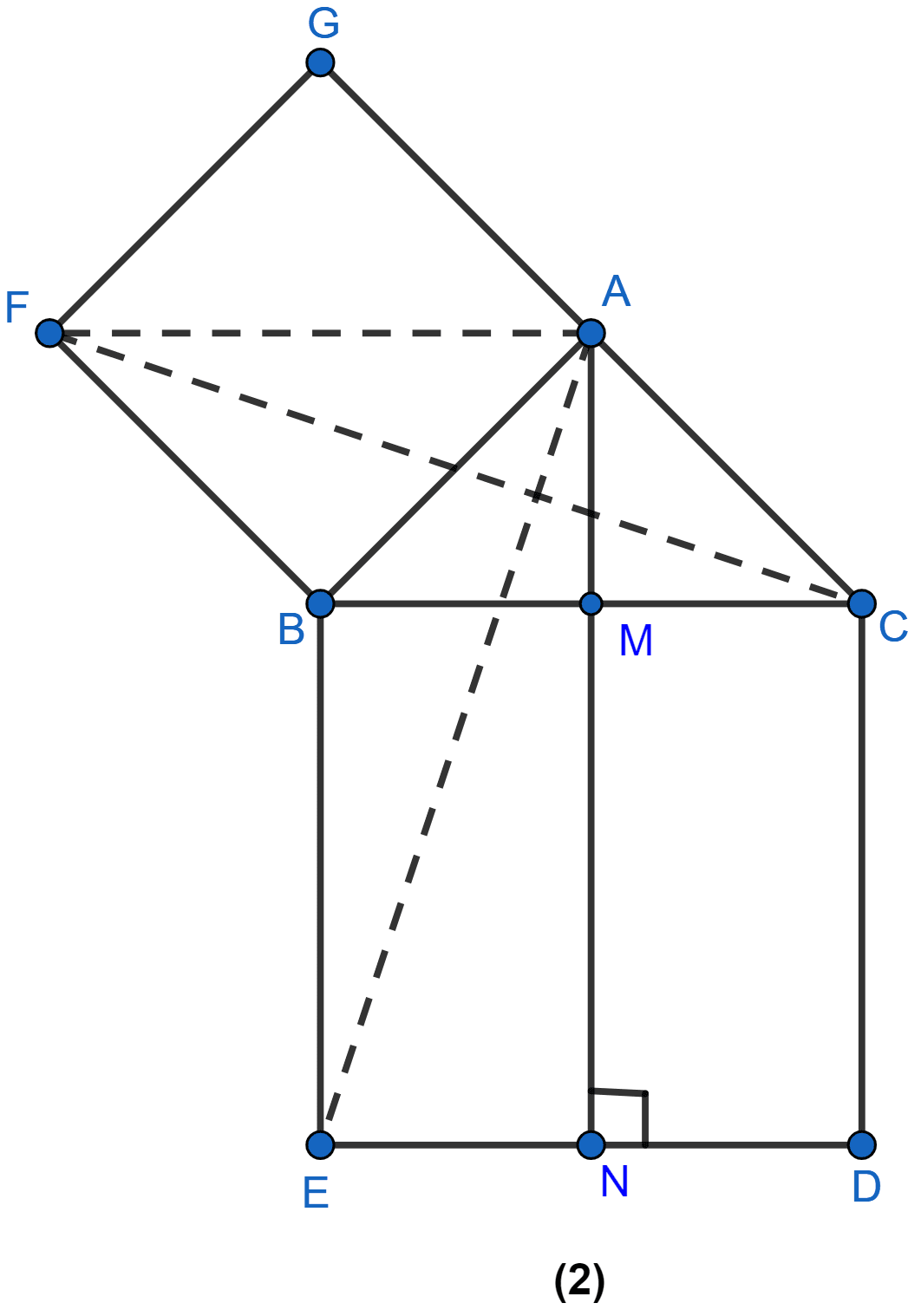
In figure (2) given below, ABC is a right-angled triangle at A. AGFB is a square on the side AB and BCDE is a square on the hypotenuse BC. If AN ⊥ ED, prove that
(i) ∆BCF ≅ ∆ABE.
(ii) area of square ABFG = area of rectangle BENM.