Mathematics
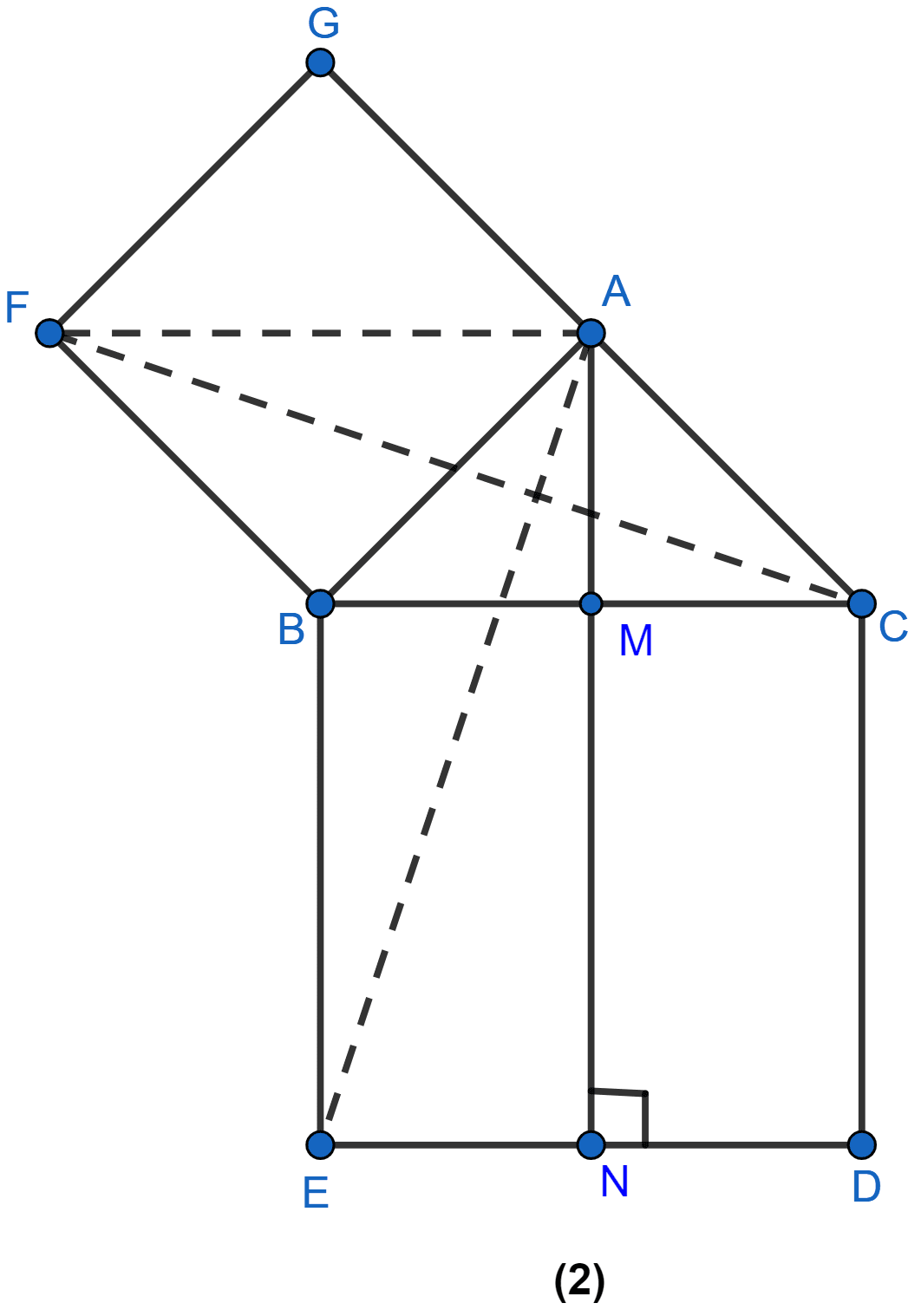
In figure (2) given below, ABC is a right-angled triangle at A. AGFB is a square on the side AB and BCDE is a square on the hypotenuse BC. If AN ⊥ ED, prove that
(i) ∆BCF ≅ ∆ABE.
(ii) area of square ABFG = area of rectangle BENM.
Theorems on Area
31 Likes
Answer
(i) From figure,
⇒ ∠FBC = ∠FBA + ∠ABC
∠FBA = 90° (As each angle of a square = 90°)
⇒ ∠FBC = 90° + ∠ABC ……. (1)
Also,
⇒ ∠ABE = ∠CBE + ∠ABC
∠CBE = 90° (As each angle of a square = 90°)
⇒ ∠ABE = 90° + ∠ABC …….(2)
From (1) and (2), we get
∠FBC = ∠ABE …….. (3)
Now, in ∆BCF and ∆ABE
BF = AB (As FBAG is a square)
∠FBC = ∠ABE (Proved above)
BC = BE (As BCDE is a square)
By using the SAS axiom rule of congruency,
∴ ∆BCF ≅ ∆ ABE.
Hence, proved that ∆BCF ≅ ∆ ABE.
(ii) We know that,
∆BCF ≅ ∆ABE
So, area of ∆BCF = area of ∆ABE …… (4)
Since, ∆BCF and square AGFB have same base FB and are between same parallel lines FB and GC.
area of ∆BCF = area of square AGFB ……..(5)
∆ABE and rectangle BENM are on same base BE and are between same parallel lines BE and AN.
area of ∆ABE = area of rectangle BENM ……. (6)
From (4), (5) and (6)
⇒ area of square AGFB = area of rectangle BENM
⇒ area of square AGFB = area of rectangle BENM
Hence, proved that area of square AGFB = area of rectangle BENM.
Answered By
20 Likes
Related Questions
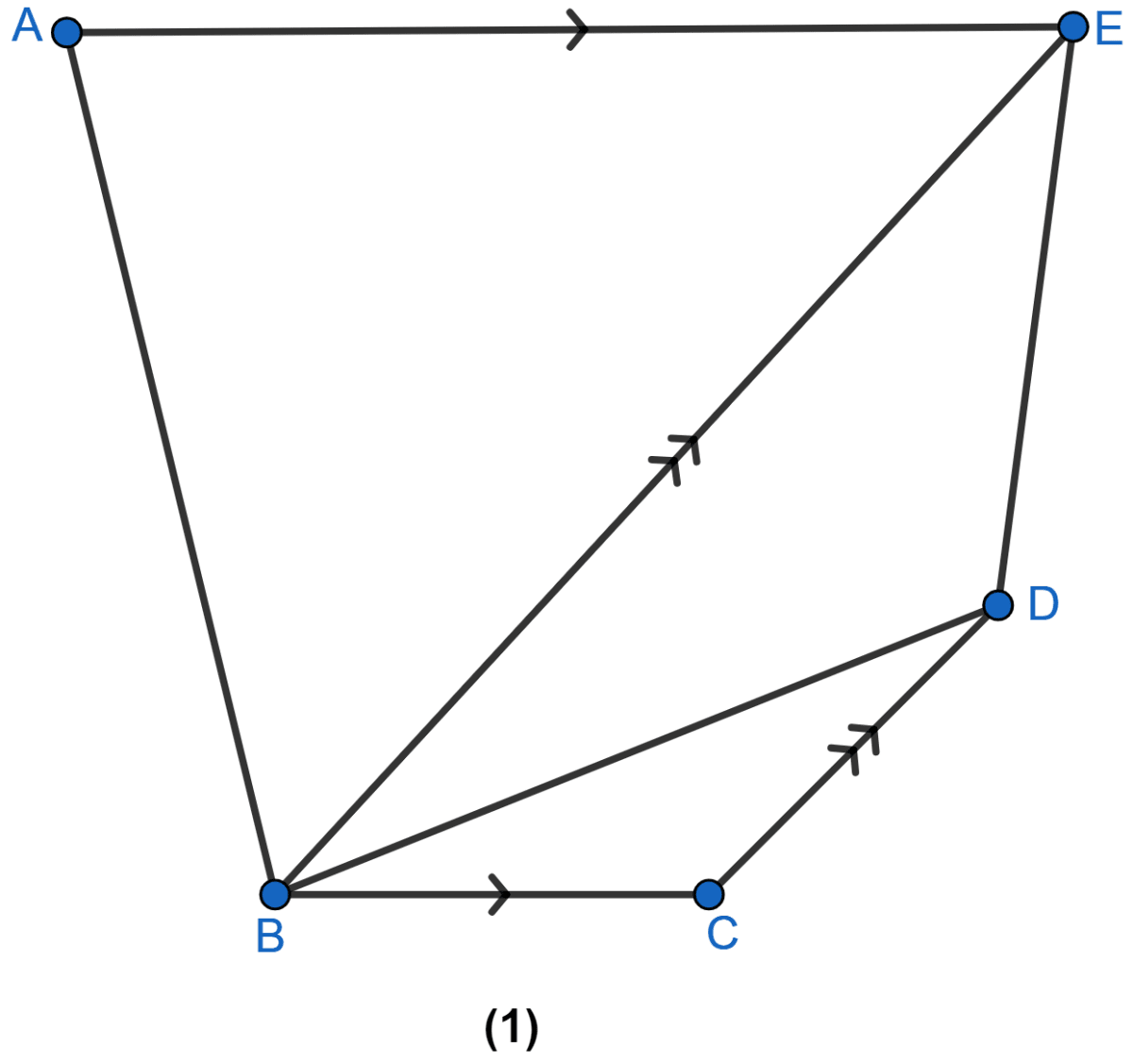
In the adjoining figure, E is the midpoint of the side AB of a triangle ABC and EBCF is a parallelogram. If the area of ∆ ABC is 25 sq. units, find the area of || gm EBCF.
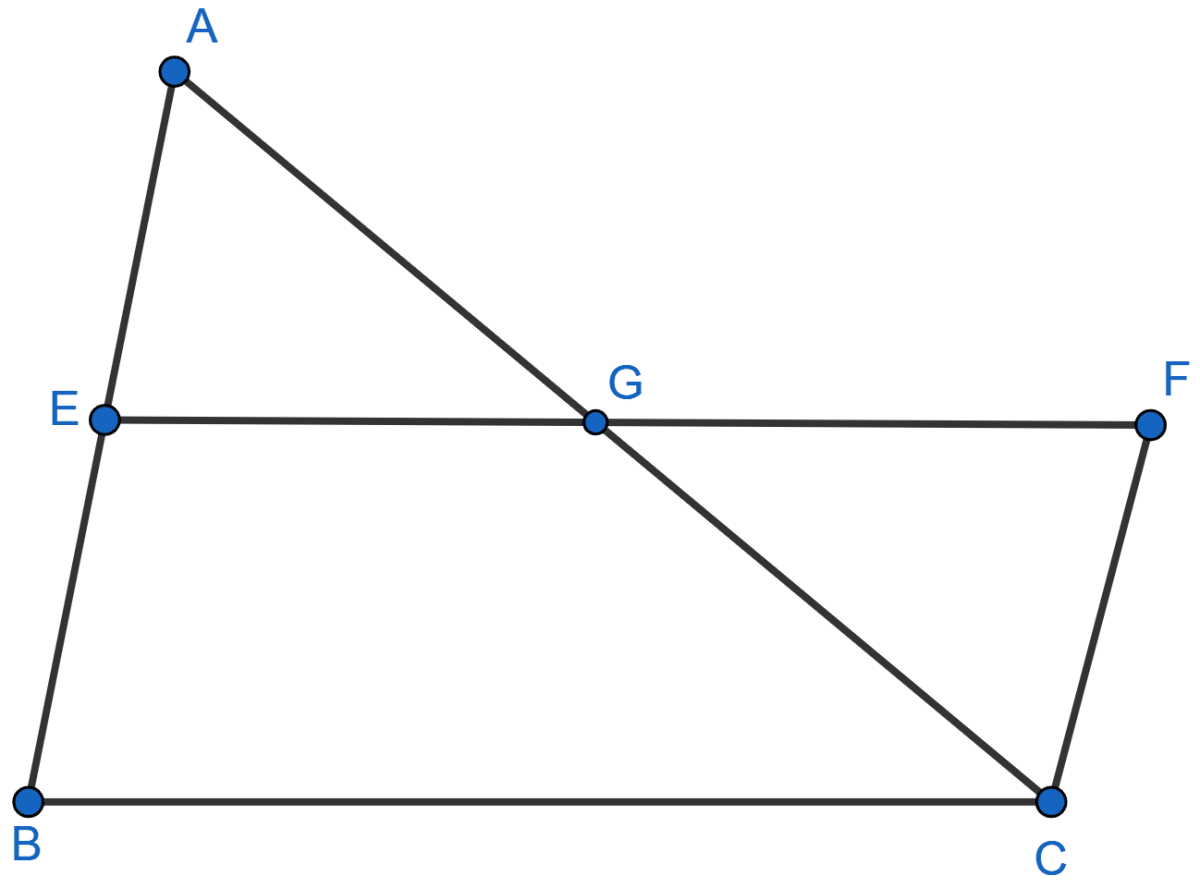
In the figure (1) given below, BC || AE and CD || BE. Prove that
area of ∆ABC= area of ∆EBD.
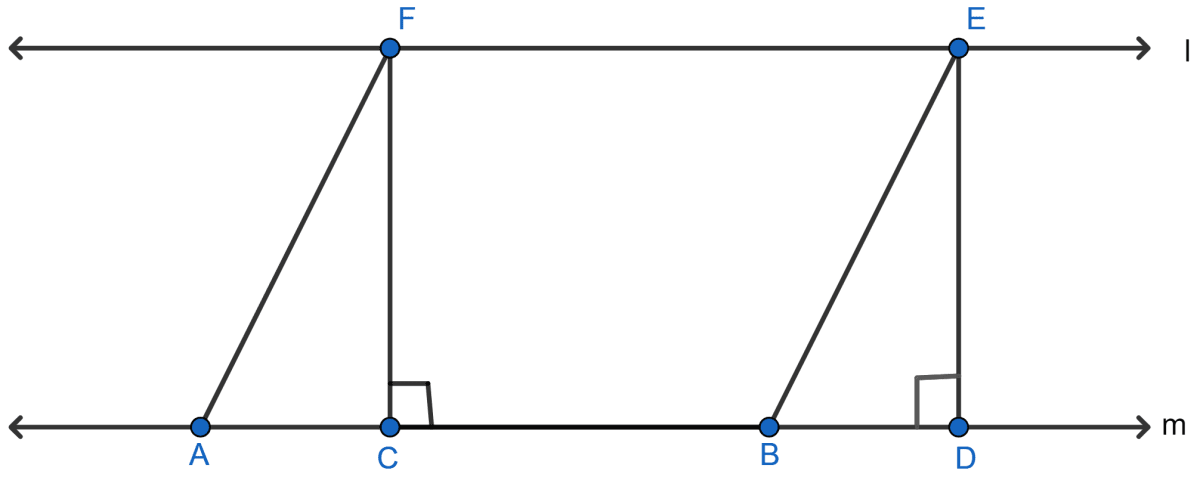
In the adjoining figure, if l || m, AF || BE, FC ⊥ m and ED ⊥ m, then the correct statement is
area of || ABEF = area of rect. CDEF
area of || ABEF = area of quad. CBEF
area of || ABEF = 2 area of △ACF
area of || ABEF = 2 area of △EBD
Two parallelograms are on equal bases and between the same parallels. The ratio of their areas is
1 : 2
1 : 1
2 : 1
3 : 1