Mathematics
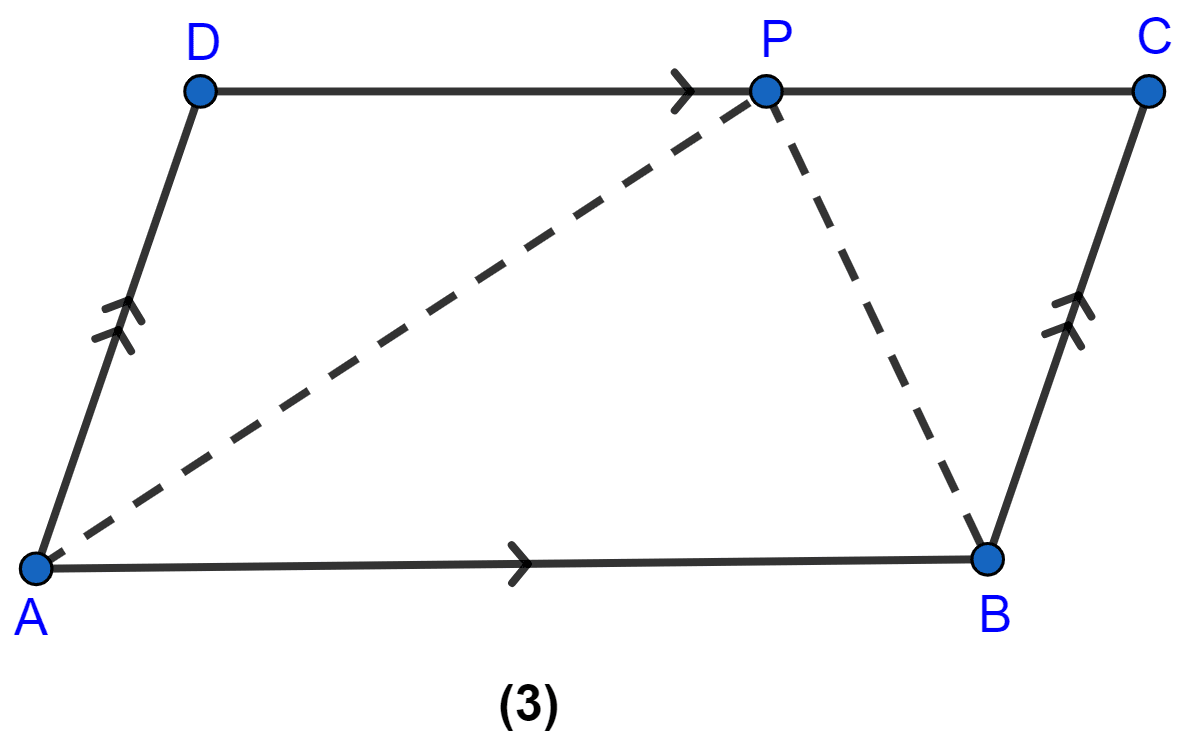
In the figure(3) given below, ABCD is a parallelogram. P is a point on DC such that area of ∆DAP = 25 cm2 and the area of ∆BCP = 15 cm2. Find
(i) area of || gm ABCD
(ii) DP : PC.
Theorems on Area
22 Likes
Answer
(i) Since,
∆APB and || gm ABCD have same base AB and are between same parallel lines AB and DC. So,
area of ∆APB = area of ||gm ABCD
From figure,
⇒ area of ||gm ABCD = area of (∆DAP + ∆BCP)
⇒ area of ||gm ABCD = 25 + 15 = 40
⇒ area of ||gm ABCD = 2 × 40 = 80 cm2.
Hence, area of ||gm ABCD = 80 cm2.
(ii) From figure,
∆DAP and ∆BCP are on the same base CD and between the same parallel lines CD and AB.
Hence, DP : PC = 5 : 3.
Answered By
15 Likes
Related Questions
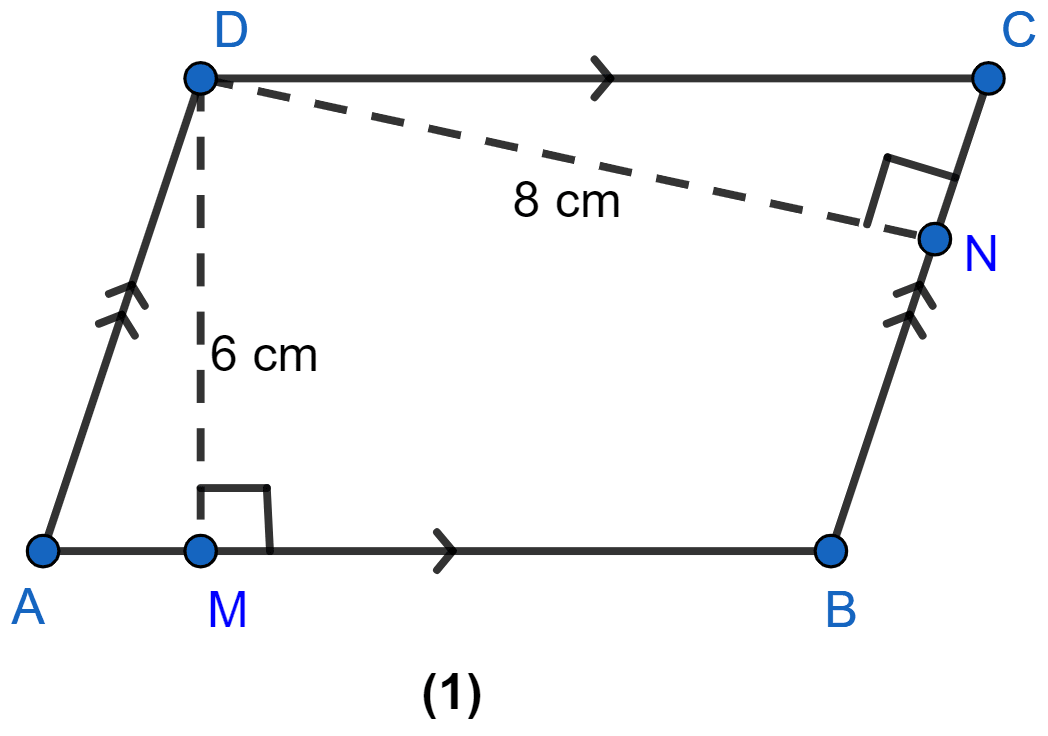
In figure (1) given below, the perimeter of the parallelogram is 42 cm. Calculate the lengths of the sides of the parallelogram.
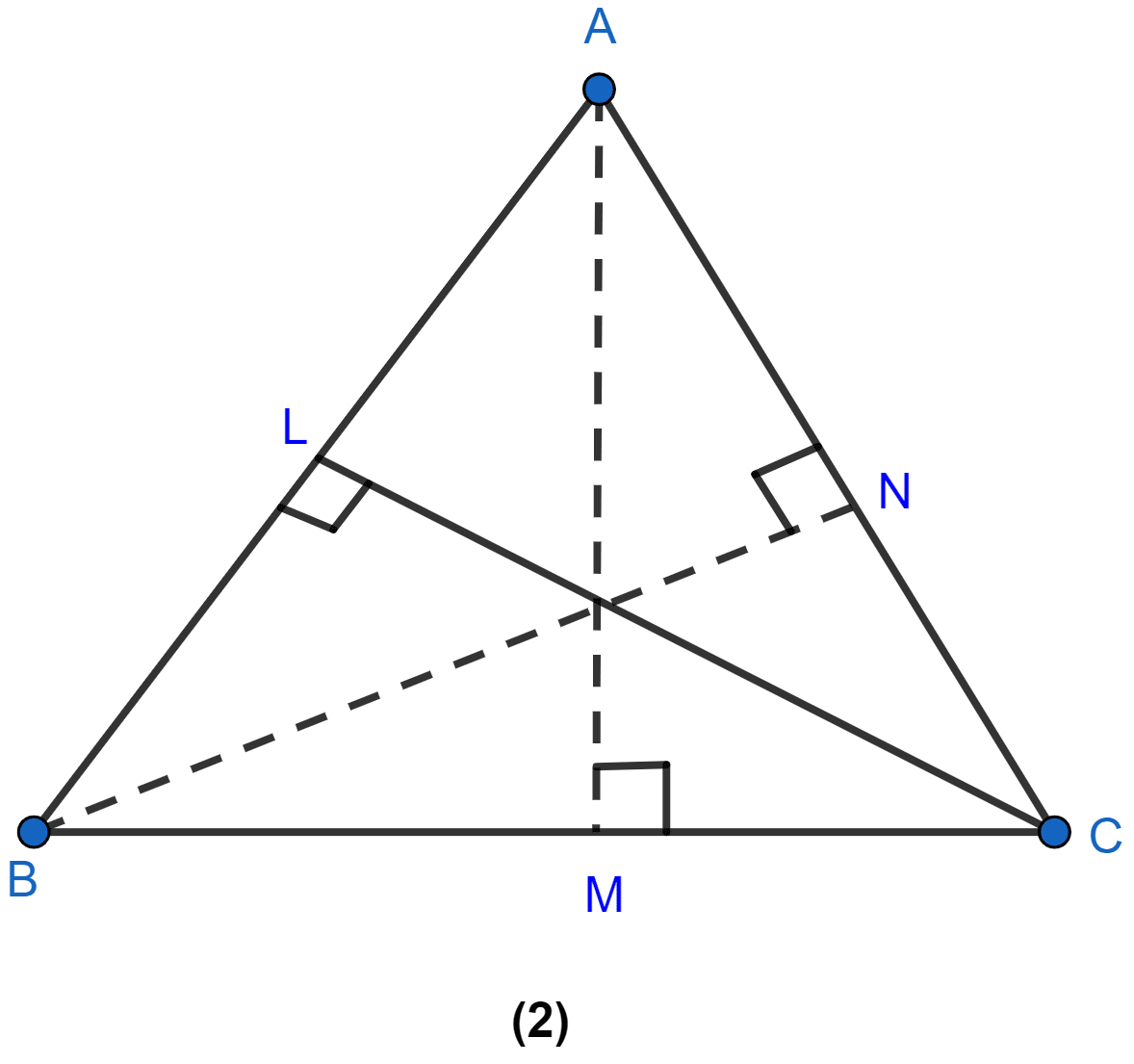
In the figure (2) given below, the perimeter of ∆ABC is 37 cm. If the lengths of the altitudes AM, BN and CL are 5x, 6x, and 4x respectively, calculate the lengths of the sides of ∆ABC.
In the adjoining figure, E is the midpoint of the side AB of a triangle ABC and EBCF is a parallelogram. If the area of ∆ ABC is 25 sq. units, find the area of || gm EBCF.
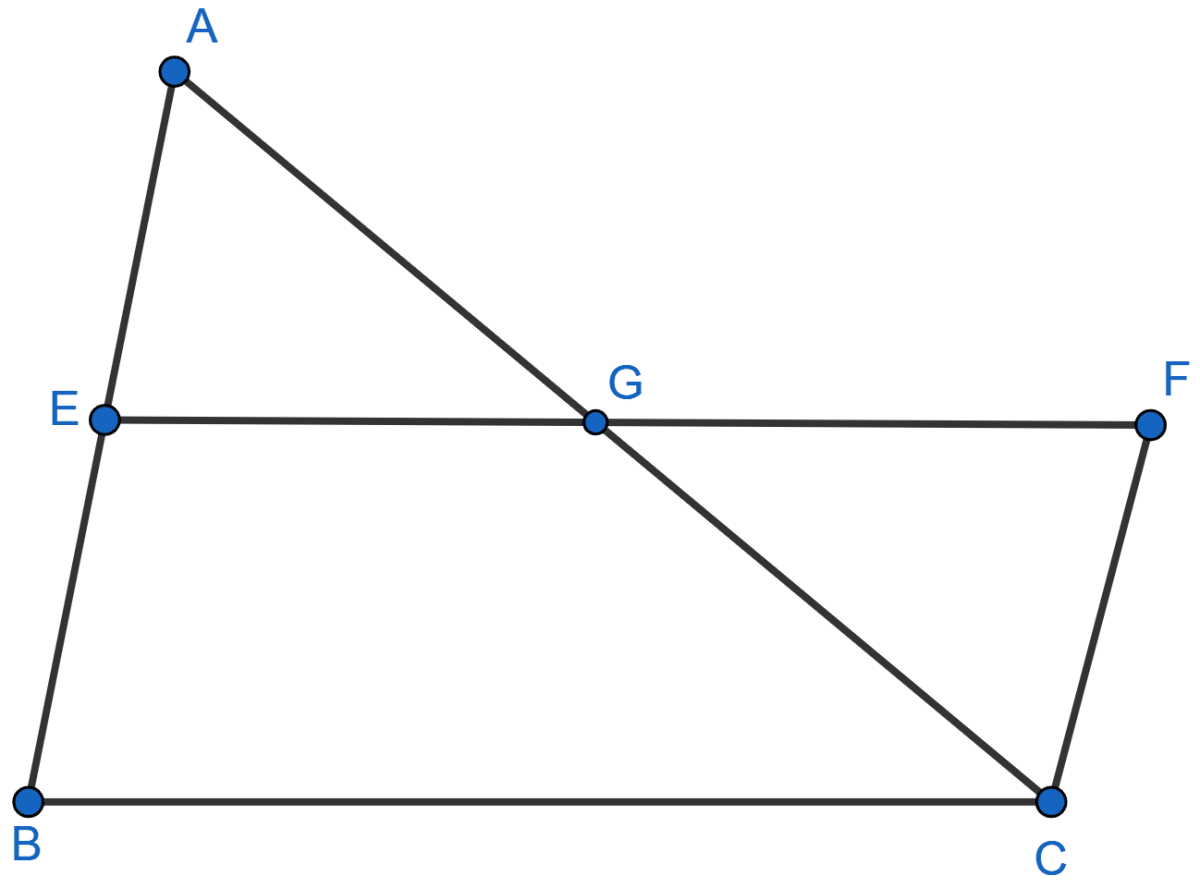
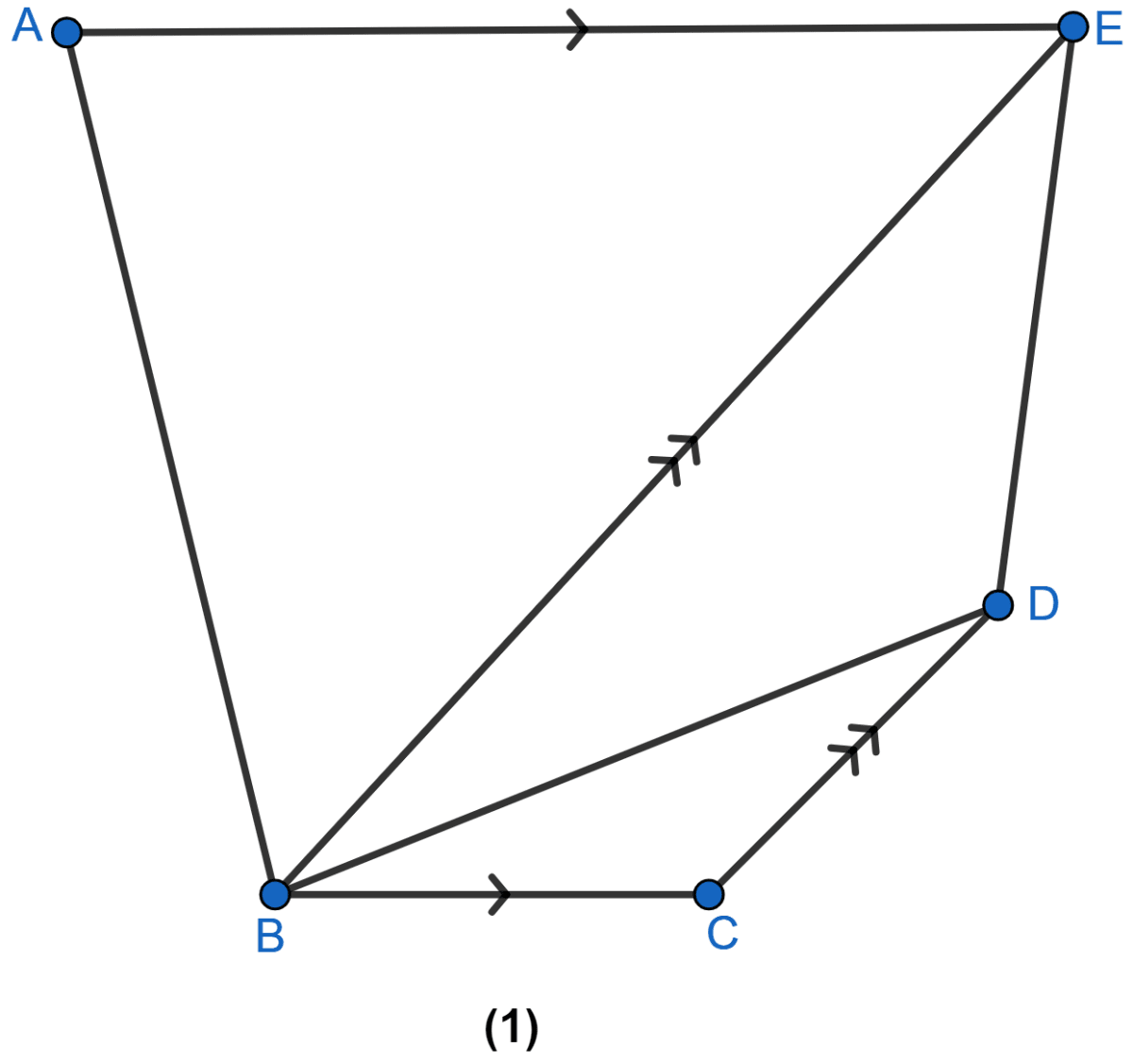
In the figure (1) given below, BC || AE and CD || BE. Prove that
area of ∆ABC= area of ∆EBD.