Mathematics
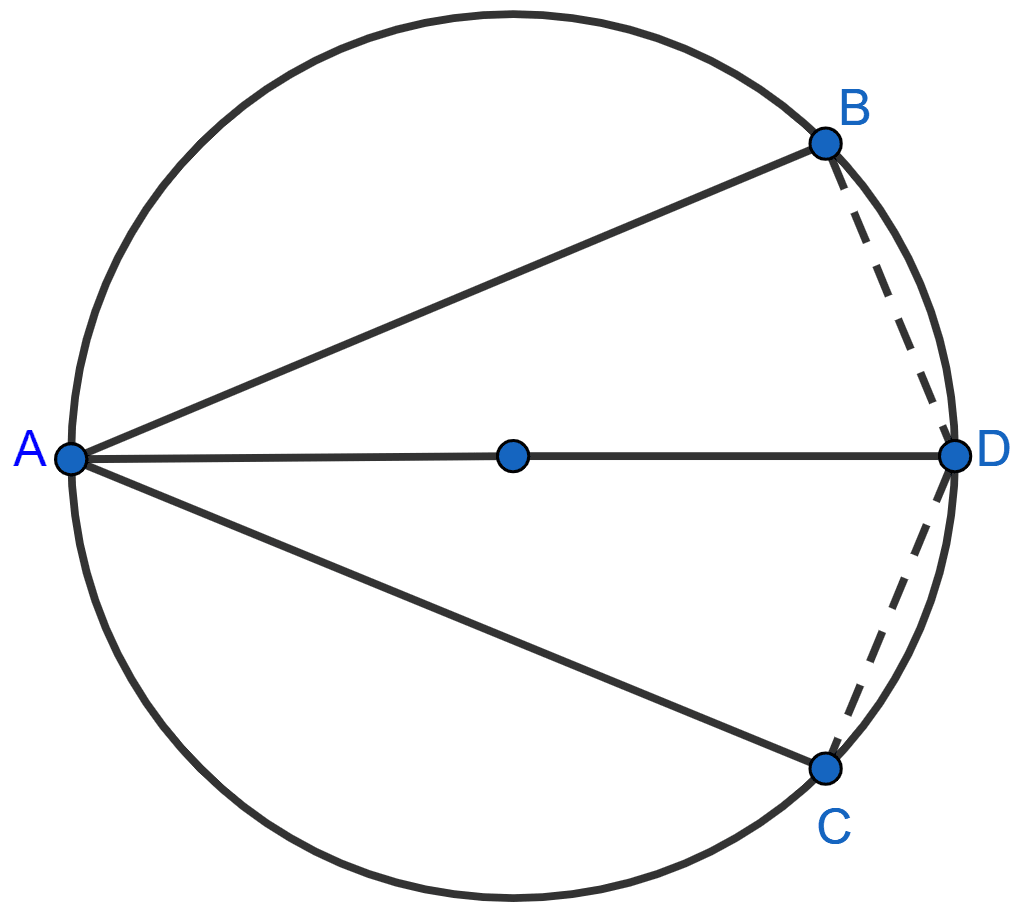
In the adjoining figure, AD is diameter of a circle. If the chord AB and AC are equidistant from its center O, prove that AD bisects ∠BAC and ∠BDC.
Answer
As chords AB and AC are equidistant from the center, so AB = AC. [∵ equal chords are equidistant from center]
Since, angle in a semicircle = 90°.
∠B = ∠C
In △ABD and △ACD,
∠B = ∠C (Both equal to 90°)
AD = AD (Common)
AB = AC (Proved above)
∴ △ABD ≅ △ACD (By R.H.S. congruence rule).
∴ ∠BAD = ∠CAD and ∠BDA = ∠CDA (By C.P.C.T.)
Hence, proved that AD bisects ∠BAC and ∠BDC.
Related Questions
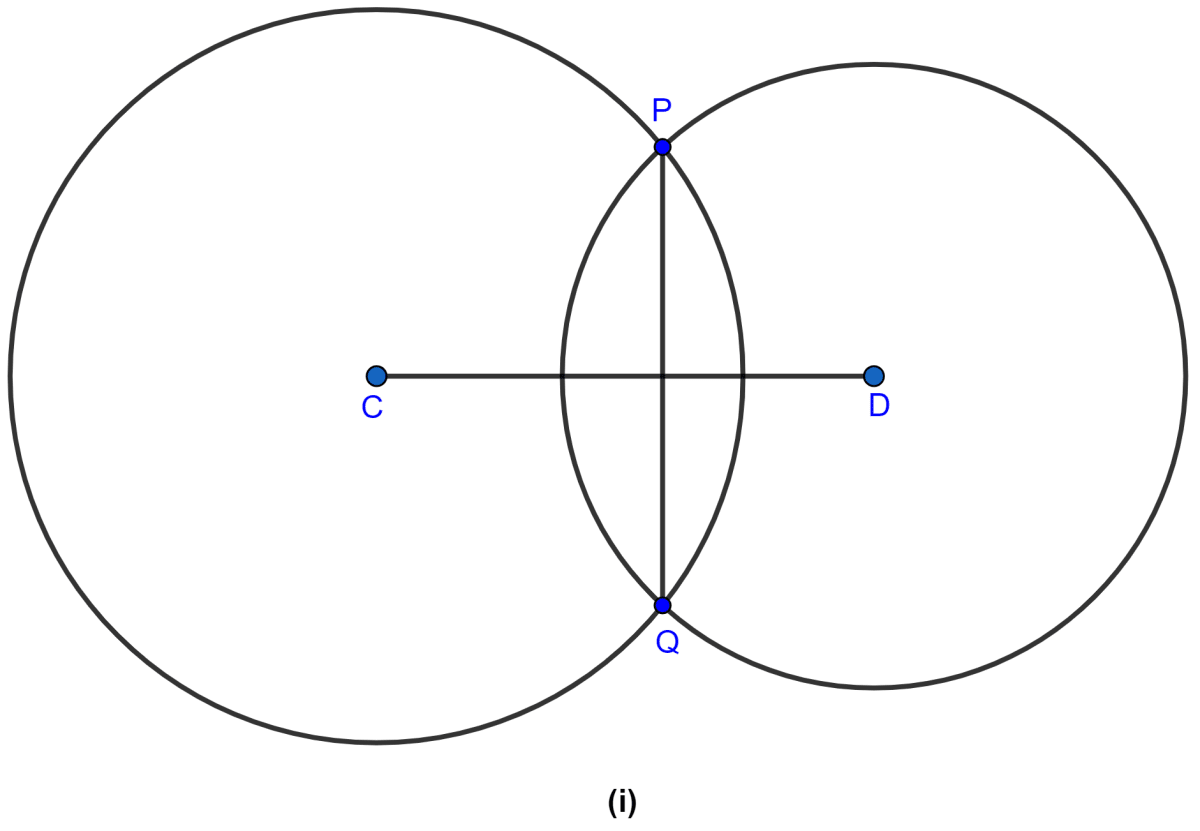
In the figure (i) given below, two circles with centers C, D intersect in points P, Q. If length of common chord is 6 cm and CP = 5 cm, DP = 4 cm, calculate the distance CD correct to two decimal places.
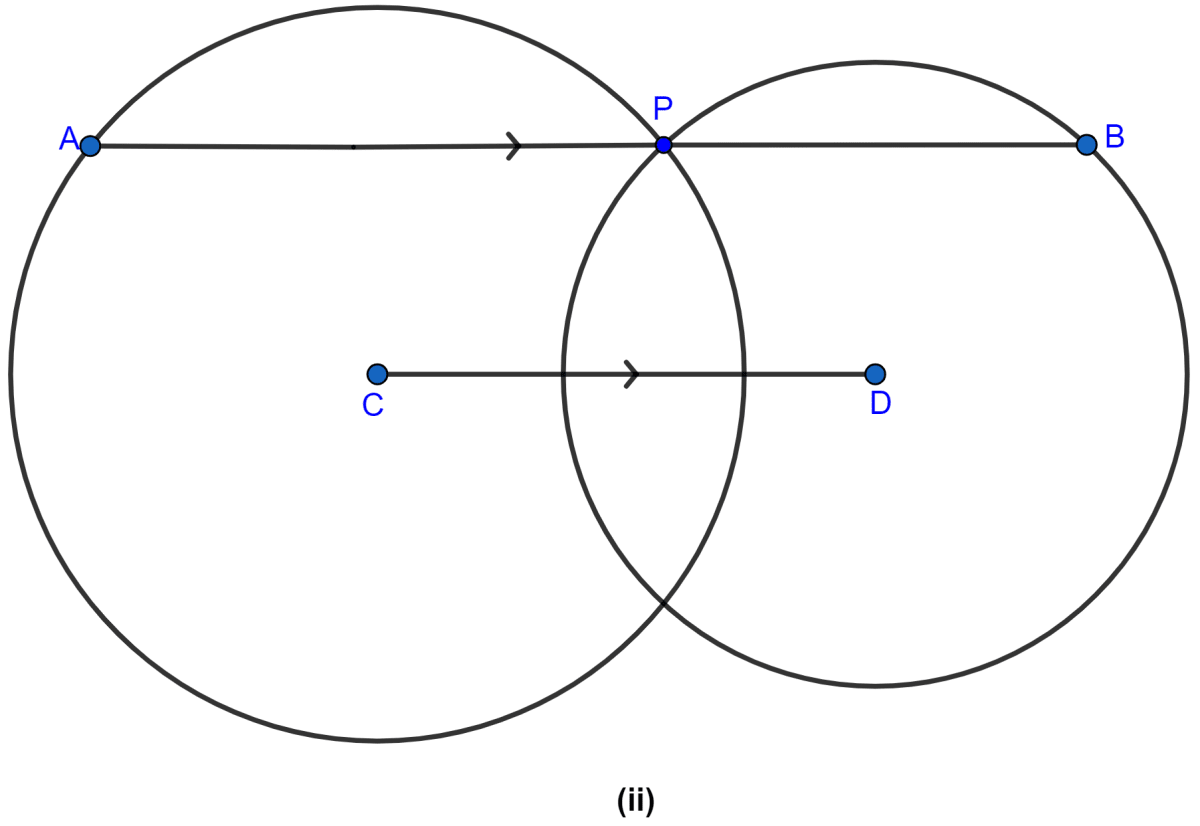
In the figure (ii) given below, P is a point of intersection of two circles with centers C and D. If the st. line APB is parallel to CD, prove that AB = 2CD.
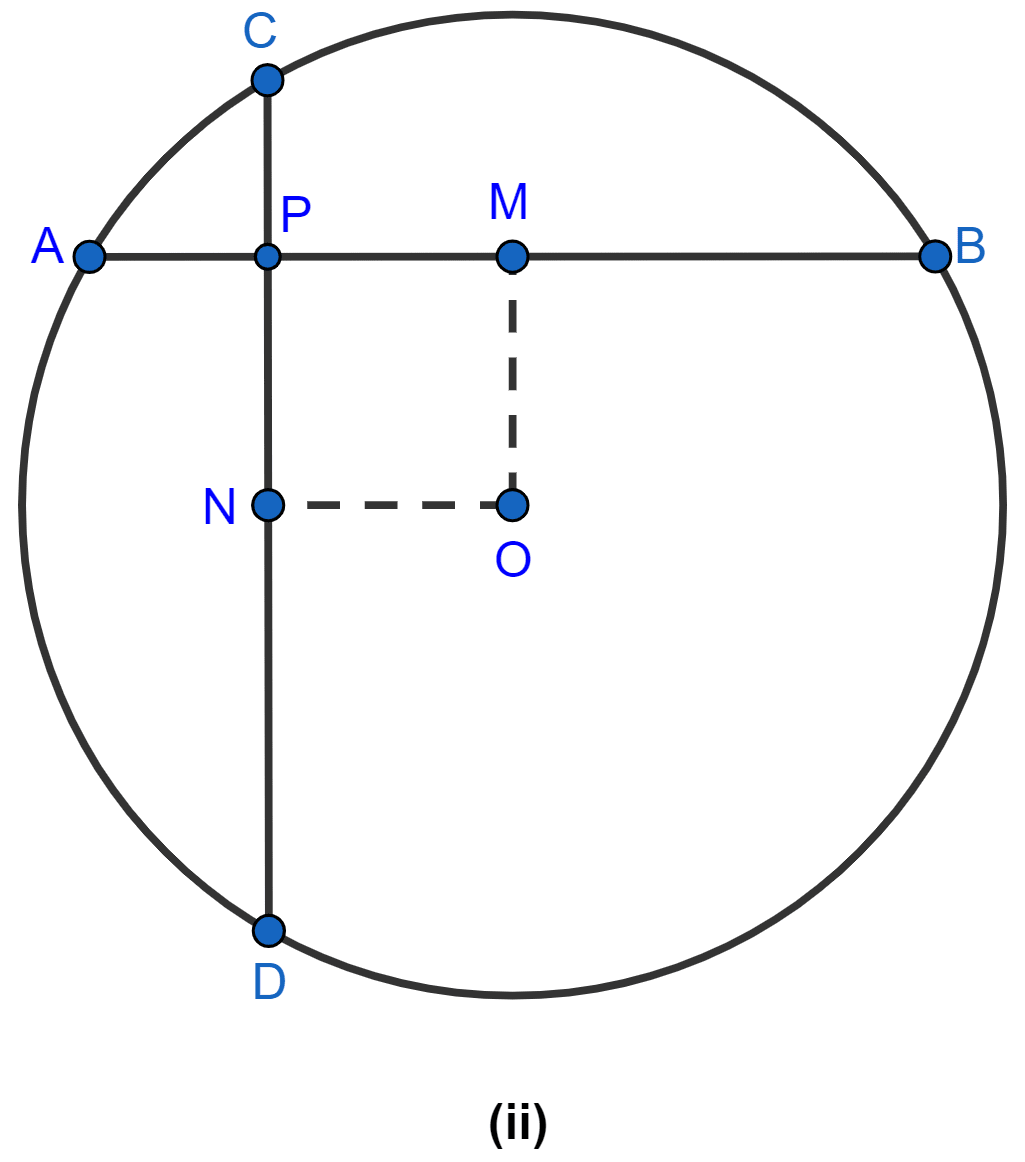
In the figure (i) given below, C and D are centers of two intersecting circles. The line APQB is perpendicular to the line of centers CD. Prove that
(i) AP = QB
(ii) AQ = BP.

In the figure (ii) given below, two equal chords AB and CD of a circle with center O intersect at right angles at P. If M and N are mid-points of the chords AB and CD respectively, prove that NOMP is a square.